Параллельное соединение элементов

Системой с параллельным соединением элементов называется система, отказ которой происходит только в случае отказа всех ее элементов (см. п. 2, рис. 2.2). Такие схемы надежности характерны для ТС, в которых элементы дублируются или резервируются, т.е. параллельное соединение используется как метод повышения надежности (см. п. 4.2). Однако такие системы встречаются и самостоятельно (например, системы двигателей четырехмоторного самолета или параллельное включение диодов в мощных выпрямителях).

Для отказа системы с параллельным соединением элементов в течение наработки t необходимо и достаточно, чтобы все ее элементы отказали в течение этой наработки. Так что отказ системы заключается в совместном отказе всех элементов, вероятность чего (при допущении независимости отказов) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказа элементов:

(3.7)

Соответственно, вероятность безотказной работы

(3.8)

Для систем из равнонадежных элементов ()

(3.9)

т.е. надежность системы с параллельным соединением повышается при увеличении числа элементов (например, при и , а при ).

Поскольку , произведение в правой части (3.7) всегда меньше любого из сомножителей, т.е. вероятность отказа системы не может быть выше вероятности самого надежного ее элемента (“лучше лучшего”) и даже из сравнительно ненадежных элементов возможно построение вполне надежной системы.

При экспоненциальном распределении наработки (1.7) выражение (3.9) принимает вид

(3.10)

откуда с помощью (1.1) после интегрирования и преобразований средняя наработка системы определяется

(3.11)

где 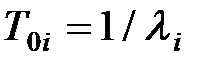- средняя наработка элемента. При больших значениях n справедлива приближенная формула

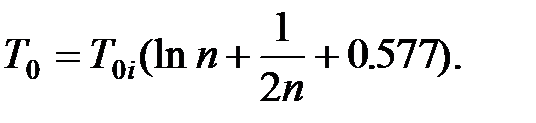(3.12)

Таким образом, средняя наработка системы с параллельным соединением больше средней наработки ее элементов (например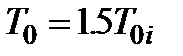, при , при ).

 

 

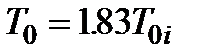8. Системы типа “m из n”. Метод прямого перебора.

Систему типа “m из n” можно рассматривать как вариант системы с параллельным соединением элементов, отказ которой произойдет, если из n элементов, соединенных параллельно, работоспособными окажутся менее m элементов (m < n).

На рис. 3.1 представлена система “2 из 5”, которая работоспособна, если из пяти её элементов работают любые два, три, четыре или все пять Системы типа “m из n” наиболее часто встречаются в электрических и связных системах, технологических линий, а также при структурном резервировании.

Для расчета надежности систем типа “m из n“ при сравнительно небольшом количестве элементов можно воспользоваться методом прямого перебора. Он заключается в определении работоспособности каждого из возможных состояний системы, которые определяются различными сочетаниями работоспособных и неработоспособных состояний элементов.

Некоторые состояния системы “2 из 5“ занесены в табл. 3.1. Для данной системы работоспособность определяется лишь количеством работоспособных элементов. По теореме умножения вероятностей вероятность любого состояния определяется как произведение вероятностей состояний, в которых пребывают элементы. Например, в строке 3 описано состояние системы, в которой отказали элементы 4 и 5, а остальные работоспособны. При этом условие “2 из 5“ выполняется, так что система в целом работоспособна. Вероятность такого состояния

(предполагается, что все элементы равнонадежны). С учетом всех возможных состояний вероятность безотказной работы системы может быть найдена по теореме сложения вероятностей всех работоспособных сочетаний. Для этого суммируются вероятности неработоспособных состояний (где не выполняется условие “ 2 из 5 “)

(3.13)

Тогда вероятность безотказной работы системы

(3.14)

Таблица 3.1

Таблица состояний системы “2 из 5”

	Состояние элементов	Состояние	Вероятность
состояния						системы	состояния системы
	+	+	+	+	+	+
	+	+	+	+	-	+
	+	+	+	-	-	+
	+	+	-	-	-	+
	+	-	-	-	-	-
	-	-	-	-	-	-

 

 

9. Системы типа “m из n”. Комбинаторный метод.

Расчет надежности системы “m из n“ может производиться комбинаторным методом, в основе которого лежит формула биномиального распределения. Биномиальному распределению подчиняется дискретная случайная величина k - число появлений некоторого события в серии из n опытов, если в отдельном опыте вероятность появления события составляет p. При этом вероятность появления события ровно k раз определяется

(3.15)

где - биномиальный коэффициент, называемый “числом сочетаний по k из n“ (т.е. сколькими разными способами можно реализовать ситуацию “k из n“):

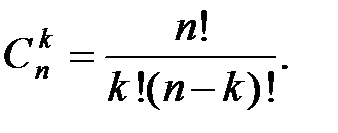(3.16)

Поскольку для отказа системы “m из n“ достаточно, чтобы количество исправных элементов было не меньше m, вероятность отказа может быть найдена по теореме сложения вероятностей для k = 0, 1,... (m-1):

(3.17)

Аналогичным образом можно найти вероятность безотказной работы как сумму (3.15) для k=m, m+1,..., n:

(3.18)

В табл. 3.2 приведены формулы для расчета вероятности безотказной работы систем типа “m из n“ при m<=n<=5. Очевидно, при m=1 система превращается в обычную систему с параллельным соединением элементов, а при m = n - с последовательным соединением.

Таблица 3.2

	Общее число элементов, n
m
	-
	-	-
	-	-	-
	-	-	-	-

 

 

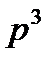
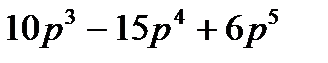
⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: