 |
Типы систем по Стекольникову
|
|
|
|
Все системы по связи элементов, входящих в неё, делятся на:
АССОЦИАТИВНЫЕ СИСТЕМЫ – системы, у которых между элементами отсутствуют структурные отношения. Обозначаются как «А-системы». Примером такой системы может быть совокупность однородных единиц ресурсов, например, лесных. В лесу может быть тысяча деревьев, и они не связаны между собой структурно. Однако они объединены ассоциацией – то есть одинаковым назначением. Способность такой системы зависит от количества оставшихся в строю элементов.
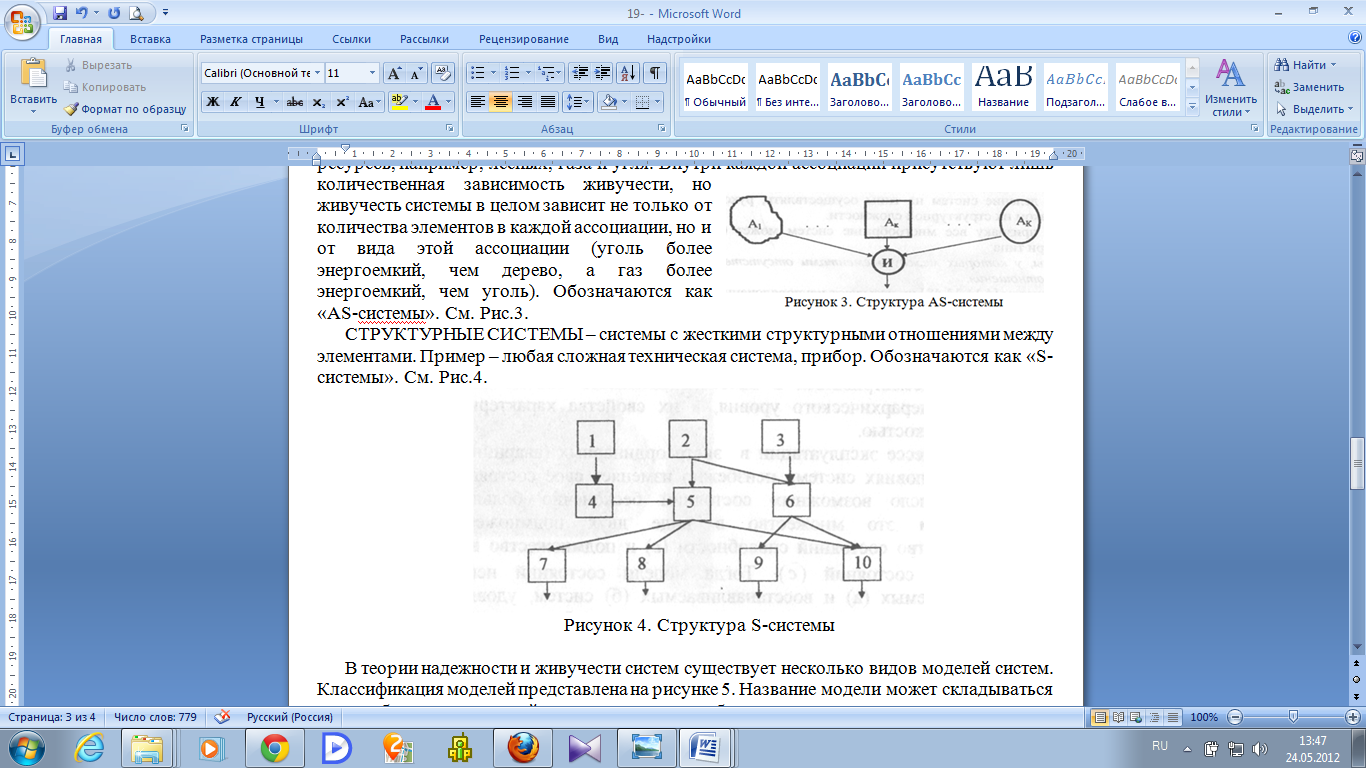
 АССОЦИАТИВНО-СТРУКТУРНЫЕ СИСТЕМЫ – системы со структурными отношениями между ассоциациями. Примером может служить система из разных видов ресурсов, например, лесных, газа и угля. Внутри каждой ассоциации присутствуют лишь количественная зависимость живучести, но живучесть системы в целом зависит не только от количества элементов в каждой ассоциации, но и от вида этой ассоциации (уголь более энергоемкий, чем дерево, а газ более энергоемкий, чем уголь). Обозначаются как «AS-системы». См. Рис.3.
АССОЦИАТИВНО-СТРУКТУРНЫЕ СИСТЕМЫ – системы со структурными отношениями между ассоциациями. Примером может служить система из разных видов ресурсов, например, лесных, газа и угля. Внутри каждой ассоциации присутствуют лишь количественная зависимость живучести, но живучесть системы в целом зависит не только от количества элементов в каждой ассоциации, но и от вида этой ассоциации (уголь более энергоемкий, чем дерево, а газ более энергоемкий, чем уголь). Обозначаются как «AS-системы». См. Рис.3.
СТРУКТУРНЫЕ СИСТЕМЫ – системы с жесткими структурными отношениями между элементами. Пример – любая сложная техническая система, прибор. Обозначаются как «S-системы». См. Рис.4.
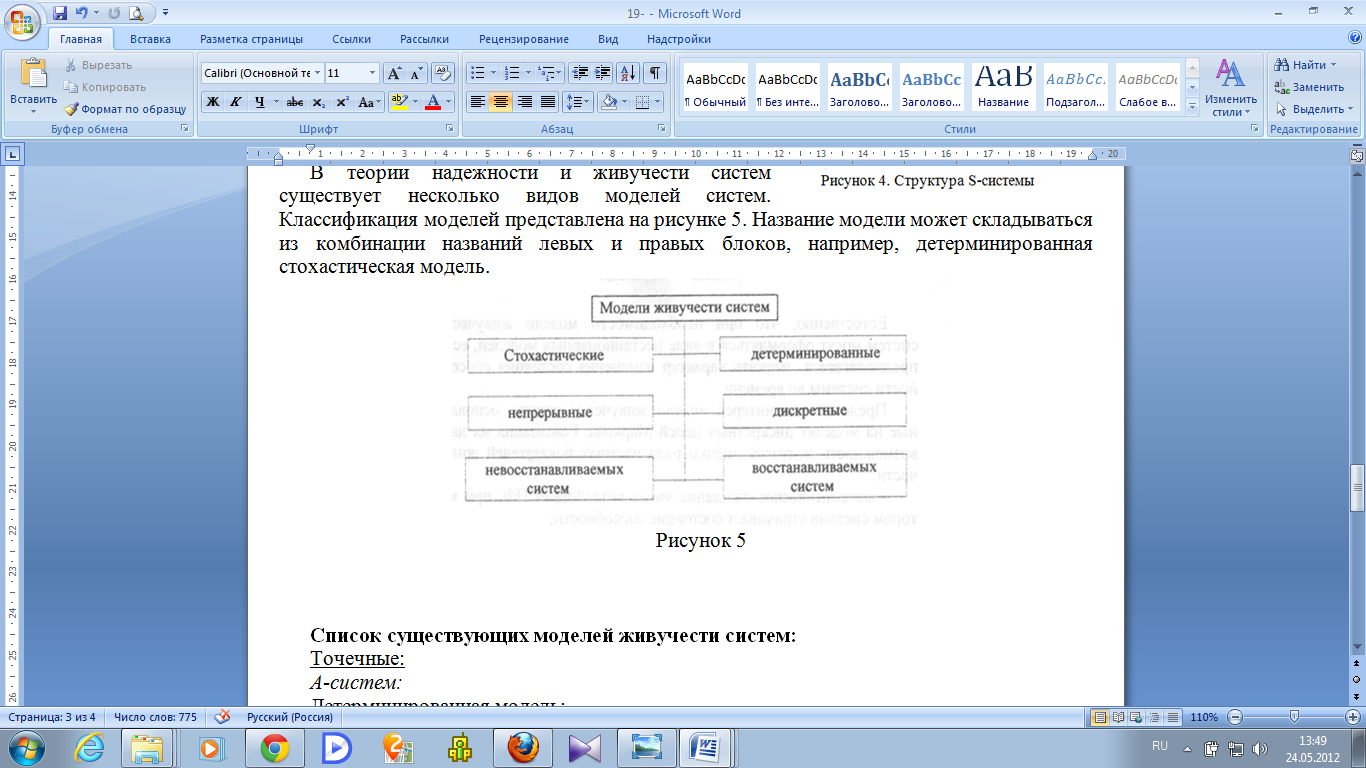 В теории надежности и живучести систем существует несколько видов моделей систем. Классификация моделей представлена на рисунке 5. Название модели может складываться из комбинации названий левых и правых блоков, например, детерминированная стохастическая модель.
В теории надежности и живучести систем существует несколько видов моделей систем. Классификация моделей представлена на рисунке 5. Название модели может складываться из комбинации названий левых и правых блоков, например, детерминированная стохастическая модель.
Список существующих моделей живучести систем:
Точечные:
А-систем:
Детерминированная модель;
Непрерывная стохастическая;
Дискретная стохастическая.
Основанная на приемах комбинаторики;
|
|
|
АS-систем:
Детерминированная;
Универсальная модель;
Основанная на моделях живучести А-систем;
S-систем;
Динамические:
Имитационные модели процессов;
Модели живучести невосстанавливаемых систем в схеме марковского процесса;
22. Модели живучести ассоциативных систем
Существенной особенностью А-систем является ассоциативный характер объединения элементов. Отсутствие структурных отношений между элементами определяет специфику моделирования свойства живучести А-систем. Элементы систем данного типа однородны по назначению. Следовательно, можно утверждать, что в процессе воздействия ПФ свойство соответствия системы своему назначению не претерпевает изменений. Деградация системы идет в направлении свойства достаточности. Данное утверждение лежит в основе "механизма" идентификации состояний способности А-систем. Показателем свойства достаточности систем с однородными элементами является величина ущерба (У). Очевидно, используя величину ущерба, можно формировать Д - признак для идентификации состояний способности системы.
Ясно, что А-система способна решить свойственную задачу, если
У<УД
где Уд - допустимый (по условиям эффективности функционирования) ущерб системы.
В процессе идентификации состояний систем величина Уд играет роль критерия состояний способности и характеризует потерю такого количества материальных средств, при которой остаточный ресурс системы м0 обеспечивает эффективное решение поставленной задачи.
Детерминированная модель живучести А-систем
Непременной особенностью данных моделей является наличие двух конфликтующих систем (Н - хищник, Т - жертва). Если известны возможность Н-системы уничтожать элементы Т-системы с интенсивностью λн, а также способность Т- системы воспроизводить элементы со скоростью λТ, то динамика взаимодействия систем будет характеризоваться изменением показателей эффективности этих систем. Данное изменение предполагалось определять соотношением количеств элементов систем z:
|
|
|

где п,пн - число элементов Т- и Н -систем соответственно.
Данная модель должна рассматриваться как модель устойчивости системы Т, так как в ней комплексируются свойства живучести со способностью системы Т уничтожать элементы системы Н (свойство обороноспособности).
Обосновывая закон поражения элементов системы и задаваясь начальными условиями, возможно получить общее решение, характеризующее динамику деградации Т-системы с учетом способности ее к восстановлению или доукомлектованию элементов. 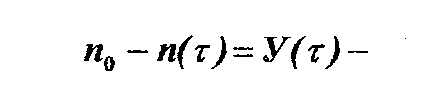 - величина текущего ущерба.
- величина текущего ущерба.
Непрерывная стохастическая модель живучести А-систем
Рассмотрим А-систему, живучесть которой обеспечивается не только наличием избыточных элементов, но и проведением мер по восстановлению утративших работоспособность элементов. В такой постановке представляет интерес величина остаточного ущерба У0 которая также случайна.
Очевидно.что 
где УП - предотвращенный ущерб системы в результате восстановительных мер.
С учетом показатель живучести А-системы может быть рассчитан как вероятность события, состоящего в том, что величина остаточного ущерба не превышает допустимого значения (Уд):
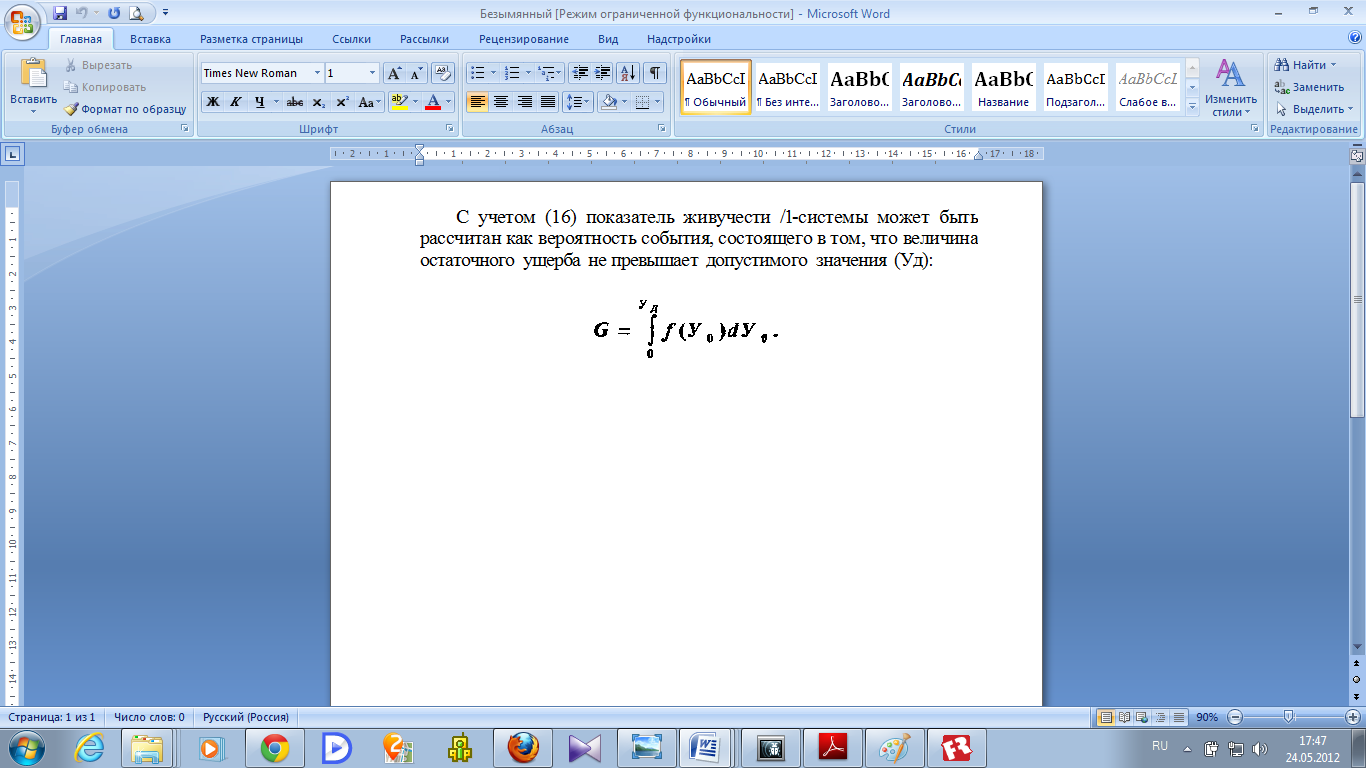 Практическое применение рассмотренной модели живучести А-систем предполагает предварительное накопление статистического материала по величинам текущего и предотвращенного ущерба. Реально данный материал может быть получен с помощью имитационных моделей.
Практическое применение рассмотренной модели живучести А-систем предполагает предварительное накопление статистического материала по величинам текущего и предотвращенного ущерба. Реально данный материал может быть получен с помощью имитационных моделей.
Дискретная стохастическая модель живучести А - систем
В основу дискретной стохастической модели живучести положим гипотезу о биномиальном распределении случайной величины числа уничтоженных элементов системы (х) при воздействии ПФ по схеме независимых испытаний. Пусть система состоит из n однородных по назначению элементов. Состояние способности системы идентифицируется с величиной необходимого ресурса т, т.е. потребным числом элементов в работоспособном состоянии. имеет смысл рассматривать случай, когда т<п.
Ясно, что п - т = Уд - допустимый ущерб системы. Тогда модельное представление показателя живучести в рассматриваемой постановке может быть описано выражением
|
|
|
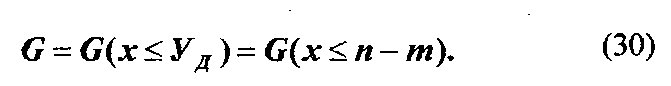 Вид функциональной зависимости G(x,n,m) может быть получен с помощью известного аналитического аппарата биномиального распределения дискретных случайных величин. Показатель живучести А-систем при ω-кратном воздействии ПФ:
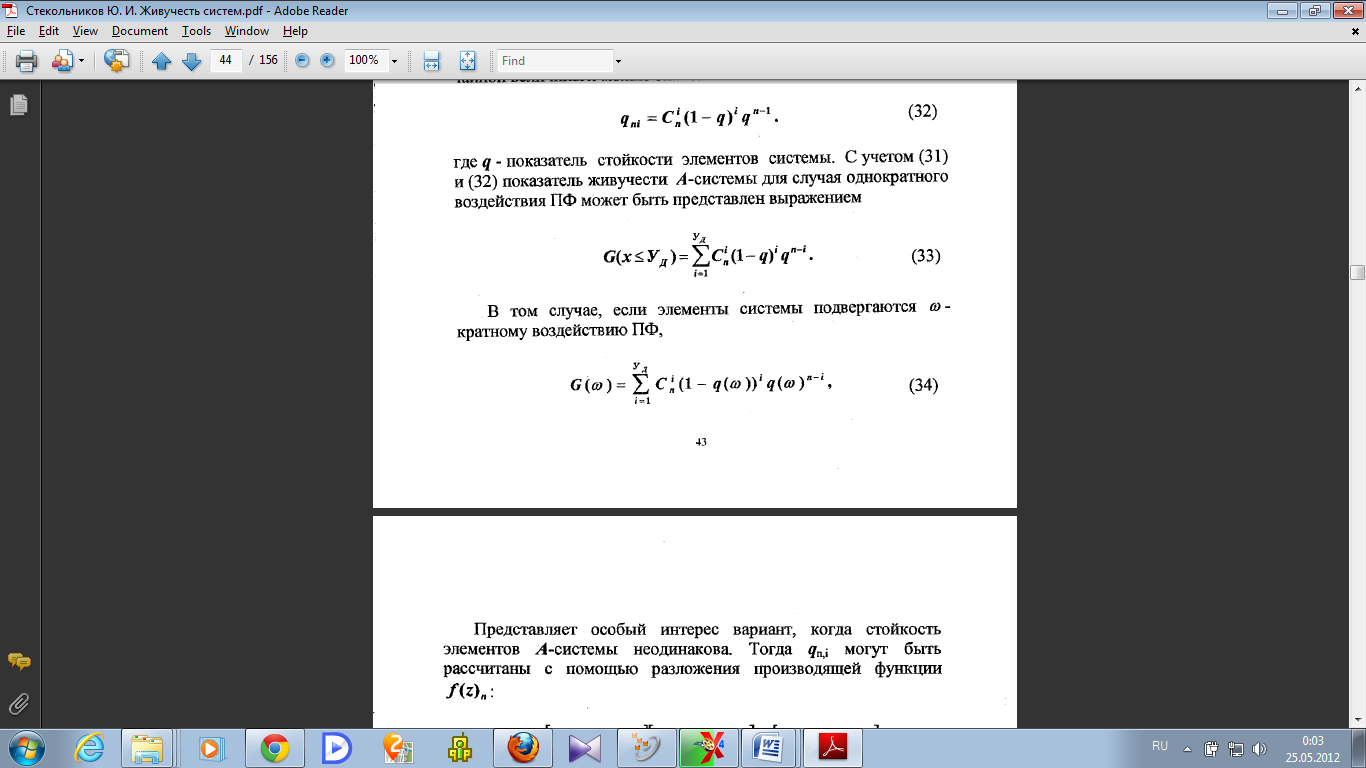
Вид функциональной зависимости G(x,n,m) может быть получен с помощью известного аналитического аппарата биномиального распределения дискретных случайных величин. Показатель живучести А-систем при ω-кратном воздействии ПФ:
, где q- показатель стойкости элементов системы
23. Модели живучести ассоциативно-структурных систем
Существенной особенностью АS-систем, определяющей способ моделирования и вид модели живучести, является ассоциативный характер объединения элементов и наличие признаков структурных отношений между ассоциациями.
Спецификой, отличительной чертой АS-систем по отношению к А-системам следует отметить более сложный "механизм" идентификации состояний способности. Суть заключается в том, что структурные отношения между ассоциациями порождены потребностью обеспечения функционирования системы в определенном "технологическом цикле". Система будет способна решать поставленную задачу, если ее остаточный ресурс будет содержать необходимое количество (Д-признак) элементов в каждой ассоциации (С-признак).
Детерминированная модель
 Если АS-система составлена из n элементов, распределенных по К ассоциациям (nK), то "механизм" идентификации состояний способности должен предполагать соблюдение условий:
Если АS-система составлена из n элементов, распределенных по К ассоциациям (nK), то "механизм" идентификации состояний способности должен предполагать соблюдение условий:
,где tK - число элементов k - й ассоциации, сохранивших работоспособность после воздействия ПФ; тК - необходимый ресурс k-й ассоциации.
Условие (39) определяет реализацию признака достаточности (Д-признак), а (40) является обязательным для подтверждения признака соответствия (С-признак).

 - вероятность события, состоящего в том, что после воздействия ПФ остаточный ресурс системы содержит элементы всех К ассоциаций, а их количество не менее необходимого (mk)
- вероятность события, состоящего в том, что после воздействия ПФ остаточный ресурс системы содержит элементы всех К ассоциаций, а их количество не менее необходимого (mk)
- логическая модель живучести АS-систем.
Универсальная модель
В основе данного подхода лежит обобщенная модель живучести AS-систем. Очевидно, разработка искомой модели сводится к установлению функциональной зависимости (42) при к = 1,2,...K. Решение этого вопроса свяжем с существующей возможностью подсчета количества состояний способности системы L с учетом принятого закона поражения ее элементов.
|
|
|
Сделаем допущение о том, что зона действия ПФ безгранична и воздействию подвергаются все элементы системы. Показатели стойкости элементов сугубо индивидуальны.
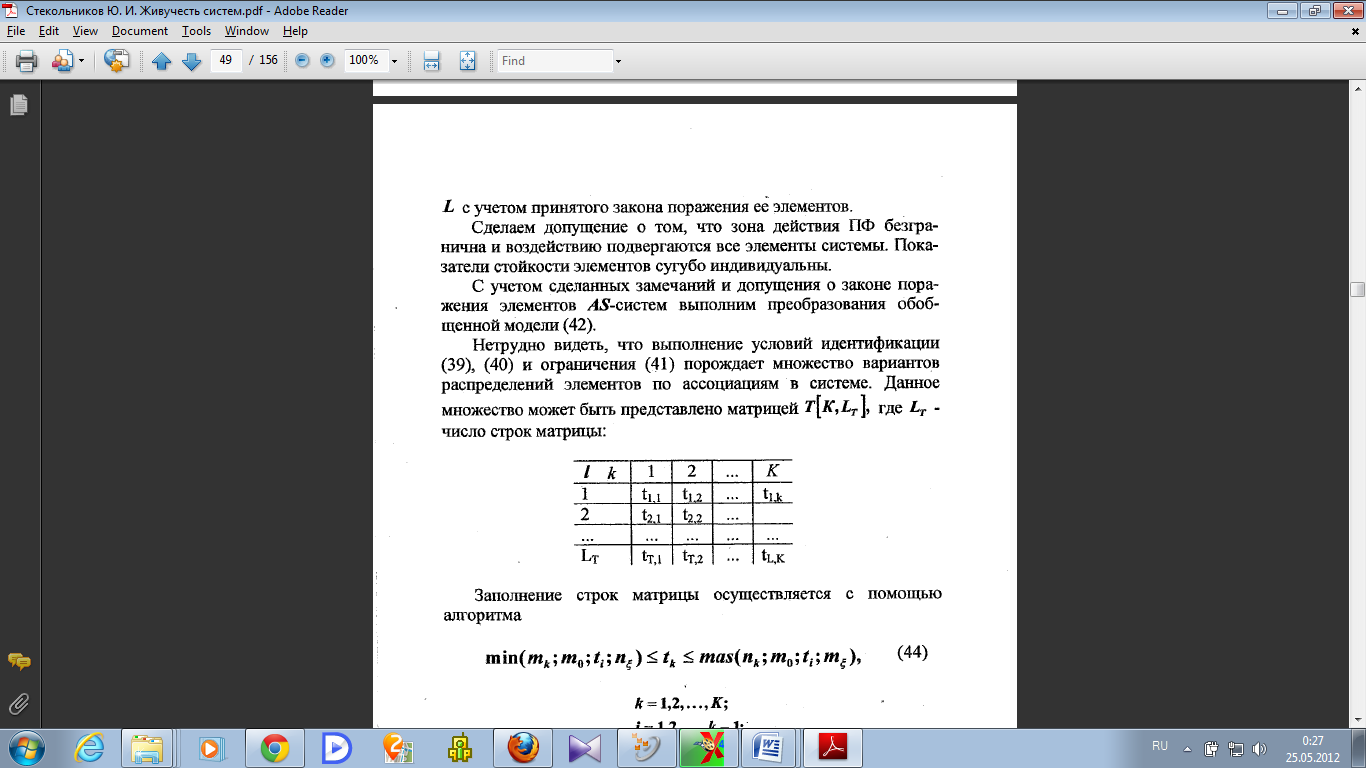 С учетом сделанных замечаний и допущения о законе поражения элементов AS-системы выполним преобразования обобщенной модели (42).
С учетом сделанных замечаний и допущения о законе поражения элементов AS-системы выполним преобразования обобщенной модели (42).
Выполнение условий идентификации, и ограничения порождает множество вариантов распределений элементов по ассоциациям в системе. Данное множество может быть представлено матрицей Т[К, LT], где LT -число строк матрицы:
 Если матрица Т рассчитана, то возможна оценка числа состояний способности AS-системы. Так как элементы в каждой ассоциации однородны по назначению, то число возможных вариантов содержания в каждой k-й ассоциации ровно t1,k элементов из nk возможных равно
Если матрица Т рассчитана, то возможна оценка числа состояний способности AS-системы. Так как элементы в каждой ассоциации однородны по назначению, то число возможных вариантов содержания в каждой k-й ассоциации ровно t1,k элементов из nk возможных равно
Число любых исходов L0 в данных условиях равно Спm0. Тогда при достаточно большом числе элементов рассматриваемая модель живучести AS-системы может быть представлена выражением
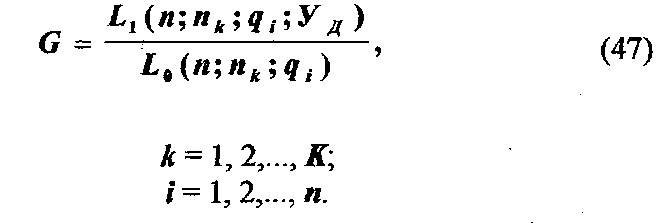
Показатель живучести AS-системы в виде модели (47) критичен к числу элементов системы (n), к особенностям "технологии" функционирования (nk), к показателю стойкости элементов (q) и к требованию эффективности решения системой поставленной (свойственной) задачи (Уд).
Модель живучести AS-системы, основанная на моделях живучести А- систем
Любую AS-систему можно представить как совокупность А-систем, к каждой из которых предъявляются индивидуальные требования, т.е. остаточный ресурс k-й ассоциации (tk) должен быть не менее необходимого (тк) для сохранения системой состояния способности.
Если для заданных условий боевой или аварийной обстановки определены показатели живучести (Gk) всех К ассоциаций AS-системы, то показатель живучести системы с учетом условия идентификации может быть рассчитан с помощью
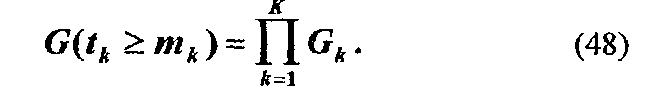
Модели, на основе которых производится оценка (Gk) выбираются среди моделей живучести A-систем в зависимости от целей исследования и требования к точности решения задачи.
Различные варианты модельного представления свойства живучести AS-систем обладают различными возможностями по исследованию данного свойства и точности оценки его показателей. Правильный выбор модели при решении тех или иных задач во многом определяет содержание и трудоемкость вычислительной процедуры.
|
|
|


