Модели живучести S-систем. МСС,ФСС, КПУФ. Имитационные модели процессов.

Структурные (.S-системы) наиболее распространенный тип систем. Отличительным признаком S-систем является четко выраженная структура. Элементы различного назначения здесь находятся в жестких структурных отношениях. Эти отношения, а также характеристики элементов, подчинены не только свойственным системе особенностям функционирования, но и требованию эффективности. Объединение ряда однородных по назначению элементов в ассоциации практически невозможно, так как отношения в структуре, как правило, организуются не между группами (ассоциациями), а между отдельными элемента­ми. Эта отличительная особенность S-систем определяет подход к моделированию свойства живучести. В основе предполагаемого подхода лежит уникальная возможность априори перечислять все состояния способности системы.

Данные перечисления могут оформляться в виде:.

- матрицы состояний способности (МСС) Б [x_il] i=1,2,...,n₁ - число элементов, обеспечивающих l - е состояние способности. Здесь x_il - логическая переменная, характеризующая причастность i-го элемента к обеспечению l - го состояния способности;

- логической функции состояний способности (ФСС) У(x_n), представленной в дизъюнктивной нормальной (ДНФ) или в совершенной дизъюнктивной нормальной форме (С ДНФ).

"Механизм" идентификации состояний способности при построении МСС и ФСС предполагает учет обоих признаков идентификации - соответствия и достаточности.

С-признак удовлетворяется подбором подмножеств элемен­тов [x_il] в строках МСС и в конъюнкциях ФСС с учетом особен­ностей функционирования S-системы в заданном техноло­гическом цикле. Д -признак удовлетворяется тем, что данный технологический цикл обеспечивает необходимую произво­дительность или заданное время функционирования системы. Методы формирования подмножеств [х_й] или кратчайших путей успешного функционирования (КПУФ) достаточно хорошо разработаны и многообразны.

В том случае, если МСС или ФСС разработаны, процесс мо­делирования свойства живучести сводится к оценке шанса, что после воздействия ПФ остаточный ресурс т₀ позволит сформиро­вать хотя бы один КПУФ или хотя бы одно состояние способнос­ти системы, т.е.

 

Данный шанс может вычисляться с помощью стохасти­ческих моделей живучести.S-систем или логических моделей

 

Имитационные модели процессов

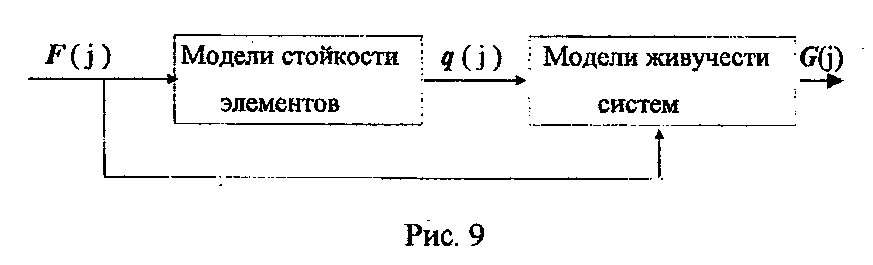Подход к исследованию динамики изменения свойства живу­чести на имитационных моделях основан на определенной после­довательности использования моделей стойкости элементов и моделей живучести систем в одном блоке и в единых условиях внешних воздействий (рис.9).

 

Вход в модель F (j) формируется исходя из потребности исследования свойства живучести системы в тех или иных усло­виях. На выходе при этом возможно проследить характер изме­нения показателя живучести при изменении по определенному закону j-х условий.

Возможности данного подхода моделирования процессов из­менения свойства живучести систем достаточно широки:

- при j=τ (текущее время) с помощью соответствующих мо­делей возможна оценка стойкости элементов q(τ) и зависимости показателя живучести от времени G(ω);

- при j =ω, где ω =1,2,... - число воздействий ПФ на эле­менты системы возможен расчет q(ω), а затем и частного показателя живучести системы G(ω)- УЗН;

-при j = ω₁, где ω₁=1,2,... - число элементов, изъятых из структуры системы возможен расчет G(ω₁) - УЗНС.

 

 

25. Модели живучести невосстанавливаемой системы в схеме марковского процесса.

Описывает последовательное состояние системы, каждое последующее состояние не зависит от предыдущих.

В принятых условиях правомерно применение аппарата цепей Маркова для моделирования процесса сохранения системой состояния способности в дискретном времени или при многократном воздействии ПФ.

Полный граф состояний системы с одним поглощающим сос­тоянием показан на рис. 10.

На рисунке обозначены: С₀ - исходное состояние, от кото­рого начинается движение системы в пространстве состо­яний; C₁ ,..., С_l,..., C_L - состояния способности системы, модели­руемые ФСС; С- обобщенное состояние неспособности системы, наделенное свойством поглощения.

Так как исследуется невосстанавливаемая система, то пе­реходы С_/=, -» C_t невозможны и матрица вероятностей переходов 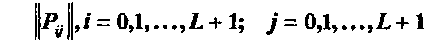является диагональной

Конъюнкции ФСС в СНДФ имеют одинаковый ранг R = п -число элементов в системе и составлены из логических пере­менных x_i, принимающих два значения: Х_i,l - элемент структуры

Обеспечивает l-e состояние способности; ẋ _i,l - не обеспечивает.

Поразрядное сравнение конъюнкций ФСС, соответствую­щих l -му и l +1-му состояниям способности, дает возможность получить логическую функцию перехода (ЛФП) P_l,l+1.

Правила поразрядного сравнения конъюнкций формирующие ЛФП, приведены в табл.2.

Предполагается, что ЛФП, полученная с помощью этих пра­вил, может быть легко преобразована в вероятностную функцию переходов (ВФП) путем замены логических переменных x_i на со­ответствующие показатели стойкости q_i.

Вычисление ВФП дает возможность получить искомую вероятность перехода P_l,l+1

Рассмотренная динамическая модель живучести систем, основанная на модели марковского процесса, является удобным инструментом для исследования динамики изменения ве­роятностей пребывания системы в каждом из L состояний спо­собности.

Практическое значение полученных знаний состоит в воз­можности прогнозирования состояния системы в заданных условиях и планирования запасов различного рода ресурсов, необходимых для восстановления конкретного (наиболее веро­ятного) состояния способности.

 

 

26. Модели стойкости элементов. Параметрическая и геометрическая модели.

Элементы систем могут находиться в двух состояниях: работоспособном (r) и неработоспособном (ṝ). Переход состояний может быть как в одном ( r→ ṝ), так и в обратном ( r← ṝ) направлениях. На рис.11 представлены графы состояний невосстанавливаемых (а) и восстанавливаемых (б) элементов.

Воздействие ПФ на элементы восстанавливаемых систем сопровождается переходом их состояний в обоих направлениях.

Очевидно, что при разработке модели стойкости элементов должны быть учтены:

- характеристики ПФ и особенности их воздействия на элементы системы;

- свойство элементов выдерживать определенные нагрузки ПФ;

-возможности системы и приспособленность элементов к восстановлению работоспособности после воздействия ПФ. В связи с этим моделирование стойкости элементов многовариантно (рис.12).

Возможные типы моделей определяются свойствами эле­ментов (восстанавливаемые, невосстанавливаемые), способом оценки их работоспособности (параметрические, геометричес­кие), характером формирования разрушающего воздействия ПФ (стационарные, нестационарные) и особенностями условий, при которых требуется оценка стойкости элементов (непрерывные, дискретные).

Параметрические модели

Разрушающее воздействие ПФ на элементы системы характе­ризуется некоторым параметром, который назовем внешней наг­рузкой N_B.

Данной внешней нагрузке "противостоят":

- защита элемента от воздействия ПФ определённого вида (амортизация, бронирование, тепловая защита и т.п.). Будем задавать защитные свойства элементов некоторым коэффициентом защищенности К₃;

- потенциальная "прочность" элемента, которая может быть характеризована величиной нагрузки N_p(расчетная нагрузка), на которую был рас­считан элемент при проектировании.

Для удобства моделирования свойства стойкости элементов введем понятие действующей нагрузки N_Д- т.е. нагрузки, ко­торая непосредственно воздействует на элемент, преодолевая его защиту.

Ясно, что

Соотношение действующей и рас­четной нагрузок будет однозначно определять состояние эле­мента. Элемент утрачивает работоспособность в случае превы­шения действующей нагрузки над расчетной.

При разработке моделей полезно использовать понятие резерва нагруженности элемента (R), величина которого характеризует превышение расчетной нагрузки над действующей:

При этом модель преобразуется в модель стойкости элементов

Существуют ПФ, действующая нагрузка которых зависит от продолжительности их воздействия, т.е. является функцией времени N_Д(τ) (тепловой поток, радиоактивное заражение и т.п.). Процесс поражения элементов здесь нестационарен. Так, внешняя нагрузка в виде теплового потока вызывает нарастание температуры конструкций элементов, которая с течением време­ни может превысить расчетное значение.

С учетом особенностей данных ПФ стационарные модели стойкости преобразуются в нестационарные:

Практическая ценность этих моделей заключается в воз­можности оценивания динамики изменения показателя стойкости элементов во времени.

Геометрические модели

Разработка такого класса моделей стойкости элементов основывается на геометрическом под­ходе, когда учитываемые параметры ПФ приводятся в соответствие с расстоянием р от источника ПФ. Если это соот­ветствие установлено, то всегда можно найти такое расстояние Р- Р_б, находясь на котором от источника ПФ элемент системы не утратит работоспособности с высокой вероятностью.

В основе методик обоснования значений р_б лежит параметрический подход к оценке стойкости элементов. Очевидно, что величина р_б является решением уравнения при условии равенства нулю резерва нагруженности: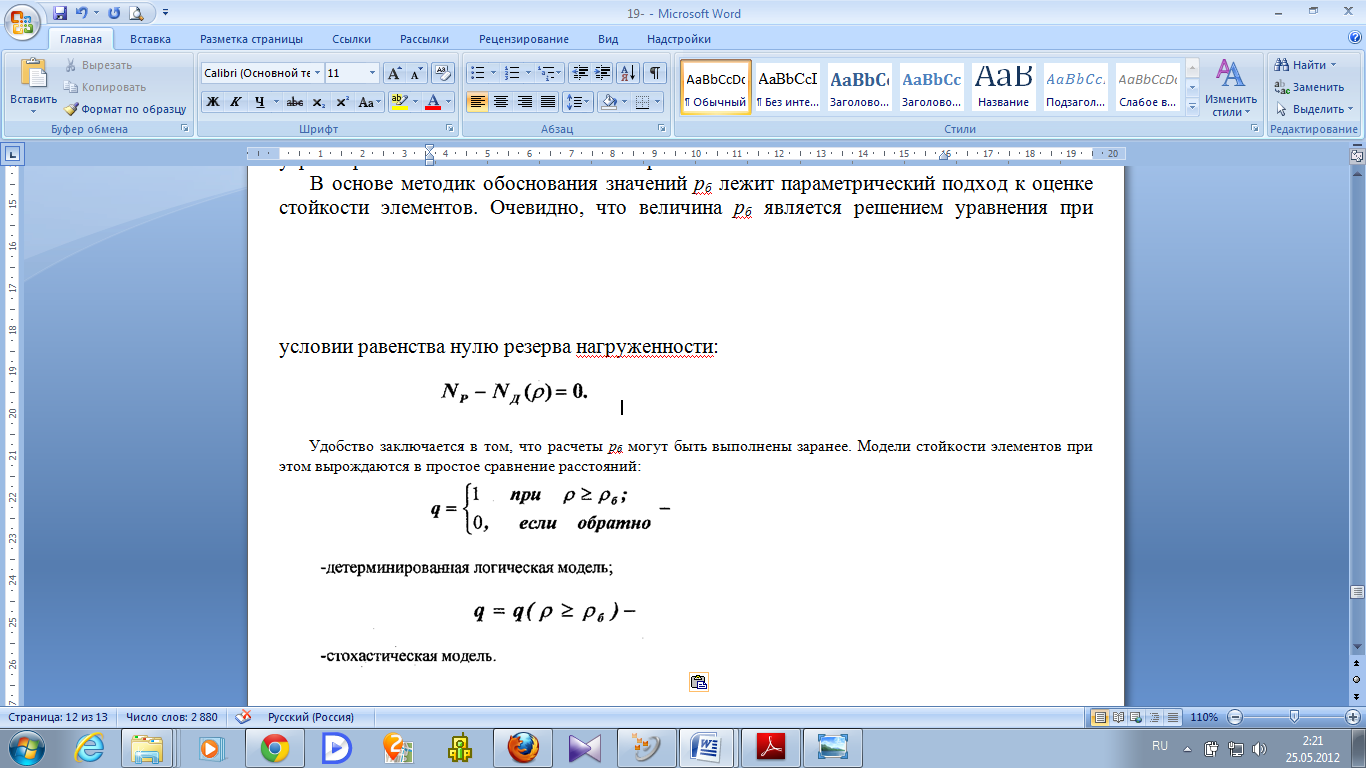

Удобство заключается в том, что расчеты р_б могут быть выполнены раранее. Модели стойкости элементов при этом вы­рождаются в простое сравнение расстояний:

 

 

⇐ Предыдущая123456

Поделиться:

Воспользуйтесь поиском по сайту: