 |
Величин, используемые в теории надежности
|
|
|
|
Широкое применение экспоненциального закона объясняется тем, что для большинства задач теории надежности он наиболее прост и удобен для использования.
Почти все формулы в теории надежности в случае экспоненциального закона значительно упрощаются.
Однако применение экспоненциального закона зависит в основном от характера отказов элементов. Внезапные отказы, носящие случайный характер, обычно довольно хорошо описываются экспоненциальным законом. Другие типы отказов, например отказы, возникающие в результате износа, в результате необратимых физико-химических изменений параметров элемента, не подчиняются экспоненциальному закону. Эти отказы, носящие название постепенных, описываются другими законами теории надежности, в частности, нормальным законом распределения.
Поэтому мы кратко рассмотрим основные законы распределения, которые применяются в теории надежности.
Нормальный закон распределения случайной величины. Для случайной величины времени отказа изделия T функция распределения (то есть вероятность того, что за время t возникает отказ) определяется формулой:

Плотность отказов выражается следующей формулой:
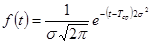 ,
,
где s и Тср – параметры закона распределения:
s – среднеквадратичное отклонение T относительно Tср , а
Tср – это среднее значение Т.
Биноминальный закон распределения числа n появления события А
в m независимых испытаниях. Если вероятность появления события А в одном испытании равно p, вероятность не появления равна g=1 – p, число независимых испытаний m, то вероятность появления n событий равна
 ,
,
где  – число сочетаний из n по m.
– число сочетаний из n по m.
 .
.
Закон Пуассона. По этому закону вероятность числа n – случайных событий за время t определяется по формуле:
|
|
|
 ,
,
где l – (среднее число событий в единицу времени) – это интенсивность появления случайного события,
lt – это среднее число событий за время t.
Отличительными чертами сложных систем, к которым относят системы обработки данных (ВС), являются:
– многоканальность, то есть наличие нескольких каналов, каждый из которых выполняет определенную функцию, частную по отношению к общей задаче системы
– многосвязанность, т.е. большое количество функциональных связей между элементами системы,
– наличие вспомогательных и дублирующих устройств.
Благодаря перечисленным особенностям сложная система может находиться в нескольких рабочих состояниях, так как выход из строя некоторых элементов не вызывает полного отказа системы, но ухудшает в той или иной степени качество функционирования.
Следовательно, отказ элемента переводит систему из полной работоспособности в состояние частичной работоспособности.
ВС можно характеризовать функциональной и эффективностью надёжностью.
Функциональная надёжность Рф – это вероятность того, что данная система будет удовлетворительно выполнять свои функции в течении заданного времени.
Эффективная надёжность Рэ – среднее значение (мат. ожидание) величины, характеризующей относительный объем и полезность выполняемых системой функции в течение заданного времени по сравнению с ее предельными возможностями.
Введение критерия эффективной надежности объясняется тем, что одними показателями надежности, взятыми отдельно, не удается оценить функционирование сложной системы.
Сложная система кроме надежности каждого блока и всей системы характеризуется еще и относительной важностью потери системой тех или иных качеств. Поэтому под эффективной надёжностью Рэ понимается некоторая количественная мера, оценивающая качество выполнения системой своих функций.
|
|
|
Пусть система находится в каком-либо состоянии j. Эффективную надёжность этой системы в данном состоянии называют частной или условной эффективностью. Это может быть вероятность того, что система, находясь в состоянии j, способна решить задачу, выбранную случайным образом (независимо от состояния j) в соответствии с некоторым вероятностным законом из определенного множества задач.
Частная эффективность системы характеризуется вероятностью получения этой эффективностью. В общем случае эффективная надёжность системы со счетным множеством дискретных состояний определяется как математическое ожидание выходного эффекта
 ,
,
где Pj(t) – вероятность того, что система окажется в состоянии j,
Ej – эффективная надёжность системы в j–м состоянии.
Иногда Ej называют коэффициент сохранения эффективности Кэф. Он определяется весовым коэффициентом, характеризующим важность выполнения системой функций в j–м состоянии сравнительно с полным объемом функций, возложенных на систему.
Коэффициент эффективности Ej показывает, насколько снижается работоспособность системы при отказе данного элемента. Он может принимать значение от 0 до 1.
Для элементов, отказ которых не влияет на выполнение системой основных функций, устанавливается коэффициент эффективности Ej = 0.
Элементы, отказ которых приводит к полному отказу системы, имеют коэффициент эффективности Ej = 1.
Рассмотрение количественных показателей надежности, а так же анализ характеристик надежности сложных систем позволяет сделать следующие выводы:
1 Надёжность сложной системы имеет характер системы показателей. Чем большее число показателей надежности систем определяется при анализе ее надежности, тем более подробным становится этот анализ. Но это не означает, что всякий раз либо при анализе надежности, либо при задании требований к надежности, надо использовать весь перечень возможных показателей надежности. Перечень используемых показателей надежности должен быть не просто возможно более полным, но и целесообразным, то есть отвечающим задаче объективной характеристики требуемых свойств системы;
2 В системе показателей надежности целесообразно выделять главные показатели и вспомогательные. В отдельных случаях, например, определение ремонтопригодности, живучести, достоверности или сохраняемости может оказаться неактуальным и даже ненужным. В других случаях показатели достоверности или живучести могут стать главными показателями надежности системы.
|
|
|
3 Количественные значения показателей надежности следует задавать с учетом двух противоположных требований: с одной стороны, показатель надежности должен быть не ниже некоторого уровня, который обеспечивает требуемую эффективность, с другой стороны, он не должен превышать уровня, который может быть обеспечен возможностями производства.
Задача проектирования состоит в том, чтобы выбором принципиальной схемы объекта, алгоритма работы и средств обеспечения надежности выполнить эти два противоречивые требования. Для этого необходим всесторонний анализ возможных вариантов решения поставленной задачи с привлечение расчётов и моделирования.
4 Дальнейшее совершенствование показателей надежности продолжает оставаться актуальной задачей. Важнейшими направлениями их совершенствования является разработка следующих показателей:
– показателей надежности, основанных на признании практической безотказности особо ответственных изделий на заданном интервале использования;
– показателей надежности, учитывающих индивидуальную надёжность конкретных изделий;
– показателей надежности, учитывающих влияние надежности на эффективность, влияние программного обеспечения, человеческого фактора, а также живучести и достоверности.
Вопросы для самоконтроля
1. Что такое надёжность ВС (определение)?
2. Каковы понятия безотказности, ремонтопригодности, долговечности и сохраняемости?
3. Каковы функции надежности?
4. Что такое надёжность элемента, работающего до первого отказа?
5. Сущность экспоненциального закона надежности?
6. Приведите формулы расчёта эмпирических функций:
- вероятности отказа элемента до момента времени t;
- плотности распределения отказов;
- вероятности безотказной работы;
- интенсивность отказов.
7. Какова сущность участков графика функции интенсивности отказов?
8. Как используется экспоненциальный закон для расчёта значений функций надежности?
9. Каково среднее время жизни элемента?
|
|
|


