 |
Резервирование как метод повышения надежности
|
|
|
|
Резервированием называется способ повышения надежности путем включения резервных блоков, способных в случае отказа основного блока выполнять его функции. Этот метод дает возможность получения заданных уровней надежности, и нашел широкое применение в практике.
В общем случае надёжность не избыточной (не резервируемой) системы определяется как произведение надежностей входящих в нее элементов:

Это уравнение показывает, что выход из строя любого элемента приводит к отказу всего устройства. Создание сложных электронных устройств связано с применением широкого комплекса различных элементов, различающихся по своим свойствам и характеристикам.
Наряду с высоко надежными элементами в данное устройство могут входить и малонадежные, причем надёжность не резервируемого устройства не может превышать надёжность самого ненадежного элемента.
Поэтому при синтезе высоконадежных систем необходимо применять резервирование. Если имеется система из S параллельных элементов (рисунок 2.3), а вероятность неисправной работы i-го элемента Qi, то вероятность выхода из строя системы
 ,
,
а вероятность исправной работы
 .
.
 |
Рисунок 2.3 - Параллельное включение элементов
Следовательно, чем больше элементов S, тем больше надёжность Р, то есть с увеличением числа резервных элементов надёжность системы повышается.
Разнообразные методы резервирования и способы включения резерва могут быть сведены к трем методам резервирования:
- общему;
- раздельному;
- комбинированному (смешанному).
Общим называется такое резервирование, при котором параллельно включаются идентичные системы, раздельным называют резервирование систем путем применения отдельным резервных устройств, а при комбинированном – в одной и том же системе применяют общее и раздельное резервирование.
|
|
|
На рисунке 2.4 представлена система с общим резервированием.
 |
Рисунок 2.4 - Общее резервирование
На рисунке каждая система состоит из w элементов, и параллельно подключено S систем.
При общем резервировании вероятность отказа i-й дублирующей цепочки выражается следующей формулой
 , где
, где
Рij – вероятность исправной работы j-го элемента i-й цепочки.
При общем резервировании отказ системы возникнет в случае отказа в основной и каждой резервной цепи. Отсюда: 
Вероятность исправной работы определяется по формуле:  (32)
(32)
При одинаковых элементах (равно надежных)
 (33),
(33),
где р – надёжность каждого элемента.
На рисунке 2.5 представлена система с раздельным резервированием.
 |
Рисунок 2.5 - Раздельное резервирование
Если при раздельном резервировании система состоит из w элементов, каждый из которых имеет надёжность Pj и представляет собой S параллельно соединенных элементов, то надёжность системы выражается следующей формулой:

Вероятность отказа условного элемента:
 ,
,
где Qij – это вероятность выхода из строя i-го элемента j-й группы.
Тогда формула надежности системы с раздельным резервированием принимает вид:

При равно надежных элементах эта формула примет вид:
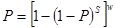
Главным способом включения резервной аппаратуры при отказах основной являются следующие:
- постоянное резервирование, при котором резервные единицы соединены с основными в течении всего времени работы и находятся в одинаковом с ними рабочем состоянии;
- резервирование замещением, при котором резервные единица замещают основные только после отказа.
При этом резервные единицы могут находиться в 3-х режимах работы:
1 Нагруженном (в горячем резерве), при котором резервные единицы находятся в тех же условиях, что и основные.
|
|
|
2 Не нагруженном (в холодном резерве), при котором резервная единица не включена. Считается, что элементы, находящиеся в холодном резерве не отказывают.
3 В облегченном (теплом резерве), при котором резервная единица включена, но без нагрузки, то есть надёжность в резервном состоянии выше, чем в рабочем.
Оптимизация надежности ВС
На практике при проектировании сложных систем возникает задача создания такой системы, которая обеспечивала бы максимальную или заданную эффективную надёжность. Показатель качества функционирования сложной системы улучшают различными путями, в том числе изменением структуры и принципа её функционирования, а также за счет повышения надёжности элементов системы. В связи с этим возникает задача оптимального резервирования системы.
Рассмотрим её в следующей постановке. Имеется сложная многофункциональная система, состоящая из конечного множества элементов N, соединенных определенным образом. Каждый элемент находится либо в состоянии отказа (обозначим его условно xi=0), либо в состоянии работоспособности (обозначим его через xi=1). В произвольный момент времени система оказывается в одном из 2N различных состояний х=[x1, x2,…, xN].
Обозначим через P[y(i),x], частную (условную) эффективность системы (либо качество решения задачи), которая зависит от x. В свою очередь, распределение x зависит от вида функции yi – распределения резерва по элементам.
В качестве критерия оценки надежности сложной системы выбирают эффективность в следующем виде:
 (2.1),
(2.1),
где p(x) – вероятность того, что система находится в состоянии х.
Суммирование производится по всем x, пробегающим 2N возможных значений.
Рассмотрим постановку задачи в двух следующих формулировках:
А) Найти такой закон распределения ограниченных средств, при котором значение средней эффективности системы (2.1) принимало максимальное значение при условии, что
 ,
,
где y0 – заданная избыточность системы.
Таким образом
 (2.2)
(2.2)

С) Найти такой закон распределения минимальных средств, при котором значение средней эффективности системы (2.1) достигло бы заданной эффективности:
|
|
|
 |
 (2.3)
(2.3)
Основными методами решения задач оптимального резервирования являются:
1) Метод прямого перебора, являющийся совершенно точным, однако при большом количестве элементов он становится практически не реализуемым.
2) Метод неопределенных множителей Лагранжа, который позволяет получить нецелочисленные значения, что приводит к необходимости на последнем этапе решения прибегать к непосредственному перебору.
3) Градиентный метод применяется как для ручных так и для машинных вычислений. Основанным его недостатком является то, что он дает точное решение задачи оптимального резервирования только в том случае, когда
 ,
,
т. е. при остановке процесса полученная избыточность в точности равна заданной. Если такого совпадения нет, то полученное решение может считаться лишь приближенно оптимальным.
Рассмотрим применение градиентного метода для сложной системы:
1 Подсчитывают среднюю эффективность системы без резерва P0эi.
2 Вычисляют среднюю эффективность системы при резервировании i-ого
элемента (i=1,2, N):
P1эi.
3 Находят величину прироста эффективности системы при резервировании i-
того элемента:
P1эi- P0эi.
4 Определяют коэффициенты
 ,
,
где Gi –вес (стоимость, объём и т.д.) i-ого элемента.
5 Выбирают наибольший из коэффициентов 
 (5)
(5)
6 К соответствующему элементу добавляют один резервный.
Полученное состояние принимают за исходное, и подобный процесс повторяется до тех пор, пока система не достигнет ограничений (2.2) или (2.3).
|
|
|


