 |
Преобразование стационарного случайного сигнала линейной
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 4
Исследование влияния случайных помех на точность
Линейной системы автоматического управления
Цель работы: Исследование влияния случайных помех на точность линейной системы автоматического управления.
Теоретические сведения
Случайные функции. Основные понятия и определения.
На практике большинство систем автоматического управления (САУ) работает в условиях постоянно действующих случайных воздействий. Различают полезные и вредные воздействия. Полезным, например, является такое воздействие как входной сигнал задания. К вредным случайным воздействиям относят различные внешние и внутренние помехи, изменения нагрузки, напряжения питания сети и т.п. Полезные воздействия система должна обрабатывать по заданному закону управления как можно точнее. Система управления строится таким образом, чтобы вредные случайные воздействия приводили к минимальной ошибке при преобразованиях полезных сигналов.
Для анализа и синтеза систем, подвергающихся воздействию случайных сигналов, необходимо использовать математический аппарат теории случайных функций.
Случайная функция X(t) (случайный процесс) это такая функция времени, значение которой в каждый конкретный момент времени t невозможно предсказать заранее, т.е. является случайной величиной. При наблюдении за случайной функцией во время проведения эксперимента можно получить множество ее значений в различные моменты времени. Полученная серия экспериментальных данных представляет собой реализацию случайной функции. Бесконечное множество возможных реализаций и обобщается понятием случайной функции. Значение случайной функции в каждый конкретный момент времени является случайной величиной. Следовательно, случайная функция представляет собой совокупность случайных величин. В связи с этим дать ее полную характеристику в виде аналитической зависимости не представляется возможным. В практических задачах пользуются неполной характеристикой случайной функции, представленной такими понятиями как: математическое ожидание, дисперсия, корреляционная функция.
|
|
|
Математическим ожиданием случайной функции X(t) называется такая неслучайная функция mx(t), значение которой в каждый конкретный момент времени t совпадает со средним значением случайной функции X(t) в этот момент времени
mx(t) = M[X(t)].
Таким образом, математическое ожидание mx(t) случайной функции X(t) характеризует изменение во времени ее среднего значения.
Разность между случайной функцией и ее математическим ожиданием называют центрированной случайной составляющей случайной функции
X0(t) = X(t) - mx(t).
Дисперсией случайной функции X(t) называют математическое ожидание квадрата ее центрированной случайной составляющей
DX(t) = D[X(t)] = M {[X0(t)]2}.
Дисперсия случайной функции характеризует разброс возможных реализаций функции относительно математического ожидания. Дисперсия определяет ширину полосы, которой ограничены возможные реализации случайной функции X(t).
Среднее квадратическое отклонение случайной функции связано с дисперсией следующей зависимостью
sx(t) = [Dx(t)]1/2.
Корреляционная функция случайной функции X(t) есть неслучайная функция двух аргументов R(t, t1), которая при каждой паре значений t и t1 равна математическому ожиданию произведения значений центрированной составляющей в эти моменты времени
RX(t,t1) = M [X0(t)×X0(t1)].
Эта зависимость характеризует степень связи между двумя сечениями случайной функции X(t).
Если положить t = t1, то корреляционная функция R(t, t1) обращается в дисперсию Dx(t) случайной функции X(t)
|
|
|
RX(t,t1) = M [X02(t)] = DX(t).
Для определения степени связи между двумя случайными функциями X(t) и Y(t) пользуются взаимно корреляционной функцией
RXY(t,t1) = M [X0(t) × Y0(t)].
Если математическое ожидание и дисперсия случайной функции постоянны, а корреляционная функция зависит только от интервала времени Q = t1 - t, то случайная функция называется стационарной. Следовательно, для стационарной случайной функции:
mx(t) = mx = const; Dx(t) = Dx = const; Rx(t, t1) = Rx(t1 - t) = R(Q).
Поскольку DX(t) = R(t1- t), то для стационарной случайной функции
DX = R(t1- t) = R(0).
Требование постоянства значения математического ожидания для стационарной случайной функции в большинстве ситуаций несущественна, т.к. ее можно центрировать и получить случайную функцию с mx = 0. Таким образом, единственным условием стационарности функции можно назвать следующее выражение
RX(t,t1) = RX(t1- t) = RX(Q).
При анализе случайных процессов пользуются гипотезой эргодичности.
Гипотеза предполагает, что любая статистическая характеристика, полученная усреднением по множеству наблюдений, с вероятностью близкой к единице совпадает с характеристикой, полученной усреднением по времени наблюдения случайного процесса.
Данное положение считают очевидным, даже если оно не доказано. Применение на практике эргодической гипотезы позволяет получить характеристики случайного процесса всего лишь по одной реализации достаточной продолжительности.
Для эргодических случайных процессов применимы следующие зависимости:
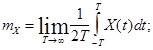
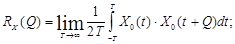

Для стационарных случайных функций вводится еще одно понятие спектральная плотность, характеризующая частотный состав функции. С математической точки зрения спектральная плотность есть Фурье-преобразование корреляционной функции
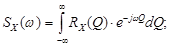
Соответственно, обратное преобразование Фурье дает возможность найти корреляционную функцию по спектральной плотности:
 (1)
(1)
Дисперсия случайной функции связана со спектральной плотностью следующим выражением:
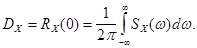 (2)
(2)
Два случайных процессов X(t) и Y(t) могут характеризоваться (аналогично корреляционной) взаимной спектральной плотностью
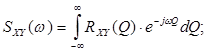
и взаимной корреляцией
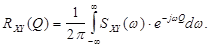
Преобразование стационарного случайного сигнала линейной
Динамической системой
|
|
|
Пусть на линейную систему, имеющую передаточную функцию W(p), действует стационарный случайный сигнал X(t) с математическим ожиданием mx(t) и корреляционной функцией Rx(Q). На выходе системы сигнал Y(t) будет также случайным с математическим ожиданием mx(t) и корреляционной функцией Ry(Q) в установившемся режиме. Поскольку mx(t) - неслучайная функция времени, то my (t) находится обычным для неслучайных сигналов способом:
my(p) = W(p)×mx(p),
где my(p) = L{m Y(t)}; mx(p) = L{mx(t)}.
Корреляционную функцию стационарного случайного сигнала на выходе системы можно вычислить в соответствии с выражением
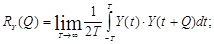 (3)
(3)
На основании уравнения свертки можно получить:
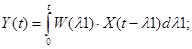 (4)
(4)
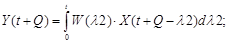 (5)
(5)
где W(l) = L{W(p)} - весовая функция системы.
Стационарный сигнал на выходе системы, который устанавливается при T®¥, определяется путем замены верхних пределов интегрирования в (4) и (5) на ¥ и подстановки этих выражений в уравнение (3)
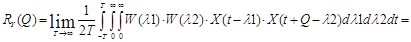
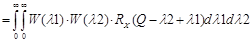 (6)
(6)
Из уравнения (6) можно найти корреляционную функцию случайного сигнала на выходе системы по известной корреляционной функции входного сигнала.
Связь корреляционной функции RY(Q) и спектральной плотности SY(w) выходного сигнала характеризуется выражением
 (7)
(7)
Если выражение RY(Q) из уравнения (6) подставить в (7) и учесть, что


W(jw) × W(-jw) = | W(jw) |2,
то выражение (7) принимает вид:
SY(w) = | W(jw) |2 × SX(w).
Дисперсия на выходе системы вычисляется по формуле:
 (8)
(8)
Если подынтегральное выражение формулы (8) представить в виде:

где A(jw) = a0(jw)n+a1 (jw)n-1+...+an-1 (jw)+an;
G(jw) = b0(jw)2n-2+b1(jw)2n-4+...+bn-2(jw)2+bn,
то в общем случае для устойчивой системы при любом n интеграл
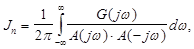
может быть вычислен по формуле
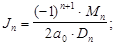 (9)
(9)
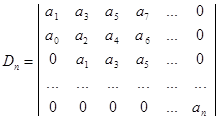 ;
;

|
|
|


