 |
Экспериментальное определение дисперсии.
|
|
|
|
В данной лабораторной работе сигнал ошибки e(t) проходит через квадратор, на выходе которого получается сигнал e2(t). Затем этот сигнал поступает на вход апериодического звена с постоянной времени Т.
Сигнал на выходе апериодического звена можно описать функцией:

где exp(-t/T)/T = L-1{ 1/(Tp+1) } - весовая функция апериодического звена.
При T®¥ предел функции f(e) определяется следующей зависимостью:

Положив верхний предел равным Т и переобозначив переменную интегрирования, можно получить
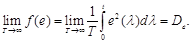
Таким образом, если постоянная времени апериодического звена T®¥, то на его выходе получается значение дисперсии ошибки De. Но, так как время наблюдения и постоянная времени не могут быть бесконечными, то фактически на выходе апериодического звена получается приближенная оценка дисперсии

Если время наблюдения выбрать равным постоянной времени Т, которая определяется из условия
T ³ 50/wн,
где w н - низшая частота спектра случайного сигнала e2(t), то точность вычисления дисперсии составит примерно 2%, что вполне достаточно для практики. За низшую частоту спектра принимают частоту полезного сигнала w0 = 6 c-1. Тогда необходимая постоянная времени апериодического звена Т = 10 с, что и реализовано в лабораторном стенде.
Порядок выполнения работы
1.Рассчитать и построить график зависимости дисперсии ошибки De от постоянной времени интегрирующего элемента модели объекта управления Т02. Определить ее оптимальное значение Т02опт, при котором достигается минимум дисперсии De и само значение дисперсии Demin. Результаты расчетов поместить в протокол.
2.Собрать схему моделирования (рис. 4.5). Задать следующие значения параметров моделируемой системы:
|
|
|
Кпе = 0,1; (Сп = 0,1); Кое = 10,0; (C0 = 1); Т01 = 0; Cn = 0,15;
A = 7 B (значение амплитуды A измеряется в точке g с помощью осциллографа).

3.Снять экспериментально зависимость дисперсии ошибки от постоянной времени, изменяя ее с помощью переключателя от 0,01с до 1с. Экспериментальные данные поместить в протокол.
4.Пронаблюдать во время эксперимента и объяснить изменение характера сигнала ошибки e(t) и параметра De при изменении постоянной времени Т02 в случае нулевого сигнала задающего воздействия (g(t) = 0).
Аналогичный эксперимент следует провести при нулевом значении сигнала помехи (N(t) = 0).
Методика выполнения работы
1.При задании коэффициентов передачи Кпе= Кп×Сп; Кое= К0×С0 следует учитывать, что коэффициенты имеют значения Кп= 1; К0= 10.
2.При подготовке схемы моделирования следует отключить ненужные блоки, установив потенциометры Сi в положение нулевого коэффициента передачи. Тумблеры в цепях обратной связи модели объекта управления, выходного сигнала управляющего устройства и блока задания начальных условий следует поставить в нижнее положение.
3.Величина амплитуды задающего воздействия измеряется в точке «g» осциллографом.
4.Отсчет дисперсии производить не менее, чем через 30 с после подачи команды «ПУСК». Отсчет времени можно осуществлять по встроенному секундомеру.
Содержание отчета
1. Структурная схема исследуемой системы.
2. Теоретический расчет и график зависимости De(T02).
3. Таблица экспериментальных данных
и экспериментальный график De(T02).
4.Выводы по результатам работы:
а) Основные характеристики случайной функции: математическое ожидание, корреляционная функция, спектральная плотность.
б) Преобразование стационарной случайной функции линейной системой.
в) Вычисление дисперсии ошибки.
г) Экспериментальное определение дисперсии.
д) Объяснить влияние параметров системы на величину дисперсии ошибки.
|
|
|
ЛИТЕРАТУРА
1. Юревич Е.И. Теория автоматического управления. - Л.: Энергия, 1975.
2.Воронов А.А., Титов В.К., Новогранов Б.И. - М.: Высшая школа, 1977.
|
|
|


