 |
Показатель демпфирования в объекте второго порядка
|
|
|
|
Лабораторная работа № 8
Изучение инструментария Simulink
Цель работы: На простейшем примере дифференциальных уравнений первого и второго порядка освоить этапы подготовки и моделирования объектов регулирования.
Краткая теория
Постановка задачи
Большинство объектов регулирования могут быть описаны линейными дифференциальными уравнениями с постоянными коэффициентами. На примере объекта, описываемого дифференциальным уравнением второго порядка, рассмотрим все этапы моделирования и анализа свойств объекта. Возьмем, к примеру, объект, у которого входным воздействием является расход пара un, кг/час, а выходная величина - температура x, 0С, рис.1.
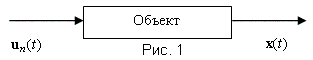
Допустим, что в результате экспериментов по исследованию динамики объекта получено следующее дифференциальное уравнение, описывающее изменение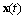 
в зависимости от изменения возмущающей функции 
:
.
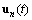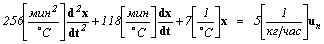Возмущающая функция 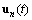должна быть известной функцией времени. Должны быть заданы также начальные условия. Предположим, известно, что в начальный момент времени температура объекта была равна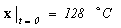 
и происходило остывание со скоростью ]
.
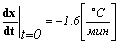Таким образом, необходимо решить на ЭВМ следующее уравнение:
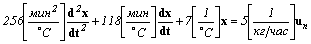
| (1.1) |
при начальных условиях:
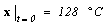
| (1.2) |
 .
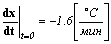| (1.3) |
Метод понижения порядка производной
Решить дифференциальное уравнение - значит получить функцию x(t), меняющуюся во времени. Для составления структурной схемы решения применим метод понижения порядка производной, который сводится к пяти этапам.
Этап I. Разрешим дифференциальное уравнение (1.1) относительно высшей производной
 .
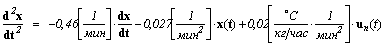| (1.4) |
|
|
|
Этап II: Предположив (рис. 2), что в точке А значение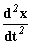 
известно в любой момент времени, с помощью интегрирующего звена и с учетом начальных условий получим в точке В значение 
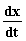. Затем, с помощью еще одного интегратора, в точке С получим значение искомой функции 
.
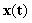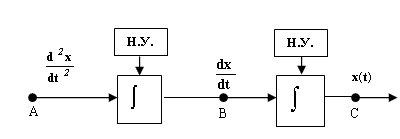
Рис. 2
Этап III. Обратим теперь внимание на правую часть уравнения (1.4). Она представляет собой сумму трех функций времени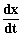 
, 
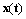и 
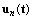, взятых с постоянными коэффициентами. Функция 
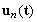- известная функция времени по условию задачи.
Допустим, рис. 3, что нам известны функции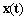 
в точке С1 и 
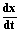в точке В1. Теперь, просуммировав их с коэффициентами, соответствующими правой части (1.4), получим вторую производную 
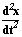. Таким образом, на выходе сумматора, в точке A1, будет величина 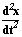, известная в любой момент времени.
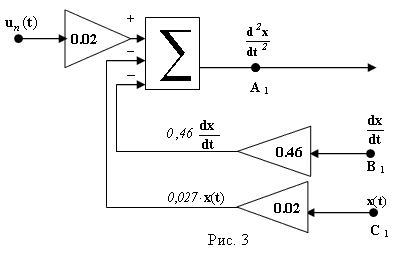
Этап IV. Равенство (1.4), которое происходит из физической сущности моделируемого объекта, требует, чтобы оно (это равенство) выполнялось в каждый момент времени t. Реализовать это требование легко, - достаточно замкнуть схемы, показанные на рис. 2 и 3. При этом сольются: точки А и А1, В и В1 , С и С1 (рис. 4).
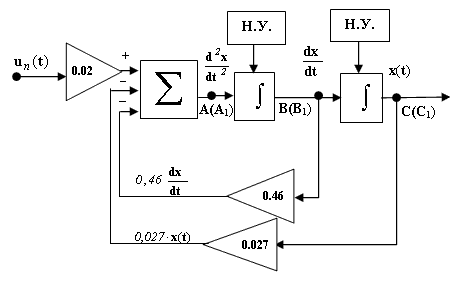
Рис. 4
Этап V. Установить начальные условия, которые определяют единственность решения дифференциального уравнения.
Инструментарий Simulink пакета MatLab как раз и позволяет моделировать и исследовать поведение систем, описываемых любыми (линейными, линейными с переменными коэффициентами и нелинейными) дифференциальными уравнениями. Единственное требование к дифференциальным уравнениям - они должны быть представимы в виде структурных схем, подобных указанной на рис. 4.
Показатель демпфирования в объекте второго порядка
Линейное дифференциальное уравнение можно записать в виде передаточной функции как отношение преобразованного по Лапласу выходного сигнала к преобразованному по Лапласу входному сигналу. Для уравнения (1.1) передаточная функция будет иметь вид
|
|
|
.
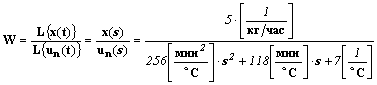Для приведения передаточной функции к каноническому виду разделим числитель и знаменатель на коэффициент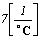 
 .
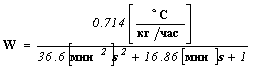| (1.5) |
В общем случае линейному дифференциальному уравнению второго порядка соответствует передаточная функция вида
 ;
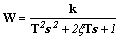| (1.6) |
где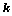 
-коэффициент усиления;
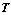- постоянная времени;
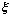- коэффициент относительного затухания (показатель демпфирования).
Заданное уравнение (1.5), приведенное к стандартному виду (1.6), станет следующим:
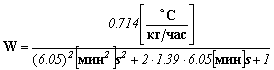
| (1.7) |
· Условие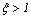 
, например 
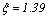как в уравнении (1.7),
означает, что корни характеристического уравнения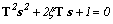 
являются вещественными и (1.6) описывает апериодическое (неколебательное) звено второго порядка. Такое звено может быть представлено как последовательное соединение двух апериодических звеньев первого порядка
 .
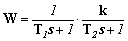| (1.8) |
· При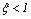 
корни характеристического уравнения комплексные, и передаточная функция описывает колебательное звено второго порядка, которое не может быть представлено в форме (1.8), а только в форме (1.6).
· При 
в уравнении (1.8)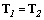 
и корни характеристического уравнения действительные и кратные. Передаточную функцию в этом случае можно записать
 .
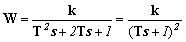| (1.9) |
Малейшее уменьшение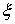 
по отношению к 1, например 
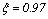, приводит к появлению двух комплексных сопря женных корней характеристического уравнения и такойобъект становится колебательным.
· Случаю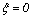 
соответствует колебательное звено второго порядка консервативного типа, которое является идеальным случаем, когда рассеиванием энергии в системе можно пренебречь. Переходные характеристики такого звена представляют собой незатухающие колебания.
· Если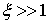 
, то свойства звена приближаются к свойствам звена первого порядка. Например, если
 ,
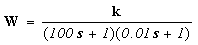| (1.10) |
то объект без потери точности может описываться передаточной функцией
 .
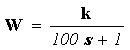| (1.11) |
Единственное отличие будет наблюдаться в самом начале переходного процесса. Какое это отличие, вам следует выяснить самим, проведя моделирование и, может быть, потом обосновать их (эти отличия) аналитически.
|
|
|
