 |
Приложения производной к решению физических задач
|
|
|
|
Как известно, производная характеризует мгновенную скорость прямолинейного движения. Однако этим не исчерпывается использование производной. При изучении неравномерно меняющихся величин скорость их изменения всегда выражается с помощью производной.
Понятие скорости, заимствованное из физики, удобно при исследовании поведения любой функции. Какую бы зависимость ни выражала функция  , отношение
, отношение  есть средняя скорость изменения функции
есть средняя скорость изменения функции  относительно изменения аргумента
относительно изменения аргумента  , а
, а  – мгновенная скорость изменения функции
– мгновенная скорость изменения функции  при некотором значении
при некотором значении  .
.
Так как в практических приложениях нас обычно интересует не только сама функция, но и скорость её изменения, то производная, будучи характеристикой скорости изменения функции, имеет самые широкие практические применения в вопросах физика, химии, геометрии и т.д. Приведём некоторые конкретные примеры использования понятия производной при определении скорости различных процессов.
1. Предположим, что в момент времени t масса ещё не распавшегося радиоактивного вещества была равна m, а через некоторое время, в момент  , асса его уменьшилась (так как часть вещества превратилась в продукт распада) и стала равна
, асса его уменьшилась (так как часть вещества превратилась в продукт распада) и стала равна  (здесь
(здесь  отрицательно, поскольку масса радиоактивного вещества с течением времени уменьшается). Таким образом, за время
отрицательно, поскольку масса радиоактивного вещества с течением времени уменьшается). Таким образом, за время  масса имевшегося радиоактивного вещества изменилась на
масса имевшегося радиоактивного вещества изменилась на  .
.
Отношение 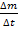 представляет собой среднюю скорость распада за промежуток времени
представляет собой среднюю скорость распада за промежуток времени  . Чем меньше этот промежуток, тем точнее указанное отношение выражает мгновенную скорость распада. Поэтому можно сказать, что мгновенная скорость распада в момент времени t равна
. Чем меньше этот промежуток, тем точнее указанное отношение выражает мгновенную скорость распада. Поэтому можно сказать, что мгновенная скорость распада в момент времени t равна  .
.
2. Мгновенная мощность есть производная  , где
, где  - работа, совершаемая за время
- работа, совершаемая за время  .
.
|
|
|
3. Если V – объем жидкости, на который действует внешнее давление Р, то производная  , дает коэффициент сжатия жидкости при данном давлении.
, дает коэффициент сжатия жидкости при данном давлении.
4. Если твердое тело вращается вокруг оси, то угол поворота  есть функция от времени t. Угловая скорость вращения в данный момент t численно равно производной
есть функция от времени t. Угловая скорость вращения в данный момент t численно равно производной  .
.
5. Сила тока есть производная  , где
, где  – положительный электрический заряд, переносимый через сечение проводника за время
– положительный электрический заряд, переносимый через сечение проводника за время  .
.
6. Теплоемкость при температуре Т есть производная  , где
, где  – количество теплоты, необходимое для измерения температуры на
– количество теплоты, необходимое для измерения температуры на  .
.
Задачи с решением
373. В какой точке касательная к кривой  : а) параллельна оси
: а) параллельна оси  ; б) образует с осью
; б) образует с осью  угол
угол  ?
?
Решение. а) Так как прямая параллельна оси  , то она образует с ней угол 0 и её угловой коэффициент, равный тангенсу этого угла, равен нулю. Известно, что производная функции в данной точке равна угловому коэффициенту касательной к кривой в этой точке, т.е.
, то она образует с ней угол 0 и её угловой коэффициент, равный тангенсу этого угла, равен нулю. Известно, что производная функции в данной точке равна угловому коэффициенту касательной к кривой в этой точке, т.е. 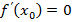 .
.
Найдём производную функции  ; имеем
; имеем  . Тогда
. Тогда  , т.е.
, т.е.  , откуда
, откуда  . Итак, касательная к данной кривой параллельна оси
. Итак, касательная к данной кривой параллельна оси  в точке
в точке  (рис. 103).
(рис. 103).
б) Поскольку прямая образует с осью  угол
угол  , её угловой коэффициент, равный тангенсу этого угла, равен единице. Ранее мы нашли производную функции
, её угловой коэффициент, равный тангенсу этого угла, равен единице. Ранее мы нашли производную функции  в любой её точке:
в любой её точке:  . Найдём значение аргумента, при котором эта производная равна 1:
. Найдём значение аргумента, при котором эта производная равна 1:  , т.е.
, т.е. 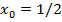 . Тогда
. Тогда  . Итак, касательная к данной кривой составляет с осью
. Итак, касательная к данной кривой составляет с осью  угол
угол  в точке (1/2; -3/4) (рис. 103).
в точке (1/2; -3/4) (рис. 103).
374. Найти угловой коэффициент касательной, проведённой к кривой  в точке
в точке 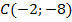 .
.
Решение. Найдём производную функции  в точке
в точке  :
:
 ;
;  .
.
Итак, угловой коэффициент касательной к кривой  в точке
в точке 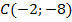 равен 12 (рис. 104).
равен 12 (рис. 104).
375. Кривая задана уравнением 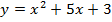 . Определить углы наклона касательных к положительному направлению оси
. Определить углы наклона касательных к положительному направлению оси  , проведённых к кривой в точках с абсциссами
, проведённых к кривой в точках с абсциссами  и
и  .
.
Решение. Найдём производную:  . Обозначив угол наклона касательной в точке с абсциссой
. Обозначив угол наклона касательной в точке с абсциссой  через
через  , а в точке с абсциссой
, а в точке с абсциссой  - через
- через 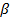 , получим
, получим
|
|
|
 ,
, 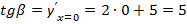 ,
,
Откуда  (или в градусной мере
(или в градусной мере  ), а
), а  . По таблицам тригонометрических функций можно найти и градусную меру угла
. По таблицам тригонометрических функций можно найти и градусную меру угла  .
.
376. На кривой  найти точку, в которой касательная: а) параллельна прямой
найти точку, в которой касательная: а) параллельна прямой  ; б) перпендикулярна прямой
; б) перпендикулярна прямой  .
.
Решение. Пусть искомая точка касания есть 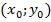 . Тогда, как известно, угловой коэффициент
. Тогда, как известно, угловой коэффициент 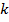 касательной равен значению производной в точке касания, т.е.
касательной равен значению производной в точке касания, т.е.

 .
.
Учитывая это, рассмотрим каждое уз условий задачи.
а) Для того чтобы касательная была параллельна прямой  , их угловые коэффициенты должны совпадать, т.е.
, их угловые коэффициенты должны совпадать, т.е.  или
или  . Решая последнее уравнение относительно
. Решая последнее уравнение относительно  , получим:
, получим: 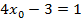 ;
;  ;
;  . Подставляя найденное значение абсциссы искомой точки в уравнение кривой, найдём значение её ординаты:
. Подставляя найденное значение абсциссы искомой точки в уравнение кривой, найдём значение её ординаты:  . Итак,
. Итак,  - искомая точка.
- искомая точка.
б) Из аналитической геометрии известно, что угловые коэффициенты взаимно перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку. Так как угловой коэффициент прямой  равен ¼, то угловой коэффициент
равен ¼, то угловой коэффициент 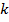 искомой касательной равен
искомой касательной равен  , и мы имеем уравнение
, и мы имеем уравнение  , откуда
, откуда  , т.е.
, т.е.  . Соответственно находим
. Соответственно находим  . Следовательно, точка (1/4; 7/4) – искомая.
. Следовательно, точка (1/4; 7/4) – искомая.
377. Найти углы, под которыми парабола  пересекает ось абсцисс (рис. 105).
пересекает ось абсцисс (рис. 105).
Решение. Найдём абсциссы точек пересечения параболы с осью  , для чего решим уравнение
, для чего решим уравнение  , откуда
, откуда  и
и  . Углом кривой с осью
. Углом кривой с осью  называют угол, который касательная, проведённая в точке пересечения кривой с осью
называют угол, который касательная, проведённая в точке пересечения кривой с осью  , образует с положительным направлением этой оси. Вычислим угловые коэффициенты касательных к параболе в точках
, образует с положительным направлением этой оси. Вычислим угловые коэффициенты касательных к параболе в точках  и
и  . Находим производную:
. Находим производную:  , откуда
, откуда 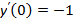 и
и  . Итак,
. Итак,  и
и  , т.е.
, т.е.  и
и  .
.
378. Под каким углом парабола  пересекается с прямой
пересекается с прямой  ?
?
Решение. Этот вопрос может быть сформулирован иначе: под каким углом пересекаются касательные к кривой  , проведённые в точках её пересечения с прямой
, проведённые в точках её пересечения с прямой  , и сама эта прямая?
, и сама эта прямая?
Находим точки пересечения параболы  и прямой
и прямой  , для чего решаем систему уравнений
, для чего решаем систему уравнений  ,
,  . Подставляя
. Подставляя  в первое уравнение, имеем
в первое уравнение, имеем  или
или  , т.е.
, т.е.  ,
,  / Отсюда получим
/ Отсюда получим  ,
,  (рис. 106).
(рис. 106).
Мы нашли две точки пересечения параболы  и прямой
и прямой  :
:  1/2) и
1/2) и  . Найдём производные функции
. Найдём производные функции  в этих точках:
в этих точках:
 =
=  ;
;  ;
;  .
.
Следовательно, угловой коэффициент касательной  , проведённой к кривой
, проведённой к кривой  в точке
в точке  1/2), равен 1, а угловой коэффициент касательной
1/2), равен 1, а угловой коэффициент касательной  в точке
в точке  равен 2. Найдём углы между этими касательными и прямой
равен 2. Найдём углы между этими касательными и прямой  . Уравнение прямой
. Уравнение прямой  можно записать в виде
можно записать в виде  . Таким образом,
. Таким образом,  .
.
|
|
|
Из аналитической геометрии известна формула для нахождения тангенса угла между двумя прямыми по заданным угловым коэффициентам этих прямых:


Итак,  – угол, образованный прямой
– угол, образованный прямой  с касательной
с касательной  , а
, а 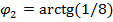 - угол, образованный этой прямой с касательной
- угол, образованный этой прямой с касательной  .
.
379. Составить уравнение касательной к параболе  в точке с абсциссой
в точке с абсциссой  .
.
Решение. Определим ординату  точки касания, подставив в уравнение параболы значение абсциссы
точки касания, подставив в уравнение параболы значение абсциссы  ;
;  .
.
Для нахождения углового коэффициента касательной, вычислим значение производной в точке касания:  . Теперь, зная точку (1;-3) и угловой коэффициент
. Теперь, зная точку (1;-3) и угловой коэффициент 
 , составим уравнение касательной:
, составим уравнение касательной:
 .
.
380. Составить уравнения касательной и нормали к кривой  в точке
в точке  .
.
Решение. Уравнение пучка прямых, проходящих через точку  , имеет вид
, имеет вид 
 . Находим угловой коэффициент касательной:
. Находим угловой коэффициент касательной:

Так как нормаль и касательная, проведённые в одной точке кривой, взаимно перпендикулярны, то угловой коэффициент нормали  . Подставляя полученные значения
. Подставляя полученные значения  и
и  в уравнение пучка прямых, найдём искомые уравнения касательной и нормали:
в уравнение пучка прямых, найдём искомые уравнения касательной и нормали:
уравнение касательной:  или
или  ;
;
уравнение нормали:  или
или  .
.
381. Дана кривая  . Провести к ней касательную в точке, абсцисса которой
. Провести к ней касательную в точке, абсцисса которой  .
.
Решение. Найдём ординату точки касания: 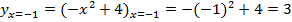 ; значит,
; значит,  – точка касания.
– точка касания.
Уравнение любой прямой, проходящей через точку A, имеет вид  . Для того чтобы прямая была касательной, необходимо и достаточно, чтобы
. Для того чтобы прямая была касательной, необходимо и достаточно, чтобы  . Найдём угловой коэффициент
. Найдём угловой коэффициент 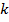 :
:
 .
.
Итак, уравнение касательной имеет вид  , т.е.
, т.е.  .
.
382. В какой точке касательная к кривой  параллельна прямой
параллельна прямой  ?
?
Решение. Угловой коэффициент данной прямой  . Угловой коэффициент касательной
. Угловой коэффициент касательной  .
.
Из условия параллельности следует  . Тогда
. Тогда  ;
; 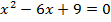 ;
;  . Следовательно,
. Следовательно,  – абсцисса точки касания. Подставляя это значение
– абсцисса точки касания. Подставляя это значение  в уравнение кривой, получим ординату точки касания:
в уравнение кривой, получим ординату точки касания:  .
.
Итак, в точке (3; 10) касательная к данной кривой параллельна прямой  .
.
383. Под каким углом пересекаются кривые 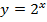 и
и  ?
?
Решение. Найдём точки пересечения данных кривых; решив уравнение  , получим
, получим  ,
,  .
.
Под углом между кривыми понимается угол между касательными в точке пересечения кривых. Величину угла находят, пользуясь известной формулой  , где
, где  – угловые коэффициенты касательных в точке их пересечения.
– угловые коэффициенты касательных в точке их пересечения.
|
|
|
Найдём  ,
,  . Вычислим значения угловых коэффициентов в точках
. Вычислим значения угловых коэффициентов в точках  :
:

Итак, в точке  имеем
имеем
 , откуда
, откуда 
В точке  имеем
имеем
 , т.е.
, т.е.  .
.
405. Путь, пройденный краном, задаётся следующей функцией времени:  . Найти скорость движения крана в конце 5-й секунды.
. Найти скорость движения крана в конце 5-й секунды.
Решение. Находим производную: 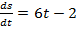 ; при
; при  получим
получим  (м/с).
(м/с).
410. Высота тела, брошенного вертикально вверх, меняется в зависимости от времени по закону  . Найти скорость тела в конце 10-й секунды. Сколько секунд тело будет лететь вверх и какой наибольшей высоты оно достигает?
. Найти скорость тела в конце 10-й секунды. Сколько секунд тело будет лететь вверх и какой наибольшей высоты оно достигает?
Решение. Скорость тела определяется выражением  при
при  имеем
имеем  (м/с).
(м/с).
В тот момент, когда тело достигает максимальной высоты, его скорость равна нулю. Следовательно, для этого момента  , откуда
, откуда  (с).
(с).
Подставляя это значение в уравнение движения, получим наибольшую высоту, на которую поднимается тело:
 (м)
(м)
413. Тело массой 8 кг движется прямолинейно по закону  . Найти кинетическую энергию тела (
. Найти кинетическую энергию тела ( через 3 с после начала движения.
через 3 с после начала движения.
Решение. Найдём скорость движения тела в любой момент времени t:

Вычислим скорость тела в момент времени  :
:
 (м/с).
(м/с).
Определим кинетическую энергию тела в момент времени  :
:
 900 (Дж).
900 (Дж).
433. Точка движется прямолинейно по закону  . Найти скорость и ускорение точки в момент
. Найти скорость и ускорение точки в момент  .
.
Решение. Для определения скорости нужно найти первую производную данной функции при  . Имеем
. Имеем
 (м/с).
(м/с).
Ускорение равно второй производной функции при  , т.е.
, т.е.
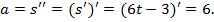
Величина ускорения оказалась постоянной для любого значения t; значит, движение точки по заданному закону происходит с постоянным ускорением.
434. Трактор ДП-150 движется по закону  . Найти её ускорение в конце 3-й секунды.
. Найти её ускорение в конце 3-й секунды.
Решение. Находим  , откуда при
, откуда при  получим
получим  (м/
(м/  .
.
435. В момент времени t машина находится на расстоянии  км от места отправления. Найти его ускорение через 2 ч.
км от места отправления. Найти его ускорение через 2 ч.
Решение. Находим  . При
. При  имеем
имеем  (км/
(км/ 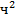 ).
).
440. Точка движется вдоль оси абсцисс по закону  , где t – время в секундах, отсчитываемое от
, где t – время в секундах, отсчитываемое от  , а
, а  - расстояние движущейся точки от начала координат в метрах. Требуется: а) определить закон изменения скорости и ускорения движения от времени t; б) найти начальную скорость и скорость в момент
- расстояние движущейся точки от начала координат в метрах. Требуется: а) определить закон изменения скорости и ускорения движения от времени t; б) найти начальную скорость и скорость в момент  с; в) установить, существуют ли моменты времени, когда скорость равна нулю, и если да, то какие положения движущейся точки соответствуют этим моментам.
с; в) установить, существуют ли моменты времени, когда скорость равна нулю, и если да, то какие положения движущейся точки соответствуют этим моментам.
Решение. а) Для определения скорости движения найдём производную пути по времени:
 ,
,
а для определения ускорения движения – производную скорости по времени:
 .
.
|
|
|
б) Если  , то
, то  (м/с) (начальная скорость); если
(м/с) (начальная скорость); если  , то
, то  (м/с).
(м/с).
в) Условие  означает, что
означает, что  Решая это уравнение, получим
Решая это уравнение, получим 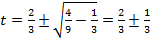 . Следовательно, значение
. Следовательно, значение  достигается дважды: сначала – в момент
достигается дважды: сначала – в момент  1/3 с, а затем – в момент
1/3 с, а затем – в момент  .
.
Найдём абсциссы движущейся точки в эти моменты времени:
 м;
м;  (м).
(м).
441. Тело, масса которого 30 кг, движется прямолинейно по закону 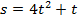 . Доказать, что движение тела происходит под действием постоянной силы.
. Доказать, что движение тела происходит под действием постоянной силы.
Решение. Имеем  Следовательно,
Следовательно,  , т.е. при данном законе движения тело движется с постоянным ускорением 8 м/
, т.е. при данном законе движения тело движется с постоянным ускорением 8 м/  . Далее, так как масса тела постоянна (30 кг), то по второму закону Ньютона действующая на него сила
. Далее, так как масса тела постоянна (30 кг), то по второму закону Ньютона действующая на него сила  (H) – также постоянная величина.
(H) – также постоянная величина.
448. Стороны  и
и  прямоугольника изменяются по закону
прямоугольника изменяются по закону  см,
см,  см. С какой скоростью изменяется его площадь S в момент времени
см. С какой скоростью изменяется его площадь S в момент времени  с?
с?
Решение. Находим  ,
,
 . При
. При  получим
получим  (cм/c).
(cм/c).
453. Маховик за время t поворачивается на угол  (t – в секундах,
(t – в секундах,  в конце 3-й секунды. Найти момент, когда прекратится вращение.
в конце 3-й секунды. Найти момент, когда прекратится вращение.
Решение. Имеем  Так как
Так как 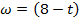 рад/с, то при
рад/с, то при  получим
получим  (рад/с). Вращение прекратится в момент, когда
(рад/с). Вращение прекратится в момент, когда  , т.е. при t=8 c.
, т.е. при t=8 c.
455. Количество электричества, протекающее через проводник, начиная с момента времени  , задаётся формулой
, задаётся формулой  . Найти силу тока в конце 6-й секунды.
. Найти силу тока в конце 6-й секунды.
Решение: Сила тока есть производная количества электричества по времени: следовательно, нужно найти производную функции  и вычислить её значении при
и вычислить её значении при  с. Имеем
с. Имеем  , откуда при
, откуда при  получим
получим  (A).
(A).
460. Количество теплоты Q, получаемое некоторым веществом при нагревании его от 0 до T, определяется по формуле  (Q – в джоулях, T – в кельвинах). Найти теплоёмкость этого вещества при 100 K.
(Q – в джоулях, T – в кельвинах). Найти теплоёмкость этого вещества при 100 K.
Решение. Находим теплоёмкость:
 .
.
При T = 100 K получим
 (Дж/К).
(Дж/К).
461. Закон изменения температуры T тела в зависимости от времени t задан уравнением  . C какой скоростью нагревается это тело в момент времени 10 с?
. C какой скоростью нагревается это тело в момент времени 10 с?
Решение. Скорость нагревания тела есть производная температуры T по времени t:
 .
.
Определим скорость нагревания тела при  :
:
 (град/с).
(град/с).
|
|
|


