 |
Прозрачная распределённая обработка.
|
|
|
|
Операционная система QNX Neutrino предоставляет системную службу под названием «прозрачная распределённая обработка» (transparent distributed processing — TDP), которая обеспечивает приложениям прозрачный доступ к драйверам устройств, сетевым стекам и другим системным службам, работающим на других узлах сети. При наличии соответствующих прав доступа любой процесс может воспользоваться почти любым удалённым ресурсом так, как если бы этот ресурс работал на локальном процессоре.
Прозрачность расположения системных служб упрощает проектирование отказоустойчивых систем с выравниванием загрузки. Предположим, к примеру, что компьютер предоставляет вычислительные службы клиентским приложениям через сеть. В случае отказа этого компьютера и запуска резервного компьютера клиентские приложения не требуют ни осведомления о том, что обработка их запросов выполняется новым компьютером, ни специального программирования для установления соединения с этим компьютером. Все сообщения, которые посылают клиентские приложения, автоматически направляются новому адресату.
Механизм распределённой обработки компании QNX также сокращает затраты на оборудование. Например, если одно устройство автомобильной информационно-развлекательной системы оснащено Bluetooth-соединением, то другим устройствам не требуется иметь собственный Bluetooth-стек и трансиверный чип, поскольку они могут воспользоваться существующим соединением [7].
Отказоустойчивое сетевое взаимодействие.
Механизм распределённой обработки операционной системы QNX Neutrino, который обеспечивает абстрагирование от сети, делает возможным прозрачное взаимодействие приложений через резервные сетевые линии: при отказе одной линии операционная система автоматически перенаправляет трафик на другие. Кроме того, можно выравнивать загрузку всех сетевых линий, что повышает пропускную способность сети. Как и в случае с распределённой обработкой, приложения получают преимущества отказоустойчивого сетевого взаимодействия без написания специального кода [7].
|
|
|
Меньшее потребление памяти.
Поскольку микроядерная архитектура ОСРВ QNX Neutrino обладает масштабируемостью на уровне системных компонентов, QNX Neutrino обеспечивает значительно более компактную среду исполнения, чем ОС Linux. Это является важнейшим преимуществом для таких крупносерийных устройств, как мультимедийные и автомобильные телематические системы, в которых удешевление памяти на 2 доллара приносит миллионы долларов дополнительной прибыли. Собственная оконная система ОС QNX Neutrino, QNX Photon® microGUI®, также использует микроядерную архитектуру, что позволяет проектировщикам без труда «отключать» службы графического пользовательского интерфейса, которые не требуются в устройствах с ограниченным объёмом памяти [7].
Сравнение параметров операционных систем реального времени.
Сравнение параметров операционных систем реального времени представлено в приложении «А».
Как мы видим у операционной системы реального времени QNX много достоинств, так как она построено на микроядерной архитектуре, эта архитектура дает высокую стабильность работы с меньшими задержками, это ставит ее на первое место для наших задач перед другими операционными системам реального времени с монолитным ядром К тому же эта система хорошо документирована, есть бесплатные средства разработки, легком масштабируется без прерывания работы. Ценовая политика для телеком компаний изменилась в 2012 году, систему можно купить за меньшие деньги, или попробовать бесплатно в некоммерческих целях [10].
|
|
|
Предоставление «жесткого» реального времени аппаратными средствами.
Помимо операционной системы реального времени мы можем использовать специализированные сетевые карты для получения более точных временных меток. Например Intel® Ethernet Server Adapter I340 (основанная на Intel® 82580 Gigabit Ethernet Controller и поддерживающая стандарт IEEE 1588 принимает пакеты и на аппаратном уровне устанавливает на них временные метки с точностью от 3 до 7 нано-секунд), Silicom PE2Gi80, Neterion X3110/X3120 (10 Gbit) [9].
Но такие сетевые карты очень дороги и для наращивания возможностей приходится каждый раз платить большую сумму, что нам не подходит.
Критерии согласия.
Используя выбранные технические средства можно будет измерять интервалы между поступлениями заявок, получать функцию распределения длительности интервалов между поступлениями заявок, обычно для дальнейших вычислений (например, оценки требуемой пропускной способности, нужной для обслуживания с заданным уровнем качества) полученную на практике функцию заменяют теоретическим распределением, для этого используются критерии согласия.
Для проверки соответствия эмпирического распределения теоретическому (гипотезы) можно наложить на гистограмму теоретическую кривую (рисунок 3.6) [8].
Рисунок 3.6 - Гистограмма и теоретическая плотность распределения
При этом неизбежно обнаружатся расхождения, либо случайные, связанные с ограниченным объемом наблюдений, либо свидетельствующие о неправильном подборе выравнивающей функции (гипотезы). Для ответа на этот вопрос используют так называемые «критерии согласия». Для этого вводится случайная величина U, характеризующая расхождение эмпирического и теоретического распределений в предположении истинности теоретического распределения. Мера расхождения U выбирается таким образом, чтобы функция ее распределения 
не зависела от вида выравниваемого (эмпирического) распределения и достаточно быстро сходилась по числу наблюдений n к предельной функции F(U). Затем определяется фактическая степень расхождения u и оценивается вероятность [8]
(3.1)
Малая величина 
говорит о том, что полученное расхождение u в силу чисто случайных причин маловероятно, и теоретическое распределение плохо согласуется с эмпирическим. Однако, большие вероятности не могут считаться исчерпывающим доказательством истинности теоретического закона распределения и свидетельствуют лишь об отсутствии оснований его отвергнуть.
|
|
|
Иногда поступают иначе: заранее рассчитывают меру расхождения û, которая может быть превышена с указанной малой вероятностью, и при u > û рассматриваемое теоретическое распределение отвергают.
Существует множество критериев согласия, среди которых наиболее употребительными являются критерий 
Пирсона и критерий Колмогорова-Смирнова.
В критерии согласия Пирсона мерой расхождения теоретического и эмпирического распределений является взвешенная сумма квадратов отклонений
(3.2)
где k – число интервалов разбиения значений случайной величины, 
– количество наблюдений, попавшее в i-й интервал, 
– теоретическая вероятность появления значения из i-го интервала, n – общее число наблюдений [8].
В практических задачах рекомендуется иметь в каждом интервале разбиения не менее 5-10 наблюдений.
Обозначим через t число независимых связей, наложенных на вероятности –. Их общее число равно количеству характеристик теоретического распределения, подбираемых по опытным данным, плюс единица (условие нормировки 
). Таким образом, схема применения критерия 
к оценке согласованности теоретического и эмпирического распределений сводится к следующему [8]:
· Определяется мера расхождения по формуле.
· Определяется число степеней свободы r = k – t.
· По r и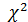 
с помощью специальной таблицы определяется вероятность того, что величина, имеющая распределение с r степенями свободы, превзойдет данное значение . Если эта вероятность весьма мала, гипотеза (теоретическая кривая) отбрасывается как неправдоподобная. Если же эта вероятность относительно велика, гипотезу можно признать не противоречащей полученным экспериментальным данным.
Насколько мала должна быть вероятность р для того, чтобы отбросить или пересмотреть гипотезу, не решается на основе математических соображений и выкладок. На практике, если оказывается, что р < 0.1, рекомендуется проверить или повторить эксперимент. Если заметные расхождения появятся снова, следует искать другой, более подходящий для описания опытных данных закон распределения. Если же вероятность p > 0.1 (относительно велика), то это еще не может считаться доказательством справедливости гипотезы, а говорит лишь о том, что гипотеза не противоречит экспериментальным данным.
|
|
|
В критерии Колмогорова-Смирнова мерой расхождения теоретического F(x) и эмпирического 
распределений является максимальный модуль разности [8]
(3.3)
А.Н. Колмогоров доказал, что при n→∞ независимо от вида F(x) вероятность неравенства [8]
(3.4)
стремится к пределу [8]
(3.5)
Для проверки гипотезы по критерию согласия Колмогорова-Смирнова необходимо построить функции распределения F(x) для теоретического и для эмпирического распределений, определить максимум d модуля разности между ними и найти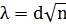 
. После этого следует найти по специальной таблице 3.1. [8] вероятность P(𝜆).
Таблица 3.1 - Вероятность P(𝜆)
| 𝜆 | P(𝜆) | 𝜆 | P(𝜆) | 𝜆 | P(𝜆) |
| 0.0 | 1.000 | 0.7 | 0.711 | 1.4 | 0.040 |
| 0.1 | 1.000 | 0.8 | 0.544 | 1.5 | 0.022 |
| 0.2 | 1.000 | 0.9 | 0.393 | 1.6 | 0.012 |
| 0.3 | 1.000 | 1.0 | 0.270 | 1.7 | 0.006 |
| 0.4 | 0.997 | 1.1 | 0.178 | 1.8 | 0.003 |
| 0.5 | 0.964 | 1.2 | 0.112 | 1.9 | 0.002 |
| 0.6 | 0.864 | 1.3 | 0.068 | 2.0 | 0.001 |
Малая вероятность P(𝜆) свидетельствует о неприемлемости теоретической функции.
В результате исследований в качестве основного критерия согласия для реализации в приложении был выбран критерий Колмогорова-Смирнова.
|
|
|
