 |
Графическое решение модели реактора РИС-Н, работающего адиабатическом режиме, для необратимых эндо- и экзотермических реакций.
|
|
|
|
Кинетическое уравнение необратимой реакции первого порядка имеет вид
 .
.
Подставим его в уравнение (6.12)
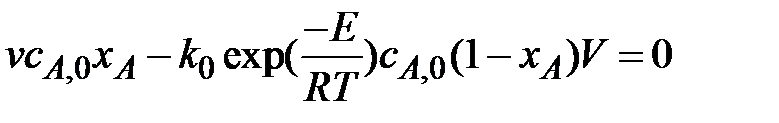 . (6.14)
. (6.14)
Для определения степени превращения хА и температуры Т в реакторе уравнение материального баланса (6.14)нужно решить совместно с уравнением теплового баланса (6.13). Аналитическое решение этой системы уравнений затруднено из-за того, что температура T входит в уравнения и в виде линейного члена, и в составе комплекса, являющегося показателем экспоненциальной функции. Такие уравнения являются трансцендентными, и для их решения применяют численные методы.
Решим систему уравнений (6.13) и (6.14)графическим методом. Для этого запишем оба уравнения в виде зависимостей хА Т,построим графики этих зависимостей и найдем точки их пересечения, удовлетворяющие одновременно обоим уравнениям, т. е. являющиеся решениями системы.
В уравнении теплового баланса (6.14)зависимость между хА и T является линейной.
Эта прямая линия пересекает ось температур в точке Т = Т 0и имеет угловой коэффициент
 (6.15)
(6.15)
Знак углового коэффициента зависит от знака теплового эффекта, он отрицателен для эндотермических реакций, у которых ∆Н > 0 (рис. 1, а),и положителен для экзотермических реакций (рис. 1, б). Крутизну угла наклона можно изменить, меняя начальную концентрацию сA ,0.

Рис. 1. Уравнение теплового баланса реактора идеального смешения
в координатах хА – Т дляэндотермической (а)и экзотермической (б)реакций
Если принять хА = 1 (т. е. реакция прошла до конца), из уравнения (6.15) получим

Величина ∆T АД – максимальное изменение температуры реакционной смеси, возможное в адиабатических условиях, или адиабатическое изменение температуры (для экзотермических реакций, например, адиабатический разогрев). Уравнение (6.15) с учетом ∆T адможно записать так:
|
|
|
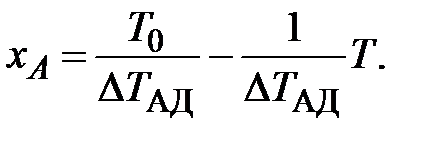 (6.16)
(6.16)
Вид зависимости хА (T), соответствующей уравнению материального баланса (6.12), зависит от типа кинетического уравнения реакции. Для необратимой реакции первого порядка (эндотермической, и экзотермической) уравнение материального баланса (6.12) можно представить в следующем виде (с учетом того, что V/v =  ):
):
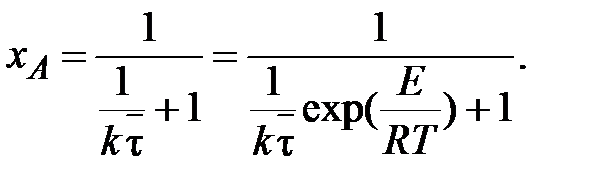 (6.17)
(6.17)
Уравнение (6.17) описывает монотонно возрастающую функцию хa (T). При низких температурах, когда кинетическая энергия молекул существенно ниже энергии активации (об этом можно судить, сравнивая энергии Е и RT), хА 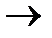 0. При высоких температурах, когда величины Е и RT имеют одинаковый порядок, числовое значение exp[ E /(RT)]невелико. Так как предэкспоненциальный множитель k 0= 108 + 1013, то в этом случае хА
0. При высоких температурах, когда величины Е и RT имеют одинаковый порядок, числовое значение exp[ E /(RT)]невелико. Так как предэкспоненциальный множитель k 0= 108 + 1013, то в этом случае хА  1.
1.
Таким образом, график функции (6.17) – кривая без экстремумов (рис. 2, кривая 1), при низких температурах асимптотически приближающаяся к нулю, при высоких – к единице, а при «средних» температурах имеющая одну точку перегиба (ее координаты можно получить, приравняв нулю производную d 2 xA/dT 2).
Положение среднего участка кривой относительно оси температур можно изменить, увеличив или уменьшив среднее время пребывания в реакторе 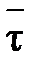 (
(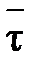 = V/v). Из уравнения (6.17) следует, что увеличение
= V/v). Из уравнения (6.17) следует, что увеличение 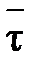 при тех же температурах приведет к росту хА (рис. 2, кривая 2).
при тех же температурах приведет к росту хА (рис. 2, кривая 2).

Рис. 2. Уравнение материального баланса реактора идеального смешения
в координатах хA – Т для необратимой реакции первого порядка при
среднем времени пребывания  1 (1)и
1 (1)и 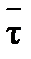 2 (2)
2 (2)
Решение системы уравнений материального и теплового балансов имеет несколько различающийся вид для эндо- и экзотермических необратимых реакций. В случае проведения в адиабатическом реакторе идеального смешения необратимой эндотермической реакции графики функций (6.16) и (6.17) имеют лишь одну точку пересечения (см. рис. 3).
|
|
|
Координаты этой точки (хА/, T/) и являются решением системы уравнений: если в адиабатический реактор идеального смешения заданного объема V подает исходный реагент А, имеющий концентрацию сА ,0 с объемным расходом v и при начальной температуре Т 0,необратимая эндотермическая реакция будет протекать в аппарате при температуре Т и при этом будет достигаться степень превращения хА/.
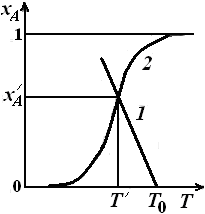
Рис. 3. Уравнения теплового (1) и материального (2)балансов
для адиабатического реактора идеального смешения при проведении
в нем необратимой эндотермической реакции (совместное решение)
Если в адиабатическом реакторе проводят необратимую экзотермическую реакцию, система уравнений материального и теплового балансов может иметь как одно, так и несколько решений, отвечающих стационарному режиму.
Из рис. 4 видно, что графики функций (6.16) и (6.17) имеют только одну точку пересечения, если начальная температура Т 0реакционного потока будет сравнительно низкой (например, Т 10)или сравнительно высокой (например, T 20). При этом оказывается, что при подаче реагентов в реактор с низкой начальной температурой Т 10процесс будет протекать при температуре, мало отличающейся от T 10, а достигаемая степень превращения (ордината точки А на рис. 4) также будет очень низка. Более выгодным является режим работы реактора, соответствующий начальной температуре Т 30.В этом случае также имеется лишь одна точка пересечения графиков (точка Е),т. е. одно решение системы уравнений, но оно соответствует высокой степени превращения, почти равной единице.
Если же реагенты подавать в реактор с начальной температурой Т 20, то линии, соответствующие уравнениям материального и теплового балансов, пересекаются трижды, т. е. координаты точек В, С, D являются возможными решениями системы уравнений, составляющей математическую модель адиабатического реактора идеального смешения.
В таких случаях говорят о множественности стационарных состояний реактора. При этом возникает дополнительная проблема устойчивости рассматриваемых стационарных состояний.
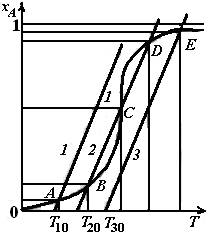
Рис. 4. Уравнения теплового (1, 2, 3) и материального (4)балансов
для адиабатического реактора идеального смешения при проведении
в нем необратимой экзотермической реакции (совместное решение)
|
|
|
|
|
|


