 |
Второй (окружной) этап Всероссийской олимпиады школьников по физике
|
|
|
|
Г. Москва, 2011 г.
Класс
1. Троллейбус начинает разгоняться по прямой дороге с постоянным ускорением a = 0,5 м/с2 без начальной скорости. Велосипедист, находящийся на расстоянии L = 50 м сзади от троллейбуса, начинает догонять троллейбус, двигаясь с постоянной скоростью. Какой должна быть скорость велосипедиста V, чтобы он догнал троллейбус?
Решение. В системе отсчета, связанной с велосипедистом, троллейбус движется к велосипедисту равнозамедленно с ускорением a при начальной скорости V – до остановки в этой системе отсчета он пройдет за время t = V / a расстояние s = at 2/2 = V 2/(2 a). Встреча велосипедиста и троллейбуса произойдет при s ≥ L, или при  ≈ 7 м/с.
≈ 7 м/с.
Ответ: велосипедист догонит троллейбус, если будет двигаться со скоростью  ≈ 7 м/с.
≈ 7 м/с.
2. К концам легкого рычага, который может свободно вращаться вокруг горизонтальной оси, прикреплены две нити, к которым привязаны два шара одинакового радиуса. Когда шары висят в воздухе, рычаг находится в равновесии. Шары опускают в большие сосуды с водой так, что они не касаются стенок и дна сосуда. Первый шар погружается в воду наполовину, второй – полностью. Нити при этом остаются натянутыми, а равновесие рычага в результате не нарушается. Найдите отношение массы первого шара к массе второго шара.
Решение. Пусть l 1 и l 2 – длины плеч рычага, m 1 и m 2 – массы шаров, V – объем каждого из них. Когда шары не погружены в воду, к концам рычага приложены силы m 1 g и m 2 g, и условие равновесия рычага оказывается следующим:
m 1 gl 1= m 2 gl 2.
При погружении шаров в воду плотностью ρ0 на первый (погруженный наполовину) шар будет действовать сила Архимеда ρ0 gV /2, на второй – сила Архимеда ρ0 gV. Следовательно, условие равновесия рычага примет вид
|
|
|
(m 1 g – ρ0 gV /2) l 1= (m 2 g – ρ0 gV) l 2.
Вычитая из первого уравнения второе уравнение, находим: l 1 = 2 l 2. Отсюда с учетом первого уравнения получим: m 1: m 2=0,5.
Ответ: отношение массы первого шара к массе второго шара равно 0,5.
3. В калориметр, содержащий M = 1 кг воды неизвестной начальной температуры, друг за другом бросают одинаковые кубики льда, каждый массой m = 100 г с температурой 0 ºC, дожидаясь каждый раз установления теплового равновесия. Первый и второй кубики растаяли полностью, третий – частично. Четвертый кубик плавиться так и не стал. В каком интервале могла находиться начальная температура воды? Удельная теплота плавления льда λ = 335 кДж/кг, удельная теплоемкость воды c = 4,2 кДж/(кг·ºC).
Решение. Поскольку четвертый кубик плавиться не стал, к моменту опускания этого кубика уже установилась температура 0 ºC. Поэтому количества теплоты cMt 0, выделяющегося при охлаждении воды от неизвестной начальной температуры t 0 до 0 ºC, хватает на полное плавление двух кубиков льда и частичное плавление третьего: оно превосходит 2λ m, но меньше 3λ m:
2λ m < cMt 0 < 3λ m.
Поэтому начальная температура воды t 0 лежит в интервале от 2λ m /(cM)» 16 ºC до 3λ m /(cM)» 24 ºC.
Ответ: начальная температура воды t 0 лежит в интервале от 2λ m /(cM)» 16 ºC до 3λ m /(cM)» 24 ºC.
4. Школьницы Алиса и Василиса нагревают воду в стаканах при помощи кипятильников. Кипятильник Алисы нагревает воду до кипения за t 1 = 6 мин., а кипятильник Василисы – за t 2 = 12 мин. За какое время удастся довести воду в стакане до кипения, если нагревание проводить, используя оба кипятильника? Стаканы с водой одинаковые, потерями энергии пренебречь.
Решение. Пусть Q – количество теплоты, требуемое для доведения до кипения воды в стакане. Тогда мощность кипятильника Алисы равна Q / t 1, мощность кипятильника Василисы равна Q / t 2. Когда кипятильники работают вместе, их общая мощность будет равна Q / t 1 + Q / t 2. Следовательно, вода в этом случае закипит за время
|
|
|
t = Q /(Q / t 1 + Q / t 2) = t 1 t 2/(t 1 + t 2) = 4 мин.
Ответ: воду удастся довести до кипения за время t = t 1 t 2/(t 1 + t 2) = 4 мин.
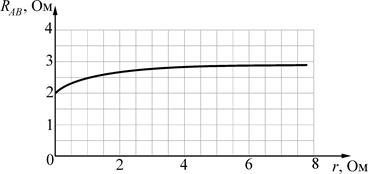
5. Электрическая цепь, изображенная на рисунке 1, состоит из параллельно соединенных резисторов r и R 1, последовательно к которым подключен резистор R 2. Школьник Ярослав исследует зависимость сопротивления RAB данной электрической цепи от сопротивления резистора r. В результате обработки результатов опыта Ярослав получил график, изображенный на рисунке 2. Чему равны сопротивления резисторов R 1 и R 2 электрической цепи?

| 
|
| Рис. 1 | Рис. 2 |
Решение. При r = 0 сопротивление цепи RAB совпадает с R 2. Как показывает график, в этом случае R AB = 2 Ом. Поэтому R 2 = 2 Ом.
При r = 1 Ом из графика получим: RAB = 2,5 Ом. Поскольку RAB = R 2 + 1/(1/ R 1 + 1/ r), находим, что R 1 = 1 Ом.
Для проверки ответа можно рассмотреть случай, когда сопротивление r очень велико – тогда сопротивление цепи должно совпадать с R 1 + R 2 = 3 Ом. Этот результат действительно соответствует графику.
Ответ: R 1 = 1 Ом, R 2 = 2 Ом.
|
|
|


