 |
Второй (окружной) этап Всероссийской олимпиады школьников по физике
|
|
|
|
Г. Москва, 2011 г.
Класс
1. Два небольших блока с неподвижными осями установлены на одной высоте 12 м от земли на краю крыши школы на расстоянии 10 м друг от друга. Через эти блоки перекинута веревка, вертикальные концы которой держат стоящие на земле десятиклассники Вася и Петя. На веревке посередине между этими двумя блоками вставлен еще один блок с подвижной осью. К оси этого третьего блока прикреплен крюк, на который повесили ведро с краской. Когда веревку натянули, ее участки между блоками выпрямились и образовали с вертикалью одинаковые углы. Ведро при этом стояло на земле. Вася, стоя на месте, начинает выбирать веревку со скоростью 0,3 м/с, а Петя, тоже стоя на месте, со скоростью 0,2 м/с. Какой будет скорость ведра через 12 секунд?
Решение. В исходном положении длина участка веревки, расположенного между неподвижным и подвижным блоком, равна 
м. За 12 секунд Вася выберет 0,3×12 = 3,6 м веревки, а Петя выберет 0,2×12 = 2,4 м веревки. Следовательно, суммарная длина участка веревки между неподвижными блоками сократится на 6 м и станет равной 20 м, а расстояние между неподвижным и подвижным блоком станет равным 10 м. Обозначим скорости, с которыми Вася и Петя выбирают веревку, через V 1 и V 2. За малый промежуток времени D t ведро, двигаясь со скоростью V, сместится вертикально вверх на расстояние 
. При этом длина участка веревки между неподвижным и подвижным блоком уменьшится на 
. Из рисунка видно, что 
. Отсюда, учитывая, что a = 30° и 
, получаем: 
м/с.
Ответ: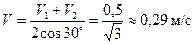 
.
2. Изображённая на рисунке система грузов расположена в лифте, поднимающемся с ускорением a = g/ 10. Трение отсутствует, блок невесом, нити невесомы и нерастяжимы. Оказалось, что ускорения груза m относительно земли и лифта равны по модулю. Найдите отношение масс грузов M/m.
|
|
|
Решение: Обозначим ускорение груза m относительно лифта через a 1. Так как ускорение этого груза относительно лифта a 1 направлено вниз и равно по модулю его ускорению A относительно земли, то ускорение А направлено вверх. Запишем второй закон Ньютона для грузов M и m в проекциях на координатные оси X и Y (см. рисунок) в системе отсчета, связанной с землей:
, 
.
Здесь T – сила натяжения нити, 
– ускорение груза m относительно земли. Решая полученную систему уравнений, находим: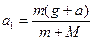 
.
Согласно условию задачи, 
. Отсюда
и 
.
Ответ: 
3. Упругая легкая пружина жесткостью k с длиной в недеформированном состоянии L одним концом прикреплена к неподвижному шарниру, а другим концом – к небольшой муфте массой m, которая может без трения скользить по длинной прямой горизонтальной спице. Расстояние от шарнира до спицы равно L /2. В начальный момент муфта покоится, и пружина не деформирована. Вдоль той же спицы к первой муфте приближается вторая, имеющая массу m /3. Происходит абсолютно упругий удар. При какой скорости второй муфты за мгновение до удара первая будет после удара совершать колебания со средним положением, соответствующим минимально возможному расстоянию от неё до шарнира?
Решение. Так как соударение между муфтами абсолютно упругое, можно применить для него законы сохранения импульса (в проекции на направление спицы) и механической энергии:
, 
.
Здесь V и V ¢ – скорости налетающей муфты до соударения и после соударения, соответственно, V 0 – скорость муфты m после соударения. Решим эту систему уравнений:
.
Отсюда 
, и 
.
Для того чтобы после соударения муфта m совершала колебания со средним положением, соответствующим минимально возможному расстоянию от неё до шарнира, необходимо, чтобы начальная кинетическая энергия муфты оказалось достаточной для того, чтобы пружина сжалась от начальной длины L до минимальной длины L /2. Если начальная кинетическая энергия муфты m окажется большей, то муфта пройдет положение равновесия под шарниром, и возникнут колебания с нужным средним положением. Поэтому из закона сохранения механической энергии следует неравенство: 
. Отсюда, подставляя выражением для V 0, имеем: 
|
|
|
Ответ: Скорость второй муфты должна удовлетворять условию 
4. Вася достал из морозильника пластину льда с размерами 10 см × 10 см × 1 см. Взяв щипцы, он расколол пластину на небольшие кубики с размером ребра 1 см, совершив при этом работу 27 Дж. Оцените минимальную работу, совершения которой было бы достаточно для получения желаемого результата. Чему примерно равен КПД Васи при раскалывании пластины? Энергия молекул, находящихся на поверхности льда, пропорциональна площади поверхности; эта энергия больше энергии молекул, находящихся в объеме. Коэффициент пропорциональности σ» 0,076 Дж/м2.
Решение. Площадь поверхности вынутой из холодильника пластины равна S 0 = 240 см2. Общая площадь поверхности полученных кубиков льда равна S 1 = 600 см2. Следовательно, при раскалывании льда энергия молекул увеличивается на
D E = σ(S 1 – S 0) ≈ 2,7 мДж. Это и есть минимальная работа, которую необходимо совершить для раскалывания ледяной пластины. Следовательно, КПД Васи при раскалывании пластины равен примерно (2,7 мДж)/(27 Дж)» 10–4 = 0,01%.
Ответ: A min» 2,7 мДж; КПД примерно равен 0,01%.
5. Коробку с большим количеством маленьких лампочек накаливания с рабочими параметрами 2 В, 0,5 Вт выбросили за ненадобностью, а Вася подобрал и принес в школу, чтобы с их помощью подключить к сети 220 В электрический паяльник, на корпусе которого написано 40 В, 40 Вт. Помогите Васе придумать электрическую схему включения. Желательно, чтобы все лампочки и паяльник работали в «номинальном» режиме.
Решение. Номинальная сила тока лампочки равна (0,5 Вт)/(2 В) = 0,25 А, номинальная сила тока паяльника (40 Вт/40 В) = 1 А. Для того, чтобы паяльник работал в номинальном режиме, необходимо чтобы на нем падало напряжение 40 В, а остальные 220 В – 40 В = 180 В падали на лампочках. Так как номинальная сила тока лампочки в 4 раза меньше номинальной силы тока паяльника, то последовательно с паяльником нужно подключить 4 одинаковых параллельно соединенных цепочки лампочек. В каждой из этих цепочек должно быть (180 В)/(2 В) = 90 последовательно соединенных лампочек.
|
|
|
Ответ: Надо последовательно с паяльником включить параллельно 4 гирлянды по 90 последовательно соединенных лампочек в каждой.
|
|
|
