 |
Протяженность одного интервала.
|
|
|
|
А = 
,
где Иmax и Иmin – соответственно наибольшее и наименьшее значения износов (табл.1).
А = 
= 0,143 ≈ 0,15 мм.
Протяженность интервала всегда округляют в большую сторону. Интервалы должны быть одинаковыми по величине и прилегать друг к другу без разрывов. Начало первого интервала, или начало рассеивания (сдвиг износов) определяется по формуле
С = И1 – 0,5 А,
где И1 – значение износа в первой точке информации (наименьший износ), мм.
С = 0,05 – 0,5 ∙ 0,15 = -0,025.
Принимаем С = 0, так как отрицательного износа не может быть. При распределении износов чаще всего С = 0, то есть нет сдвига рассеивания.
Число интервалов и их протяженность используются для построения первой строки статистического ряда. Вторая строка этого ряда представляет собой середину каждого интервала. Например, для первого интервала:
= 0,075.
Третья строка показывает частоту, то есть сколько деталей попадает в каждый интервал износов (берут из табл. 1). При этом, если на границе двух интервалов окажется несколько деталей с равным износом, то их поровну распределяют между этими интервалами. Например, в первом интервале (0-0,15 мм) частота m 1 = 2; во втором – m 2 = 3; в третьем m 3 = 6 (четыре детали с износом 0,35 мм и две детали с износом 0,45 мм, а остальные две детали с износом 0,45 переходят в четвертый интервал). Если окажется, что последнее одно или несколько значений износа (точек информации) выходят за пределы последнего интервала, то нужно либо добавить еще один интервал, либо увеличить протяженность интервалов (А).
Значение опытных вероятностей (или частостей) в каждом интервале (четвертая строка статистического ряда) определяют по формуле
Рi = 
,
|
|
|
где m 1 – опытная частота в i -ом интервале.
Р1 = 
= 0,04; Р2= 
= 0,06 и т.д.
Значения накопленных опытных вероятностей или частостей (последняя строка ряда) определяются суммированием вероятностей по интервалам:
Pi = 
ΣР1 = 0,04; ΣР2 = 0,04 + 0,06 = 0,1; ΣР3 = 0,1 + 0,12 = 0,22 и т.д.
или ΣР1 = 0,04; ΣР2 = 
= 0,1 и т.д.
Сумма частот Σ m 1 по всем интервалам должна быть равна N (т.е. 50), а сумма накопленных опытных вероятностей ΣРi = 1,0.
Таблица 2 – Статистический ряд
| Интервал, мм | 0- 0,15 | 0,15-0,30 | 0,30-0,45 | 0,45-0,60 | 0,60-0,75 | 0,75-0,90 | 0,90-1,05 |
| Середина интервала, Иср i Частота Опытная вероятность, Рi Накопленная опытная вероятность, РΣРi | 0,075 0,04 0,04 | 0,225 0,06 0,10 | 0,375 0,12 0,22 | 0,525 0,24 0,46 | 0,675 0,38 0,84 | 0,825 0,12 0,96 | 0,975 0,04 1,00 |
Определение числовых характеристик. Основными числовыми характеристиками распределения случайной величины являются среднее значение, среднее квадратичное отклонение и коэффициент вариации.
Среднее квадратическое отклонение представляет собой абсолютную меру, а коэффициент вариации – относительную меру рассеивания (разброса) случайной величины. При объеме выборки (информации) N ≥ 25 их определяют следующим образом.
Среднее значение износа
= 
Иср i ∙ Рi,
где Иср i - значение износа в середине i -го интервала (середина i -го интервала);
Рi – опытная вероятность в i -ом интервале.
В нашем примере:
= 0,075 ∙ 0,04 + 0,225 ∙ 0,06 + 0,375 ∙ 0,12 + 0,525 ∙ 0,24 + 0,675 ∙ 0,38 +
+ 0,825 ∙ 0,12 + 0,975 ∙ 0,04 = 0,60 мм.
Среднее квадратическое отклонение:
σ = 
В нашем примере:
σ = 
 |
-0,60)2∙0,24+(0,675-0,60)2∙0,38+(0,825-0,60)2∙0,12+(0,975-0,60)2∙0,04=0,20 мм.
Коэффициент вариации:
V = 
= 0,33.
Проверку информации на наличие выпадающих точек осуществляют по формуле
λоп = 
,
где Иi и Иi-1 – смежные точки в сводной ведомости информации (табл. 1).
Для наименьшего значения износа И3 = 0,20; И2 = И1 = 0,05.
|
|
|
λоп =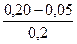 
= 0,75.
Для наибольшего значения износа И50 = 1,05; И49 = 0,95.
λоп = 
= 0,5.
Полученные значения λоп сравнивают с табличными значениями критерия Ирвина (см. прил. 3). Если λоп > λт, то такие точки «выпадают», то есть должны быть исключены из информации как недостоверные. В этом случае необходимо перестроить статистический ряд с учетом уменьшения количества информации за счет выпавших точек, вновь рассчитать , σ и V.
В нашем случае при N = 50 и доверительной вероятности α = 0,95 табличное значение критерия Ирвина λт = 1,1, то есть больше λоп. Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.
Графическое построение опытного распределения износов. Данные табл. 2 используют для построения графиков, наглядно характеризующих опытное распределение случайной величины (в данном случае износов детали): гистограммы 1 и полигона 2 – рис. 1, кривой накопленных (опытных) вероятностей 1 – рис. 2.
При построении опытного распределения износа по оси абсцисс откладывается в произвольно выбранном масштабе значение износа, а по оси ординат – опытная вероятность Рi (рис. 1) или накопленная опытная вероятность 
(рис. 2).
Масштаб ординаты следует выбирать придерживаясь правила «золотого сечения»:
У =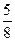 
х,
где У – длина наибольшей ординаты;
х – длина абсциссы, соответствующей наибольшему значению износа.
Построение гистограммы осуществляется следующим образом (рис. 1).
По оси абсцисс откладывают интервалы в соответствии со статистическим рядом, а по оси ординат – опытную вероятность Р в начале и конце каждого интервала. Соединив построенные в каждом интервале точки, получаем прямоугольник. В результате получается ступенчатый многоугольник – гистограмма. Площадь каждого прямоугольника в процентах от общей площади гистограммы или долях единицы определяет опытную вероятность или количество деталей, у которых износ находится в данном интервале.
Построение полигона (рис. 1) осуществляется по точкам, образованным пересечением абсциссы, равной середине интервала, и ординаты, равной опытной вероятности интервала, то есть надо соединить прямыми линиями середины верхних (горизонтальных) сторон прямоугольников гистограммы.
|
|
|
Точки кривой накопленных опытных вероятностей образуются пересечением абсциссы, равной концу данного интервала, и ординаты, равной сумме вероятностей предыдущих интервалов (рис. 2). Гистограмма и полигон являются дифференциальными, а кривая накопленных опытных вероятностей – интегральным статистическим (опытным) законом распределения случайной величины.
|
|
|
