 |
§ 7. 6. Антенна с бегущей волной
|
|
|
|
Из полученного в предыдущем параграфе выражения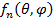 
для множителя дискретной решетки, т. е. решетки, состоящей из отдельных излучателей, расположенных на некотором расстоянии d друг от друга, можно получить выражение для непрерывной линейной системы излучателей. Такой системой является проводник с бегущей волной или длинная щель в волноводе.
Не детализируя реальную излучающую систему, можно представить ее следующим образом: это произвольная излучающая линия (рис. 7. 13), однородная в направлении оси х и возбужденная токами с фазовым распределением, соответствующим бегущей волне с фазовой скоростью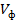 
.
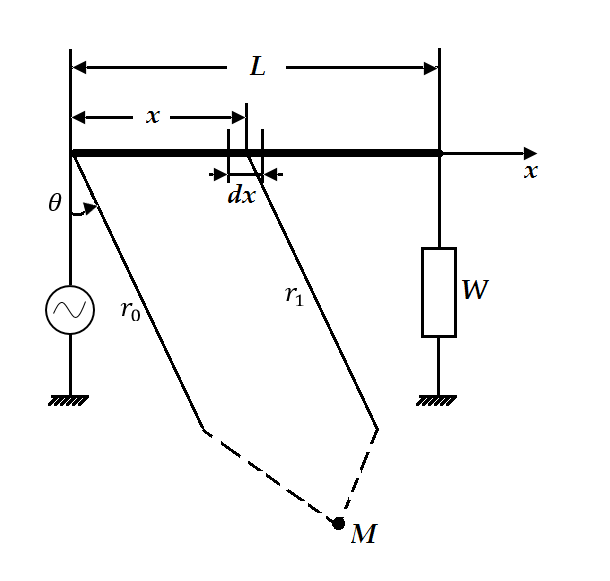
Рис. 7. 13. Провод, обтекаемый бегущей волной тока
Замедление волны в проводе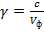 
, что соответствует постоянной распределения 
.
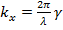Разобьем мысленно излучающую линию (см. рис. 7. 13) на N излучающих частей длиной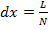 
. Сдвиг фаз между соседними элементами
.
Будем считать, что поле, излученное элементом провода dx, определяется так же, как и для элементарного диполя:
.
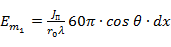Тогда амплитуда результирующего поля
Чтобы получить из (7. 12) выражение для амплитуды поля непрерывной решетки, следует учесть, что последняя получается предельным переходом от дискретной решетки, когда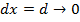 
, а число излучателей 
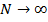. Так как при этом аргумент синусоидальной функции, стоящей в знаменателе выражения (7. 12), мал, а 
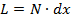, то
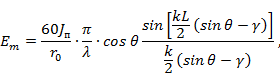
или
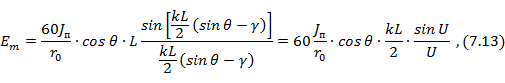
где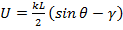 
.
Таким образом, для провода с бегущей волной множитель системы
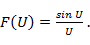
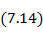
График функции 
показан на рис. 7. 14, а. Эта функция непериодическая и имеет одно наибольше значение, равное единице при U = 0. Из формулы (7. 14) следует, что уровень первого бокового лепестка относительно главного составляет 0, 21 (-13, 5 дБ).
|
|
|
Проанализируем множитель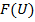 
непрерывной системы, определяющий ее направленные свойства, так как направленность элементар ных источников, образующих непрерывную систему, выражена весьма слабо. На рис. 7. 14. изображены графики функции » на которых штриховкой выделены участки, находящиеся в интервале 
обобщенной координаты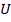 
. Этот интервал изменения 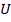соответствует реальной ДН, т. е. значениям угла 
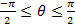. В случае 
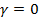(синфазная система) интервалу углов 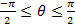соответствует интервал 
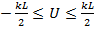(рис. 7. 14, б). Диаграмма направленности, изображенная на этом рисунке, довольно хорошо совпадает с ДН дискретной решетки, если число излучателей в ней 
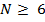(при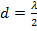 
).
Рис. 7. 14. К анализу множителя непрерывной системы излучателей:
а-вид функции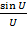 
;
б-е-графики функции 
при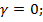 
Для определения ширины ДН по уровню 0, 7 поля необходимо положить 
, т. е. решить трансцендентное уравнение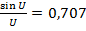 
. Из решения этого уравнения следует 
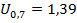, откуда 
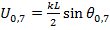и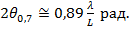 
Если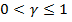 
, что соответствует линейному изменению фазы вдоль провода, интервал изменений 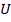сдвигается влево по оси (рис. 7. 14, в, г). Главный максимум ДН наклоняется при этой к оси решетки по направлению распространения волны ( 
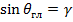), и при 
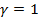он ориентирован вдоль оси системы. При 
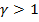весь интервал изменения обобщенной координаты 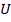, для которого 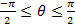, расположен в пределах отрицательных значений оси 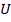. Если 
незначительно превышает единицу, то главный максимум ориентирован в направлении оси провода, но его величина уменьшается (рис, 7. 14, д). С увеличением замедления величина главного максимума может сравняться с величиной первого бокового лепестка, и ДН провода будет состоять из нескольких примерно одинаковых лепестков (рис. 7. 14, е).
Ширина ДН отклоненного луча при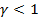 
может быть определена по формуле
|
|
|
где 
—эффективная длина раскрыва системы.
Эта формула справедлива во всем секторе углов, кроме сектора, примыкающего к оси решетки и равного одной ширине главного лепестка ДН. В этом секторе не существует точки, соответствующей уровню 0, 7 поля с одной стороны главного лепестка ДН [12].
При излучении точно в направлении оси провода, имеющего большую длину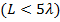 
, ширина ДН
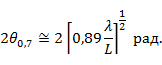
Таким образом, при осевом излучении зависимость ширины ДН от относительной длины антенны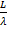 
более слабая, чем в случае синфазной антенны или антенны с линейным изменением фазового сдвига[2].
Следовательно, при отклонении ДН, т. е. при сканировании, ширина ДН изменяется; изменяется также ширина и форма боковых лепестков. Если при 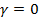главный лепесток ДН имеет форму диска (рис. 7. 15, а), а при 
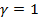- вытянутого эллипсоида вращения (рис. 7. 15, в), то при 
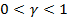направления главного излучения образуют поверхность конуса вращения относительно оси системы (рис. 7. 15, б).
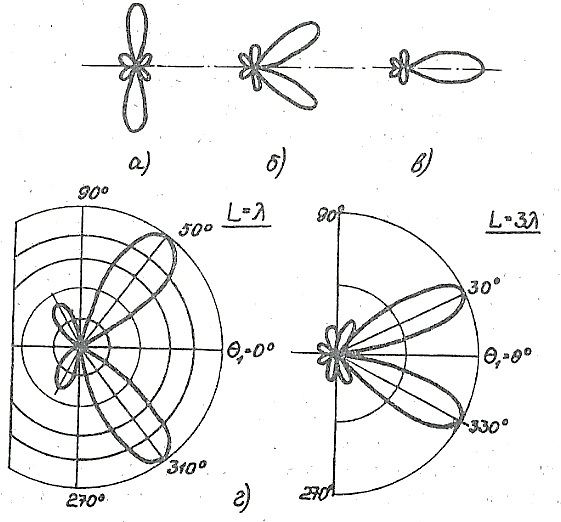
Рис. 7. 15. Изменение формы ДН антенны бегущей волны
при отклонении главного максимума:
а-поперечное излучение; б-наклонное излучение;
в-продольное излучение;
г-зависимость направления максимального излучения антенны бегущей волны от ее длины
Если 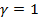, а элементарные источники, образующие провод с бегущей водной, обладают направленными свойствами 
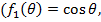формула (7. 13)), то в направлении оси провода ( 
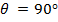), где множитель системы 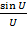максимален, результирующее поле обращается в нуль, так как в выражении (7. 13) 
. В связи с этим результирующее поле оказывается максимальным в некотором промежуточном направлении, составляющем угол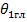 
с осью провода. При большой относительной длине провода ( 
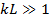) это направление можно приближенно определить с использованием формулы (7. 13) путем приравнивания числителя значению 
:
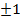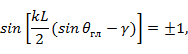
откуда
.
Если принять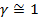 
и ввести в рассмотрение угол 
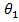, отсчитываемый от оси провода ( 
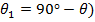, то
При большой длине провода угол 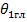мал, и 
можно разложить в ряд
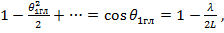откуда 
Так, если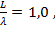 
то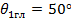 
, а если если 
то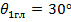 
(рис. 7. 15, г).
Изменение длины волны генератора слабо сказывается на направлении максимального излучения 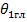, а также на входном сопротивлении. Поэтому провод в режиме бегущей волны является диапазонной антенной.
Следует учитывать тот факт, что реальные антенны бегущей волны имеют не постоянное, а спадающее от начала к концу амплитудное распределение поля (тока) вследствие наличия затухания, обусловленного излучением энергии. Это вызывает изменение формы ДН провода. Однако, если поле в конце провода уменьшается не более чем в три раза по сравнению с полем в начале, искажения ДН незначительны и при расчете ДН можно пользоваться множителем системы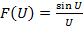 
.
|
|
|
|
|
|
