 |
§ 7. 2. Общий метод расчета диаграмм направленности антенных решеток
|
|
|
|
§ 7. 2. ОБЩИЙ МЕТОД РАСЧЕТА ДИАГРАММ НАПРАВЛЕННОСТИ АНТЕННЫХ РЕШЕТОК
Рассмотрим общий метод расчета ДН антенных решеток, при этом наиболее подробно остановимся на расчете ДН для антенных систем, состоящих из полуволновых вибраторов.
Поле излучения антенной решетки представляет собой результат интерференции полей отдельных излучателей. Поэтому надо найти отдельно поле от каждого излучателя в данной точке пространства, а затем суму полей всех излучателей при учете амплитудных и фазовых соотношений.
Расчет диаграммы направленности таких антенн целесообразно производить в следующем порядке:
1. Определить амплитудную и фазовую диаграмму излучения отдельных элементов, составляющих антенную решетку.
2. Найти фазовый центр каждого излучателя и заменить излучатели воображаемыми точечными излучателями, расположив последние в фазовых центрах реальных излучателей. Каждому точечному излучателю приписать равномерную фазовую диаграмму и амплитудную диаграмму реального излучателя. Тогда точечный излучатель в отношении внешнего действия будет полностью эквивалентен реальному излучателю.
3. Вычислить амплитуды и фазы полей, создаваемые эквивалентными излучателями в произвольной точке пространства (каждым в отдельности). При этом рассматривать поле на большом (по сравнению с размерами антенны и длиной волны) расстоянии от антенны. В процессе вычисления амплитуд полагать расстояния от точки наблюдения до всех излучателей одинаковым и равным расстоянию до какого-либо излучателя. Расчет фаз следует, однако, вести с учетом разницы в расстояниях до каждого излучателя. При определении разницы в расстояниях в целях упрощения следует считать направления на точку наблюдения параллельными для всех излучателей. При вычислении фаз надо определить фазы по отношению к фазе поля какого-либо одного излучателя, принимаемой за начальную.
|
|
|
4. Определить амплитуду и фазу поля всей антенны путем суммирования полей всех составляющих ее излучателей, учитывая амплитудные и фазовые соотношения, а также поляризацию полей.
§ 7. 3. ИЗЛУЧЕНИЕ ЛИНЕЙНОЙ СИНФАЗНОЙ АНТЕННЫ
При расчете поля излучения синфазной антенны с равномерным амплитудным распределением приходится иметь дело со сложением некоторого числа одинаково поляризованных гармонических колебаний с равными амплитудами и фазами, отличающимися друг от друга на одинаковый угол.
Сумму N таких колебаний проще всего получить геометрическим путем. Пусть имеется ряд таких колебаний:
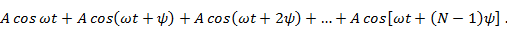
Представим каждое слагаемое вектором, имеющим модуль, равный амплитуде поля излучения А, и расположенным соответственно фазе колебания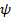 
. При суммировании векторов образуется правильный многоугольник (рис. 7. 5). Опишем вокруг него окружность радиуса 
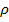с центром в точке o. Тогда 
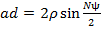, так как 
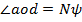. Из 
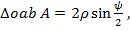откуда 
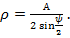Таким образом, амплитуда результирующего колебания
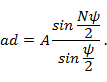
Фаза результирующего колебания по отношению к фазе начального колебания определяется величиной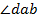 
и равна 
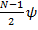. Сумма всех колебаний
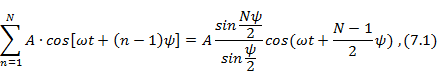
где 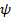- разность фаз между соседними колебаниями. Фаза результирующего колебания опережает фазу исходного на угол .
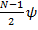На практике получили распространение антенные решетки, составленные из вертикальных или горизонтальных полуволновых вибраторов (рис. 7. 6, а, б).
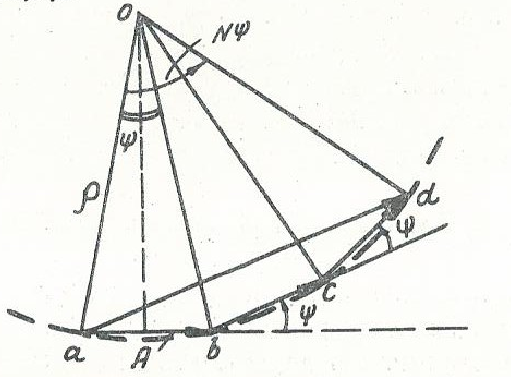
Рис. 7. 5. Векторная диаграмма суммирования полей вибраторов
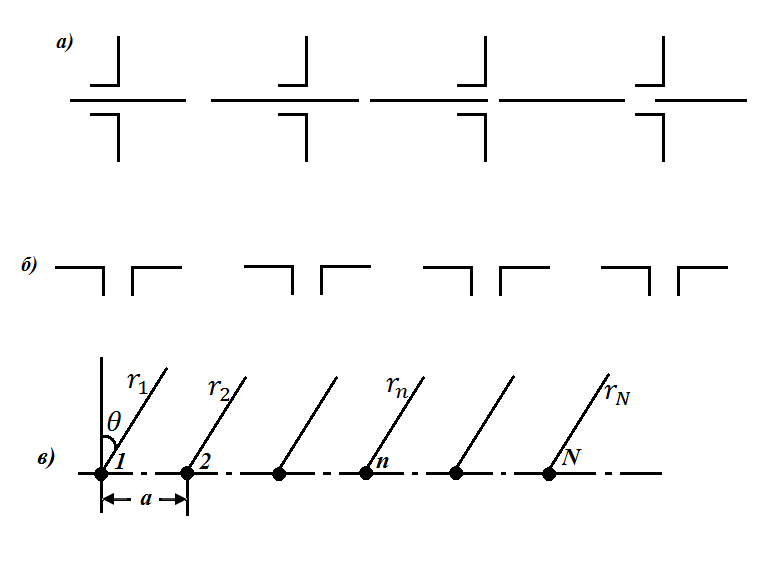
Рис. 7. 6. Линейные решетки излучателей:
а - из вертикальных вибраторов; б - из горизонтальных
вибраторов; в - к расчету ДН линейной синфазной решетки
Такие антенны состоят из N синфазно питаемых полуволновых вибраторов, одинаково ориентированных и расположенных на одинаковом расстоянии друг от друга. Направление расположения образует прямую линию.
|
|
|
Для расчета диаграммы направленности заменим каждый вибратор эквивалентным точечным излучателем, расположив его в фазовом центре, т. е. в середине вибратора. Тогда, независимо от того, горизонтальные или вертикальные вибраторы в решетке, схема примет вид, показанный на рис. 7. 6, в. Поле такой антенны - результат интерференции полей вибратор. Так как вибраторы параллельны, то поля одинаково поляризованы, а следовательно, можно пользоваться полученной выше формулой для суммарного поля. Рассматривая поле далеко от антенны, т. е. на расстоянии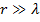 
, можно считать, что (см. рис. 7. 6, в) 
.
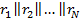Пусть мгновенное значение тока в пучности каждого вибратора описывается уравнением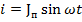 
. Тогда суммарное поле в точке наблюдения от всей антенны будет
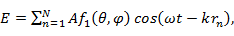
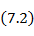
где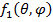 
- диаграмма направленности эквивалентного излучателя (она совпадает с диаграммой отдельного вибратора);
А - постоянный (амплитудный) множитель, не зависящий от углов
;
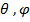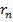- расстояние от n-го излучателя до точки наблюдения.
Примем фазу поля от наиболее удаленного излучателя (у нас - 1-го) за начальную. Тогда для определения фазы поля n - го излучателя необходимо предварительно выразить расстояние от этого излучателя до точки наблюдения через расстояние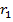 
. Из рис. 7. 6, в видно, что
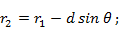
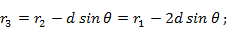
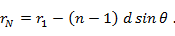
Подставляя значение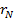 
в формулу (7. 2) для напряженности поля, получаем
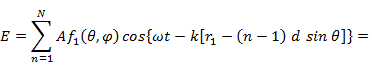
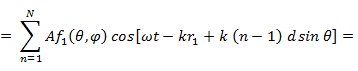
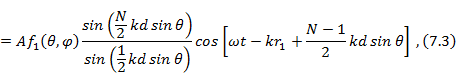
где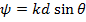 
- разность фаз между полями соседних излучателей;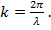 
Проведем анализ полученного выражения. Амплитудная диаграмма направленности согласно формуле (7. 3)
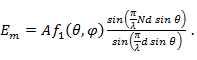
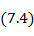
Она представляет собой произведение диаграммы составляющего излучателя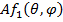 
на множитель антенны:
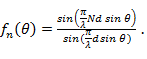
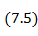
Из формулы (7. 3) следует, что фаза поля изменяется при изменении угла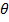 
. Таким образом, при отсчете расстояния от наиболее удаленного излучателя синфазная антенна не имеет равномерной фазовой диаграммы, а выбранная точка начала отсчета расстояний не является фазовым центром.
|
|
|
Фазовой диаграммой будем называть в дальнейшем ту часть выражения, определяющего фазу поля, которая не зависит от времени (см. формулу (7. 3)):
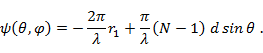
Выясним, имеет ли рассматриваемая антенна фазовый центр и где он находится. Предположим, что фазовый центр имеется и находится на линии расположения излучателей на расстоянии х от 1-го излучателя. Обозначим расстояние от фазового центра до точки наблюдения через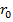 
и выразим расстояние 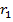через :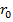
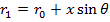. Тогда
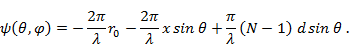
Если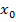 
- координата фазового центра, то это выражение при 
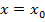не должно зависеть от 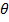. Требуя выполнение этого условия, получаем 
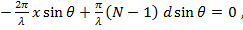откуда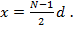 
Таким образом, рассматриваемая антенна имеет фазовый центр, который совпадает с ее геометрическим центром. Этот вывод справедлив в общем случае для любой синфазной антенны.
При отсчете расстояния от фазового центра с учетом того, что амплитуда поля практически не меняется при перемене начала отсчета в пределах антенны, поле антенны
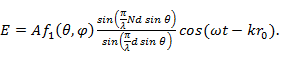
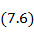
Так как вибраторы, образующие решетку, обладают слабой направленностью, то ДН решетки в основном определяется множителем решетки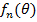 
. Множитель решетки зависит от числа излучателей и расстояния между ними, выраженного в длинах волн 
(см. Формулу (7. 5)). Этот множитель не зависит от угла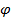 
, а это значит, что в плоскости, перпендикулярной линии расположения излучателей (пл. 
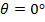), ДН решетки совпадает с диаграммой одиночного излучателя, а поле возрастает пропорционально их числу:
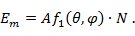
Это следует из выражения (7. 4) при значении .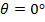
В плоскости, проходящей через линию расположения излучателей (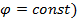 
, ДН решетки отличается от диаграммы одиночного излучателя. Пусть в этой плоскости ДН одиночного излучателя ненаправленная. Тогда ДН решетки будет определяться только множителем решетки, который в нормированном виде
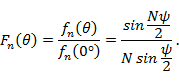
Множитель решетки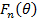 
является периодической функцией с периодом 2π и при изменении угла 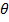проходит через свои максимальные и минимальные значения. Поэтому ДН решетки имеет многолепестковый характер (рис. 7. 7). В каждом из периодов этой функции имеется один главный лепесток и несколько боковых. График функции Fn(θ ) симметричен относительно точек 
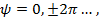а сама функция при этих значениях 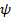максимальна.
|
|
|
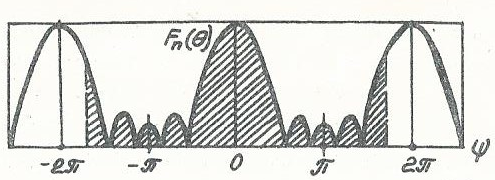
Рис. 7. 7. График функции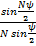 
(заштрихована та ее часть, которая соответствует
реальной ДН,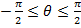 
)
Между соседними главными лепестками имеется N-1 направлений нулевого излучения и N-2 боковых лепестков, максимумы которых убывают при удалении от каждого главного лепестка. Наименьшими при этом являются те лепестки ДН, которые находятся в середине интервала между соседними главными максимумами. Относительная величина боковых лепестков
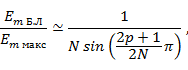
где р = 1, 2, 3…
В решетках с большим числом излучателей уровень первых боковых лепестков может быть найден по упрощенной формуле (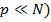 
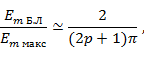
и при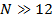 
первый боковой лепесток составляет величину, равную 0, 217 (или -13, 5 дБ) относительно главного.
На практике обычно требуется получить ДН решетки с одним главным максимумом излучения. Для этого необходимо, чтобы в интервал изменения обобщенной координаты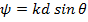 
, определяемый неравенством 
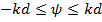и соответствующий реальной ДН решетки ( 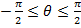), попадал лишь один главный максимум функции 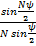(см. рис. 7. 7). Это будет в том случае, если ширина интервала изменения 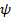, равная 2kd, меньше 4π , т. е. 2kd < 4π или d < λ . Таким образом, расстояние между соседними излучателями в решетке должно быть меньше длины волны генератора.
Угловые границы главного лепестка по уровню нулевого излучения могут быть найдены из формулы (7. 6) путем приравнивая нулю числителя множителя решетки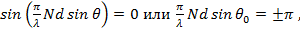 
так как множитель решетки с изменением угла 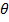изменяется значительно быстрее, чем первый множитель формулы (7. 6), и определяет в основном ДН решетки. Из последнего соотношения следует 
.
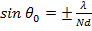При большом числе излучателей (N > 4) можно принять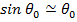 
. Отсюда угловая ширина главного лепестка ДН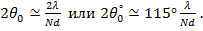 
Таким образом, для получения узких ДН необходимо увеличивать длину антенны Nd. Но так как расстояние между излучателями должно быть меньше длины волны генератора (для получения одного главного максимума излучения), повышения направленности добиваются увеличением числа излучателей решетки N.
Ширину ДН по уровню 0, 7 поля можно определить по приближенной формуле
Формула (7. 7) тем точнее, чем больше число вибраторов в решетке при заданной величине отношения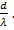 
Практически ею можно пользоваться, если
.
Если излучатели, образующие линейную синфазную антенну, обладают направленными свойствами в плоскости, проходящей через линию их расположения (рис. 7. 8), то расстояние между излучателями можно взять больше длины волны генератора (d > λ ). В этом случае в интервале изменения обобщенной координаты 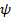, соответствующем реальной ДН решетки, может оказаться несколько максимумов функции 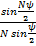. В результирующей ДН они будут отсутствовать, если в этих направлениях ДН одиночного элемента решетки имеет нулевое или почти нулевое значение. Таким образом, выбором соответствующего расстояния между излучателями (при d > λ ) можно получить результирующее излучение с относительно низким уровнем боковых лепестков.
|
|
|
Если расстояние между излучателями выбрано таким, что можно пренебречь влиянием их полей друг на друга, то к. н. д. решетки можно подсчитать по приближенной формул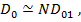е 
где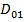 
- коэффициент направленного действия одиночного излучателя в свободном пространстве.
Рассмотренные линейные решетки обладают направленностью только в одной плоскости - в плоскости расположения излучателей.
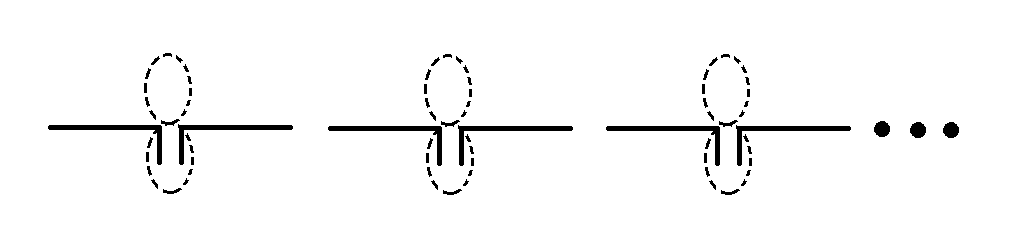
Рис. 7. 8. Линейная решетка направленных излучателей
|
|
|
