Определение необходимого числа испытаний

При проведении тех или других испытаний необходимо знать, достаточно ил проведено испытаний или их необходимо увеличить. Для решения поставленной задачи необходимо знать относительную ошибку и доверительную вероятность, а также задаться коэффициентом вариации.

Абсолютная доверительная ошибка, допущенная при определении среднего значения генеральной совокупности для нормального распределения в симметричном доверительном интервале, определяется по формуле:

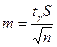, (41)

тогда относительная доверительная ошибка среднего значения:

 

, (42)

 

т.к. , то , (43)

Если принять, что γ =0,95, то t~2, тогда:

 

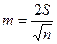и .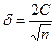

 

Исходя из формулы (43) можно рассчитать доверительный объем измерений при определении выборочного среднего значения:

 

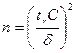, (44)

 

Для определения общей гарантийной ошибки используется формула:

, (45)

 

При измерениях возникают ошибки двоякого рода:

- ошибки измерения (А_m);

- ошибки, вызванные неравномерностью самого материала m.

В приведенных выше формулах предполагалось, что абсолютные погрешности измерений равны нулю. Однако практически измерения выполняются с какой-то погрешностью, которая обычно нам не известна. Если принять самый неблагоприятный случай, когда все измерения получены с односторонней предельной ошибкой, т.е. при +А_m и –А_m, тогда совместный учет предельных абсолютных погрешностей и ошибки выборки будет:

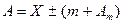, (46)

Предположим, что ошибки отдельных измерений подчиняются нормальному распределению, а величина R соответствует максимальному размаху, обусловленному нормальной погрешностью измерений:

 

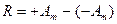, (47)

 

При таких условиях среднее квадратическое отклонение вследствие погрешности измерений будет определяться по формуле:

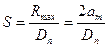, (48)

 

где D_n – коэффициент, зависящий от числа испытаний (таблица 7).

Таблица 7.

 

N
Dn	3,17	3,68	3,98	4,20	4,79	5,20	6,00

 

Учитывая, что дисперсия измерений не зависит от дисперсии неравномерности материала, и применяя правило сложения дисперсий, можно определить общую ошибку по формуле, в которой учтены ошибка выборки и абсолютная погрешность измерения:

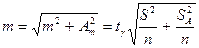, (49)

где m – ошибка выборки при выбранной доверительной вероятности; А_m – случайная ошибка измерения; t_γ – квантиль распределения Стьюдента; S_А – дисперсия для оценки А (дисперсия неравномерности объекта измерения).

 

Сравнение результатов измерений. Сравнение двух средних независимых выборок

Часто в процессе проведения испытаний необходимо сравнить результаты двух независимых выборок с тем, чтобы оценить достоверность разности 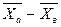. Если эта разность недостаточно значима, то средние 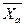и 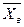могут относиться к одной и той же генеральной совокупности. Если же эта разность достаточно значима, то средние 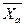и 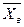относятся к разным генеральным совокупностям или к одной совокупности, но при измерении величин 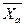и 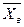имеется достаточная разница в методах их определения.

При большом числе испытаний n>30 и m>30 критерий достоверности определяется по формуле:

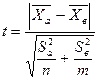, (50)

 

Полученное значение сравнивают с табличными значениями критерия Стьюдента.

При малом числе испытаний n+m<60:

 

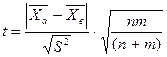, (51)

 

При пользовании формулой (51) находят значение 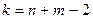и по таблице 8 для найденной величины k при вероятности 95% определяют табличное значение t.

Таблица 8.

 

k	t	k	t	k	t	k	t
	12,78		2,23		2,09		2,05
	4,30		2,20		2,09		2,05
	3,18		2,18		2,08		2,04
	2,78		2,16		2,07		2,02
	2,57		2,14		2,07		2,00
	2,45		2,13		2,06		1,98
	2,37		2,12		2,06	∞	1,96
	2,30		2,11		2,06	-	-
	2,26		2,10		2,05	-	-

 

Если t_p>t то разность средних 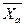и 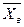при нормальном распределении достоверна более чем на 95%. Если t_p<t, то разность средних не считается достаточно достоверной.

 

Оценка соответствия фактического распределения результатов испытаний нормальному закону

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: