 |
Функция как закон соответствия между множествами
|
|
|
|
Пусть задано числовое множество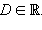 
Если каждому числу 
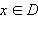поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция:
y = f (x),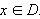 
|
Множество D называется областью определения функции и обозначается D (f (x)). Множество, состоящее из всех элементов f (x), где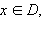 
называется областью значений функции и обозначается E (f (x)).
Число x часто называют аргументом функции или независимой переменной, а число y – зависимой переменной или, собственно, функцией переменной x.
Функции f и g называются равными, если они имеют одну и ту же область определения D и для каждого 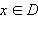значения этих функций совпадают. В этом случае пишут f (x) = g (x), 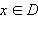или f = g.
Функция, в которой каждому элементу множества А соответствует не более 1 элемента множества В называется однозначной (в обратном случае – неоднозначной). Если функция однозначна и всюду определена, то это отображение множества А на множество В.
Функция внутрь множества В – область значений не совпадает со всем множеством В. Функция на всё множество В – всё элементы множества захвачены. Если каждому элементу множества В соответствует 1 и только 1элемент из множества А, то такая функция Инъективна.
Класс элементарных функций
Элементарные функции — функции, которые можно получить из основных элементарных функций (полиномиальная функция, рациональная, степенная, показательная и логарифмическая, тригонометрические и обратные тригонометрические) с помощью конечного числа арифметических действий и композиций. Каждую элементарную функцию можно задать формулой, т.е. набором конечного числа символов, отвечающих перечисленным операциям.
Другими словами,
|
|
|
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
многочлен,
рациональная,
степенная,
показательная и логарифмическая,
тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения. Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
Элементарные функции разделяются на алгебраические и трансцендентные.
Суперпозиция функций.
В математике компози́ция фу́нкций (суперпози́ция фу́нкций) — это применение одной функции к результату другой.
Пусть имеются две функции: z = h (y) и y = g (x), причем область значений функции g принадлежит области определения функции h. Тогда функция z = h (g (x)) называется композицией функций h и g, или сложной функцией, или суперпозицией функций. Аналогично можно рассматривать композицию любого конечного числа функций.
Пример
Функции у = 5sin2(3 x – 1); y = 5sin3 x ; y = x 3 x ; y = ln(ctg x) – композиции различных элементарных функций.
В математическом анализе и теории вероятностей композицией (свёрткой) называют и другие способы образования из двух функций, f (x) и g (x), третьей, h (x), например:
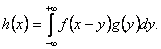
Композицией двух преобразований называют последовательное выполнение этих преобразований, а также полученное в результате этого итоговое преобразование. Если в результате первого преобразования фигура Ф 1 перешла в фигуру Ф 2, а в результате второго преобразования фигура Ф 2 перешла в фигуру Ф 3, то композиция этих преобразований – преобразование, которое переводит фигуру Ф 1 в фигуру Ф 3.
|
|
|
Вообще термин «композиция» употребляют для обозначения любой операции, которая по определенному правилу ставит в соответствие паре элементов третий элемент.
Происхождение термина – латинское слово composition (составление).
|
|
|
