 |
Замечательный» предел - предел отношения синуса бесконечно малого угла к этому углу.
|
|
|
|
. 
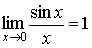
Для доказательства первого предела используется неравенство
 ,
|
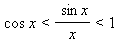верное для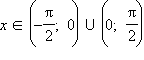 
(неравенство sin x < x следует из определения синуса при рассмотрении единичной окружности, а для доказательства неравенства x < tg x необходимо нарисовать ось тангенсов). Для доказательства второго предела используется монотонная и ограниченная последовательность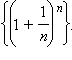 
Определение непрерывности функции в точке.
Функция f(x) называется непрерывной справа в точке xo, если предел
,
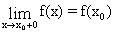и непрерывной слева в точке xo, если предел
.
Непрерывность функции в точке xo равносильна ее непрерывности в этой точке одновременно и справа и слева.
Для того, чтобы функция была непрерывна в точке xo, например, справа, необходимо, во-первых, чтобы существовал конечный предел 
, а во-вторых, чтобы этот предел был равен f(xo). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.
35.Непрерывность функции на отрезке.
Функцию y = f(x) называют непрерывной на отрезке [ a, b ], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.
Свойства функций, непрерывных на отрезке
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О[a, b]
|
|
|
Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0. (теорема Больцана-Коши).
Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX.
Теорема 4. Если функция непрерывная на отрезке,принимает в какой-то точке этого отрезка положительные(отрицательные) значения,то имеется некоторая окрестность этой точки,во всех точках которой функция тоже положительна(отрицательна).
Производная функции
Определение производной.
Производной функции f(x) в точке x0 называется предел отношения приращения функции Δ f в этой точке к приращению аргумента Δх, когда последнее стремится к нулю (бесконечно малому).
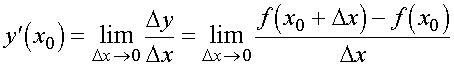
Приращение функции и вычисление средней скорости изменения функции.
Одним из основных свойств, характеризующих функцию, является скорость ее изменения. Пусть аргумент х функции f(x) получил приращение Δх, т.е. начальное значение аргумента равно х, а конечное х+Δх. Вычислим приращение функции, обусловленное приращением аргумента:
Δ f(х) = f(x + Δ х) - f(x) (1)
Приращение функции или аргумента – алгебраическая величина, которую нельзя отождествлять с «увеличением». Действительно, если f(x+Δх)<f(x), то Δf(x)<0 и приращение нашей функции отрицательно.
Средняя скорость изменения функции на участке от х до х+Δх, вычисляется по формуле:
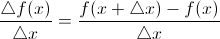(2)
Замечание: Средняя скорость изменения, как характеристика функции обладает существенным недостатком, проилюстрируем этот недостаток на примере. Пусть функции f1(x) и f2(x) получили одинаковые приращения при изменении аргумента от х до х+Δх, следовательно, одинаковыми будут и средние скорости изменения функций f1 и f2 на этом отрезке. Между тем, на практике может быть, что функция f2(х) меняется гораздо быстрее, резче, чем f1 (х).
|
|
|
|
|
|
