Последовательность - функция натурального аргумента.

 

1. Последовательностью называется бесконечное занумерованное множество действительных чисел, обозначаемое а₁, а₂,..., а_n,..., или кратко

Другое определение последовательности — функция натурального аргумента.

 

Бесконечно малые последовательности

 

Последовательность {α _n } называется бесконечно малой, если

Оределение. Последовательность { x_n } называется бесконечно малой, если , то есть если .

Бесконечно малые последовательности имеют следующие свойства.

1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность.

2. Бесконечно малая последовательность ограничена.

3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.

4. Если { x_n } – бесконечно большая последовательность, то, начиная с некоторого N, определена последовательность {1/ x_n }, и она есть бесконечно малая последовательность. Наоборот, если { x_n } – бесконечно малая последовательность и все x_n отличны от нуля, то {1/ x_n } есть бесконечно большая последовательность.

 

Билет. «»

Последовательность a_n называется бесконечно малой, если для любого сколь угодно малого положительного числа () обязательно найдется такой номер, зависящий от выбранного числа ()который обладает свойствами:

( _E > 0₎ для любого последующего номера будет выполняться условие: все элементы по модулю в дальнейшем будут меньше

> 0 N → ( _n > N _, |a_n| <

Билет. «»

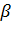Свойства ( _{n, n n)}

Сумма двух БМП, если БМП

C_n = a_n + b_n /последователно складываются почленно/

Произведение последовательностей на постоянную величину.

C * a_n = {c * a_n}

Алгебраическая сумма двух БМП, есть БМП.

Алгебраическая сумма конечного числа бесконечно малой последовательности, есть бесконечно малая последовательность.

Произведение БМП на ограниченную последовательность, есть БМП.

Следствия:

Произведение двух БМП, есть БМП.

Произведение конечного числа БМП, есть БМП.

Билет 13. «Бесконечно большие последовательности»

Если для любого сколь угодно большого положительного числа E, обязательно существует такое N, что для любого следующего числа после N выполняется условие |a_n > E|

> 0 N → ( _n > N _, |a_n| <

 

Билет «»

Из определений бесконечно большой и бесконечно малой последовательностей, следует, что если a_n – бесконечно большая последовательность, то 1 бесконечно малая, а если a_n – бесконечно малая последовательность, то – бесконечно большая.

Билет. «»

Число 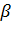называется пределом функции f(x) в точке x = a, если для любой последовательности x_n,, сходящейся к a x_n D(f), x_n a при значении функции y = f(x_n) сходится и ее предел равен .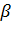

 

 

Вопрос.

 

Число a называется пределом последовательности { x_n }, если для каждого ε > 0 существует такой номер N _ε, что для всех n ≥ N _ε выполняется неравенство | x_n – a | < ε

т. е. 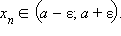При этом пишут, что или 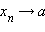при n → ∞. Кратко это определение можно записать так:

 

Вопрос.

Предел суммы равен сумме пределов:

Предел разности равен разности пределов:

Предел произведения равен произведению пределов:

Предел частного равен частному пределов.

 

Имеют место следующие арифметические свойства пределов вещественных последовательностей:

, где k — константа;

, если указанные пределы существуют;

при том же условии;

, если пределы существуют и .

 

Вопрос

Число a – предел последовательности x_n, если в любую окрестность числа а, начиная с некоторого номера попадают все члены последовательности .

 

Пример:

Показать, что последовательность не имеет предела. Действительно, пусть а – предел x_n..

Выберем интервал с длиной . Расстояние между -1 и 1 равно 2 и, следовательно, они оба не могут попадать в этот интервал.

 

Вопрос

Теорема о единственности предела последовательности

Докажем следующую теорему.

Теорема 1. Любая сходящаяся последовательность имеет единственный предел.

Доказательство. Предположим, что это не так, т. е. xna и xnb одновременно. Выберем числа 1 и 2 таким образом, чтобы множества, задаваемые неравенствами , не пересекались. По определению предела последовательности, начиная с некоторых значений N1 (N2), все члены последовательности принадлежат первому (второму) из этих множеств. Выберем в качестве N3=max(N1, N2). Тогда, начиная с номера N3, все члены последовательности принадлежат обоим этим множествам, что невозможно.

 

21 Билет. Теоремы об арифметических свойствах пределов последовательности:

теорема1. Если последовательности {x_n} и {y_n} сходятся,то сходиться последовательность {x_n+y_n} и справедлива формула:

краткая формульровка этой теоремы: преде суммы равен сумме пределов, если пределы {x_n} _и {y_n} существуют и конечны.

Теорема2. Предел производной равен произведению пределов:

, если пределы {x_n} и {Y_n} существуют и конечны.

Теорема3. Постоянную велечину можно выносить за знак предела:

Lim(с* a_n)= c* lim a_n

Теорема4. Предел отношения равен обношению пределов:

. если пределы {X_n} и {Y_n} существуют и конечны.()

доказательство:

докажем теорему1: пусть , а lim y_n=y

 

(n стремиться к бесконечн). Возьмем произвольное число E(эпсюл)>о. Тогда существуют числа N₁ и N₂ такие, что при всех n>N₁ |x_n-x|> E/2,

при всех n>N_{2 |}y_n-y|<E/2.

Пусть N₃- число больше,чем N₁ и N₂.Тогда при n>N₃ последние два неравенства истинны одновременно. Поэтому: |(x_n+y_n)-(x+y)|=|(x_n-x)+(y_n-y)|</=|x_n-x|+|y_n-y|<E/2+E/2=E

Следовательно последовательность x_n+y_n сходиться и

Остальные правила доказываются аналогично.

⇐ Предыдущая1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: