 |
Основы теории обработки результатов.
|
|
|
|
Министерство Образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ
Им. К.Г.РАЗУМОВСКОГО
(Первый Казачий Университет)
Кафедра физики
Лабораторный практикум по дисциплине физика
Москва 2015
Введение.
Лабораторный практикум по физике предназначен для закрепления теоретических знаний, полученных на лекциях. При выполнении лабораторных работ студент имеет возможность проверить правильность основных законов по всем разделам физики.
Практикум предназначен для студентов всех форм обучения, всех факультетов. Количество и тематика лабораторных работ устанавливается кафедрой с учетом планов изучения физики для различных специальностей.
Общие правила выполнения и оформления лабораторных работ.
Подготовка к выполнению лабораторной работы должна быть сделана до начала занятий в лаборатории. Во время подготовки необходимо уяснить следующее:
~ какой закон изучается в данной работе? Физический смысл измеряемой величины, в каких единицах она измеряется.
~ каким методом проводятся измерения?
~ как механически определяется измерение каждой операции в данной работе?
~ студент должен получить у лаборанта бланки протокола и ознакомиться с установкой.
~ перед началом работы студент опрашивается преподавателем по теории данной лабораторной работы.
~ после выполнения работы оформленный протокол измерений и подсчета конечной (искомой) величины должен быть проверен преподавателем, подписан им и отмечен в журнале отчета.
|
|
|
~ для получения окончательного зачета по данной работе студент обязан ответить на все теоретические вопросы по данной работе.
В лабораторном практикуме приведены основы теории обработки результатов измерений.
Основы теории обработки результатов.
В 1960 г. XI генеральная конференция по мерам и весам приняла систему единиц физических величин, которая названа «Международная система единиц» (французское название «System International» или сокращение по-русски «СИ»). Принятием государственного стандарта ГОСТ 8.417–81. Международная система единиц введена как обязательная при изучении всех дисциплин.
Все единицы, входящие в СИ подразделяются на две категории: основные и производные. Основные единицы независимы друг от друга, а производные устанавливаются с помощью уравнений, связывающих физические величины друг с другом.
Основные единицы приведены в таблице 1. Следует обратить внимание на единицы, получившие название в честь выдающихся ученых – физиков. Наименование единиц (как основных, так и производных) пишется со строчной буквы, а обозначение – с прописных.
Таблица №1.
| Физическая величина | Единица СИ | |
| Наименование | Обозначение | |
| Длина | Метр | м |
| Масса | Килограмм | кг |
| Время | Секунда | с |
| Сила электрического тока | Ампер | А |
| Термодинамическая температура | Кельвин | К |
| Количество вещества | Моль | Моль |
| Сила света | Кандела | кд |
Определение основных единиц физических величин, а также наименование и обозначение производных единиц даны в соответствующих разделах курса физики.
Наряду с основными и производными единицами в системе СИ введены следующие две дополнительные единицы:
- радиан – единица, равная углу между двумя радиусами окружности, длина дуги между которыми равна радиусу;
- стерадиан – единица, равная телесному углу (вершина в центре сферы), вырезающему из поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.
|
|
|
В соответствии с рекомендациями международного комитета мер и весов дополнительные единицы интерпретируются как производные единицы.
Для удобства записи данных вводятся десятичные кратные и дольные единицы физических величин. С этой целью предусмотрен (табл. 2) ряд множителей, равных  (здесь «к» – целое положительное или отрицательное число), и приставок к наименованиям и обозначениям единиц.
(здесь «к» – целое положительное или отрицательное число), и приставок к наименованиям и обозначениям единиц.
Таблица №2.
| Множитель | Приставка | Множитель | Приставка | ||
| наименование | обозначение | наименование | обозначение | ||
 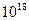
| экса | Э | 
| деци | д |

| пета | П | 
| санти | с |

| тера | Т | 
| милли | м |

| гига | Г | 
| микро | мк |

| мега | М | 
| нано | н |

| кило | к | 
| пико | п |

| дека | д | 
| фемто | ф |
Погрешности измерения.
Измерения физических величин принципиально не могут быть идеально точными, каждый результат измерения отягчен погрешностями.
Погрешностью измерения:
 (1)
(1)
называется отклонение  результата изменения
результата изменения 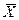 от истинного значения
от истинного значения  измеряемой величины.
измеряемой величины.
В уравнении (1) погрешность  выражена в тех же единицах, что и измеряемая величина
выражена в тех же единицах, что и измеряемая величина  . Такая погрешность называется абсолютной. Чаще оказывается удобней пользоваться относительной погрешностью, представляющей собой отношение абсолютной погрешности измерений к измеряемой величине:
. Такая погрешность называется абсолютной. Чаще оказывается удобней пользоваться относительной погрешностью, представляющей собой отношение абсолютной погрешности измерений к измеряемой величине:
 (2)
(2)
Погрешности классифицируются по свойствам и причинам возникновения.
По свойствам различаются погрешности систематические и случайные. Составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины в неизменных условиях, называется систематической. Составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же физической величины, называется случайной.
По причинам возникновения погрешности подразделяется на личные, методические и инструментальные.
К личным погрешностям относятся погрешности, возникающие при отсчетах по шкалам приборов, при отсчетах промежутков времени и т.п. В лабораторном практикуме эта составляющая, как правило, невелика и носит случайный характер.
Методическая погрешность возникает из–за недостаточной разработанности теории всех явлений, которые положены в основу измерений, и из–за неточности тех соотношений, которые используются для расчета искомой величины по данным эксперимента. В лабораторном практикуме эти соотношения точно описывают изучаемое явление, но они не всегда учитывают разнообразие сравнительно небольших влияний внешних факторов, изменение которых носит случайный характер (колебание температуры помещения, электрические и магнитные помехи, нестабильность источника тока и др.). По своим свойствам методические погрешности, встречающиеся в лабораторном практикуме, носят случайный характер.
|
|
|
Инструментальная погрешность измерения возникает из–за несовершенства средств измерений. В условиях лабораторного практикума инструментальная погрешность определяется классом точности приборов. Она носит как систематический, так и случайный характер.
Обнаруженная и оцененная систематическая погрешность исключается из результата измерения путем введения соответствующей поправки, в то время как случайная погрешность снижается путем многократных измерений физической величины. Поэтому основное внимание в лабораторном практикуме уделяют случайным погрешностям измерений.
При определении значения любой физической величины, истинное значение которой  , теоретически мыслимо получить бесконечный набор измеренных значений экспериментальных «точек»
, теоретически мыслимо получить бесконечный набор измеренных значений экспериментальных «точек»  Такой набор называется генеральной совокупностью значений. Для генеральной совокупности ее характеристики определяются довольно просто. Например, истинное значение в этом случае равно среднему значению, т.е.
Такой набор называется генеральной совокупностью значений. Для генеральной совокупности ее характеристики определяются довольно просто. Например, истинное значение в этом случае равно среднему значению, т.е.
 (3)
(3)
Просто вычисляется и характеристика разброса экспериментальных данных около Х – дисперсия D(x).
На самом деле в распоряжении исследования имеется не бесконечная, а ограниченная совокупность – ряд  измеренных значений величины
измеренных значений величины  . Эту ограниченную совокупность рассматривают как выборку из генеральной совокупности. Понятно, что ограниченный объем измерительной информации не позволяет в общем случае ожидать, что характеристики выборки в точности равны характеристикам генеральной совокупности. Задача обработки результатов измерений состоит в том, чтобы, пользуясь ограниченным объемом измерений (выборкой объема
. Эту ограниченную совокупность рассматривают как выборку из генеральной совокупности. Понятно, что ограниченный объем измерительной информации не позволяет в общем случае ожидать, что характеристики выборки в точности равны характеристикам генеральной совокупности. Задача обработки результатов измерений состоит в том, чтобы, пользуясь ограниченным объемом измерений (выборкой объема  из генеральной совокупности), наилучшим образом приближенно оценить истинное значение и разброс данных этого значения (дисперсию). Такими научными оценками являются соответственно средне арифметическое значение
из генеральной совокупности), наилучшим образом приближенно оценить истинное значение и разброс данных этого значения (дисперсию). Такими научными оценками являются соответственно средне арифметическое значение
|
|
|
 (4)
(4)
выборочная дисперсия отдельных измерений
 (5)
(5)
и выборочная дисперсия результата измерений
 (6)
(6)
где  отклонение отдельных значений от среднего
отклонение отдельных значений от среднего 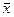 ;
;
 среднее квадратичное отклонение от среднего.
среднее квадратичное отклонение от среднего.
Как уже говорилось, нельзя ожидать, что  . Можно лишь утверждать, что с некоторой заранее заданной (доверительной) вероятностью погрешность измерений будет не больше некоторого числа
. Можно лишь утверждать, что с некоторой заранее заданной (доверительной) вероятностью погрешность измерений будет не больше некоторого числа  , т.е.
, т.е.
 (7)
(7)
где  характеризует точность оценки величины
характеризует точность оценки величины 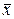 . Интервал
. Интервал  , равный
, равный  и заключающий в себе истинное значение
и заключающий в себе истинное значение  , называется доверительным. После обработки результат измерения должен быть записан в виде
, называется доверительным. После обработки результат измерения должен быть записан в виде
 (8)
(8)
Чтобы рассчитать  , должна быть задана (выбрана) заранее доверительная вероятность. В лабораторном практикуме по физике принято считать доверительную вероятность равной 0,96. Выбор такого значения вероятности типичен для физических измерений средней точности.
, должна быть задана (выбрана) заранее доверительная вероятность. В лабораторном практикуме по физике принято считать доверительную вероятность равной 0,96. Выбор такого значения вероятности типичен для физических измерений средней точности.
Для расчета доверительной точности необходимо знать не только доверительную вероятность, но и закон распределения случайной величины  . Этот закон вообще говоря, должен быть установлен для каждого конкретного ряда измерений. При большом числе измерений наиболее распространенным является нормальный закон распределения погрешности.
. Этот закон вообще говоря, должен быть установлен для каждого конкретного ряда измерений. При большом числе измерений наиболее распространенным является нормальный закон распределения погрешности.
На рис.1 представлена ось значений  , где за нуль (начало отчёта) выбрано среднее значение
, где за нуль (начало отчёта) выбрано среднее значение  Экспериментальные значения
Экспериментальные значения  могут быть положительными и отрицательными относительно выбранного нуля и теоретически могут располагаться в различных точках оси
могут быть положительными и отрицательными относительно выбранного нуля и теоретически могут располагаться в различных точках оси  , т.е. то нуля до бесконечности. Очевидно, что из n экспериментальных значений (“точек”) большинство их расположится симметрично относительно нуля и вблизи нуля, в то время как вероятность появления очень близких значений
, т.е. то нуля до бесконечности. Очевидно, что из n экспериментальных значений (“точек”) большинство их расположится симметрично относительно нуля и вблизи нуля, в то время как вероятность появления очень близких значений  при достаточно точных измерениях чрезвычайно мала.
при достаточно точных измерениях чрезвычайно мала.
Выберем на расстоянии  от нуля интервал
от нуля интервал  . Число
. Число  экспериментальных значений, попадающих в этот интервал, тем больше, чем больше
экспериментальных значений, попадающих в этот интервал, тем больше, чем больше  и объём выборки n:
и объём выборки n:  . Переходя к бесконечно малым значениям, получаем:
. Переходя к бесконечно малым значениям, получаем:
 (9)
(9)
Функция f ( ) называется функцией распределения вероятности. Эта функция характеризует вероятность появления отклонения
) называется функцией распределения вероятности. Эта функция характеризует вероятность появления отклонения  в зависимости от его величины.
в зависимости от его величины.
Распределение вероятности называют нормальным, если оно описывается дифференциальной функцией
|
|
|
 (10)
(10)
где σ– средне квадратичное отклонение случайной величины от среднего. График функции f( ) приведен на рис. 2. Расчеты показывают, что при нормальном распределении в интервал ±σ попадает 68% всех экспериментальных точек, а уже в интервал ±2σ –96% (то есть почти все). Как видно при выбранной доверительной вероятности 0,96 и при нормальном законе распределения отклонений экспериментальных значений от среднего, доверительный интервал равен
) приведен на рис. 2. Расчеты показывают, что при нормальном распределении в интервал ±σ попадает 68% всех экспериментальных точек, а уже в интервал ±2σ –96% (то есть почти все). Как видно при выбранной доверительной вероятности 0,96 и при нормальном законе распределения отклонений экспериментальных значений от среднего, доверительный интервал равен 
При малом числе измерений распределение подчиняется другому закону, а именно закону распределения Стьюдента. Это распределение при больших объемах выборки n переходит в нормальное распределение.
При принятых допущениях погрешность измерений, равную  (половине доверительного интервалу
(половине доверительного интервалу  ), можно интерпретировать как предельную погрешность. Её вычисляют по формуле
), можно интерпретировать как предельную погрешность. Её вычисляют по формуле
 , (11)
, (11)
в которой параметры ψ берут из табл. 3, рассчитанной из распределения Стьюдента для различных объёмов выборки n. Как видно, малое число n измерений приводит к тому, что одновременно вырастают ψ и подкоренное выражение. Тем самым увеличивается доверительный интервал, в пределах которого находится истинное значение измеряемой величины, а следовательно растёт погрешность  .
.
Таблица 3.
| n | ψ | n | ψ |
| 4,30 | 2,31 | ||
| 3,16 | 2,26 | ||
| 3,78 | 2,15 | ||
| 2,57 | 2,09 | ||
| 2,45 | 2,01 | ||
| 2,37 | 1,96 |

Модуль 1. Механика
Лабораторная работа №2
«Определение ускорения свободного падения»
Краткая теория
Гравитационное поле Земли или поле тяготения, (как и любое другое поле), это особый вид существования материи и представляет собой область пространства вокруг Земли (как массы), в котором на любую другую массу обнаруживается действие силы.
Эта сила определяется законом всемирного тяготения Ньютона:
 (1)
(1)
где  – гравитационная постоянная,
– гравитационная постоянная, 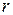 – расстояние между центрами взаимодействующей тел.
– расстояние между центрами взаимодействующей тел.
В данном случае  .
.
 Основными характеристиками гравитационного поля являются: напряжённость и потенциал.
Основными характеристиками гравитационного поля являются: напряжённость и потенциал.
В данной работе мы будем определять напряжённость поля – силовую характеристику его, которая численно равна силе, действующей на единицу массы в данной точке поля:

Напряжённость поля по размерности совпадает с ускорением и величина эта называется ускорением свободного падения.

 Ускорение свободного падения поля Земли или напряжённость поля можно найти, используя законы колебания математического маятника. Математическим маятником называется идеализированная система, состоящая из подвешенной длинной невесомой нерастяжимой нити с грузом на конце, размерами которого можно пренебречь. Период колебания математического маятника зависит от значения ускорения свободного падения в данном месте Земли:
Ускорение свободного падения поля Земли или напряжённость поля можно найти, используя законы колебания математического маятника. Математическим маятником называется идеализированная система, состоящая из подвешенной длинной невесомой нерастяжимой нити с грузом на конце, размерами которого можно пренебречь. Период колебания математического маятника зависит от значения ускорения свободного падения в данном месте Земли:
 (3)
(3)
где l – длина нити математического маятника.
Из формулы (3) найдём  .
.
 (4)
(4)
|
|
|


