Протокол лабораторной работы №6.

Таблица результатов градуирования газового термометра

Атмосферное давление =

Начальная температура =

Плотность жидкости в манометре =

Величина						Примечание

Вопросы для самопроверки к работе №6

1. В чём отличие газов от твёрдых и жидких тел? Какими основными параметрами определяется состояние газа?

2. Что такое давление? В каких единицах измеряют давление? Что принято за единицу давления в системе СИ?

3. Расскажите о порядке выполнения работы.

4. Что такое тепловое равновесие? Чем оно характеризуется?

5. Что такое температура? Что характеризует температура?

6. На каких опытных фактах основано измерение температуры?

7. В каких единицах измеряют температуру?

8. Что называют изопроцессом? Какие вы знаете изопроцессы? Напишите уравнение изопроцессов?

9. Сформулируйте словами уравнение состояния идеального газа.

10. Напишите уравнение Клапейрона–Менделеева. Сформулируете его словами.

11. Что называют универсальной газовой постоянной?

12. Расскажите об устройстве газового термометра.

 

Список рекомендуемой литературы

1. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. – М.: Высшая школа, 2009.

2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2010.

Материально–техническое обеспечение

Установка для лабораторной работы по молекулярной физике «Градуирование газового термометра»

 

Лабораторная работа №7.

«Определение показателя степени в уравнении Пуассона методом Клемана –Дезорма»

Краткая теория.

Процесс, происходящий при полной тепловой изоляции системы, т.е. без поступления и отдачи теплоты, называется адиабатным. Для создания адиабатных условий система должна быть идеально изолирована. Адиабатный процесс – это одно из проявлений I начала термодинамики, как закона сохранения и превращения энергии: при условии, что dQ = 0.

Если решить соотношение: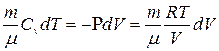

методом разделения переменных, то получим уравнение, описывающее закономерности адиабатного процесса:

(1)

(2)

Всякий реальный процесс можно рассматривать лишь как более или менее точное приближение к адиабатному. Близким к адиабатному можно считать быстрые процессы, т.е. протекающие столь быстро, что теплообмен системы с внешними телами не успевает осуществляться.

Уравнение (1) можно предоставить в виде , если ;

где – показатель степени адиабаты, С_Р – молярная теплоёмкость при постоянном давлении Р, С_v – теплоёмкость при постоянном объёме V, T – температура. Так как С_Р>С_V, то всегда .

Цель работы – определить показатель адиабаты γ для воздуха.

Описание установки.

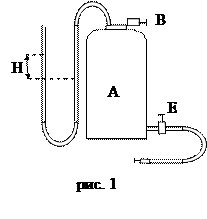
Установка, реализующая метод, показана на рис.1. Она состоит из сосуда А объёмом 10–12 литров, насоса С для закачки воздуха и манометрической U – образной трубки, в обеих коленах которой находится вода (рис.1). Соединение сосуда с окружающим воздухом осуществляется краном В.

До начала опыта краны В и Е (последний соединяет насос с сосудом) открыты.

Абсолютная температура воздуха в сосуде равна Т₀. Давление Р равна атмосферному Р ₀, таким образом параметры начального состояние Р₀,Т_{0 .}

В опыте создаются и анализируются следующие термодинамические состояния.

Состояние 1: кран В закрыт, кран Е открыт. С помощью насоса накачиваем воздух в сосуд. При этом давление и температура в сосуде повысится. Закрываем кран Е и ждём некоторое время, за которое произойдет теплообмен газа в сосуде с окружающей средой. В результате установится темпера Т₁=Т₀ и повышенное давление Р₁:

(3)

где H₁– измеряемое на опыте давление столба воды, соответствующее давлению в сосуде. Так как в манометрической трубке отсчет высоты ведётся по линейной шкале от некоторого нулевого значения 00, то

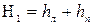
где h_л и h_п – расстояние от 00 до мениска жидкости соответственно в правом и левом колене трубки (рис.1). Параметры состояния равны Р₁,Т_{0 .}

Состояние 2. Кран Е закрыт, кран В быстро открывается. При этом воздух в сосуде адиабатически расширяется и давление достигает Р₀. За это время воздух охлаждается до температуры Т₂. Параметры состояния равны Р₀,Т_{2 .}

Состояние 3. Кран В после открытия столь же быстро закрывается; давление внутри сосуда начинает возрастать, т.к. охладившийся при адиабатном расширении воздух в сосуде вновь нагревается. Когда температура сравняется с температурой окружающего сосуд воздуха Т₃=Т₀, возрастает давление прекратится, достигнув некоторого значения

(4)

Параметры состояние 3 равны Р₃,Т₀.

Итак, при переходе из 1 состояния во 2 происходит адиабатное расширение, подчиняющейся закону Пуассона (1), которое запишем в форме . С учётом выражения (3) получаем:

(5)

Переход из состояния 2 в 3 происходит при постоянном объёме, т.е. согласно закону Гей– Люссака:

(6)

В уравнении (5) величина и (Т₀–Т₂)/Т₂<<1

Логарифмируя левую и правую части уравнения и учитывая, что при малых справедливо приближенное равенство 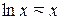, вместо (5)с учётом (6) получаем

(7)

Полученное уравнение позволяет определить значение γ по двум показаниям манометра (Η₁и Η₂).

Порядок выполнения работы

Закрыв плотно экран В, открывают кран Е и накачивают в сосуд (или выкачивают) воздух. Закрывают кран Е, ожидают, когда установится постоянное давление воздуха в сосуде. После этого производят отчет разности Η₁ уровеня жидкости в коленах манометра. Затем открывают на короткое время кран В, соединяют воздух сосуда с атмосферным воздухом и в момент, когда давление в сосуде будет равно атмосферному, закрывают кран. Снова ожидают, когда установится давление в сосуде после прошедшего адиабатного расширения (или сжатия).

Производят отчет по манометру величины Η₂ и вычисляют значение величины γ по формуле (7).

Опыт повторяют не менее пяти раз и из всех значений величины определяют среднее значение . Все результаты измерений записывают в таблицу. Рекомендуемая форма протокола выполнения лабораторной работы приведены ниже.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: