 |
Дифракция от щели в параллельных лучах
|
|
|
|
Пусть мы имеем монохроматическую плоскую волну, т.е. лучи света имеют одинаковую частоту и идут параллельно.
Поместим на пути лучей (рис.2) перпендикулярно к их направлению непрозрачную пластинку с узкой щелью АВ, края которой перпендикулярны плоскости чертежа. В этом случае АВ будет фронтом волны. На рис. 2 щель АВ сильно увеличена.
По принципу Гюйгенса каждая точка волновой поверхности АВ является источником новых элементарных сферических волн, и поэтому из всех точек щели световые колебания будут распространяться во всех направлениях, заходя и в область геометрической тени.
В направлении СМ, нормально к щели, все волны идут в одинаковых фазах. Если на пути этих лучей поставить линзу L, она соберет их в своем фокусе М. Так как линза не изменяет соотношение фаз (разности хода), проходящих через нее лучей, то в точку М все лучи придут с одинаковой фазой. Такие лучи при сложении усилят друг друга, и на экране в направлении СМ мы увидим светлую полоску, которую называют н у л е в ы м м а к с и м у м о м.
Рассмотрим теперь параллельный пучок лучей, который распространяется от щели под некоторым углом j к нормали и собирается линзой в точке Е. Из точки Е проведем несколько дуг, начиная от края щели (точки А) на расстоянии 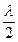 друг от друга, где
друг от друга, где 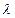 – длина волны падающего света. Эти дуги разобьют поверхность АВ на зоны Френеля, число которых зависит от ширины щели и выбранного направления, определяемого углом j.
– длина волны падающего света. Эти дуги разобьют поверхность АВ на зоны Френеля, число которых зависит от ширины щели и выбранного направления, определяемого углом j.
На рис. 2. ВР = 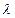 следовательно таких зон Френеля в АВ две– АС и СВ.
следовательно таких зон Френеля в АВ две– АС и СВ.
Пусть ширина щели равна АВ = а, тогда разность хода крайних лучей
ВР = a×Sinj и число зон Френеля m определяется из равенства:
 a×Sin j a×Sin j
| (3) |
Пользуясь методом Френеля, можно сделать следующий вывод.
|
|
|
В тех направлениях, в которых разность хода крайних лучей равна целому числу волн, т.е. четному числу полуволн, число зон Френеля будет четное, каждая пара зон погасится, и мы увидим на экране темные полосы – м и н и м у м ы. Математическое условие минимума можно записать равенством:
а Sin j = 2 k  , или Sin j = , или Sin j = 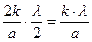 , ,
| (4) |
где к – любое целое число, определяющее порядок соответствующего минимума, к – 1, 2, 3.....В тех направлениях, в которых разность хода крайних лучей равна нечетному числу полуволн, число зон Френеля будет нечетное, и мы увидим на экране светлые полосы, м а к с и м у м ы, Математически условие максимума можно записать равенством:
a Sinj = (2k + 1) 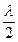 или Sinj = или Sinj = 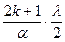
| (5) |
где k – любое целое число, определяющее порядок соответствующего максимума, k = 1, 2, 3 …
Следовательно, при нормальном падении параллельного пучка лучей на узкую щель мы увидим на экране за щелью центральную светлую полоску и симметрично расположенные по обе стороны темные и светлые полоски убывающей яркости.
На рис. 3 показано примерное распределение яркости (ось ординат) в зависимости от синуса угла отклонения (ось абсцисс) для дифракционной картины даваемой одной щелью.
Из равенства (5) видно, что:
1) при постоянной длине волны с уменьшением ширины щели увеличивается угол отклонения, т.е. увеличивается расстояние между светлыми полосками;
2) при постоянной ширине щели с увеличением длины волны увеличивается угол отклонения, т.е. лучи с большей длиной волны дальше отклоняются от нулевого максимума.
Из этого следует, что если на щель падают не монохроматические (не одноцветные) лучи, а например, белые лучи, в состав которых входят волны всевозможных длин от 0,38 до 0,76 мкм, то мы получим на экране центральную белую полоску, а по сторонам симметрично расположатся дифракционные спектры 1, 2, 3... и т.д. порядков, разделенные темными промежутками.
|
|
|
Дифракционная решетка
Для получения ярких дифракционных спектров применяются дифракционные решетки. Дифракционная решетка представляет собою совокупность большого числа узких параллельных щелей одинаковой ширины, расположенных на равных расстояниях друг от друга. Простейшим примером дифракционной решетки является стеклянная пластинка, на которой делительной машиной нанесен ряд параллельных штрихов. Места, прочерченные машиной являются практически непрозрачными промежутками. Неповрежденные части пластинки играют роль щелей.
Рассмотрим дифракционную картину, даваемую решеткой. Картина дифракционных максимумов и минимумов, даваемых одной щелью, не зависит от положения щели, т.е. если щель переместить параллельно самой себе, то параллельно переместится и вся дифракционная картина. Поэтому, если в пластинке проделаны одинаковые параллельные щели (рис.4), то они дадут одинаковые дифракционные картины. Если на пути лучей, распространяющихся от щелей решетки, поместить линзу, а в фокальной плоскости линзы экран, то на экране в одну точку соберутся все параллельные лучи, идущие под одним и тем же углом j к нормали.
Лучи идущие под другим углом, соберутся в другой точке. Освещенность каждой точки экрана будет зависеть как от интенсивности света, даваемого каждой щелью в отдельности, так и от результата интерференции лучей, прошедших через равные щели. В тех местах, где каждая из щелей дает минимум, будет минимум и при нескольких щелях. Но в тех местах, где каждая из щелей дает свет, не обязательно будет свет и при нескольких щелях. В некоторых направлениях лучи света, прошедшие через разные щели, могут вследствие интерференции гасить друг друга и давать д о б а в о ч н ы е, к даваемым каждой щелью, минимумы. Точно также в других направлениях лучи, складываясь, могут усиливать друг друга, давать максимумы.
Обозначим на рис. 4 ширину щели АВ = а, ширину непрозрачного промежутка ВС = в. Расстояние а + в = с называют п е р и о д о м решетки или п о с т о я н н о й решетки.
В направлении нормали лучи идут в одинаковой фазе и при сложении (на рис.4 линза не показана) усилят друг друга, дадут светлую полоску, которую называют нулевым максимумом.
|
|
|
Возьмем лучи., распространяющиеся от щелей под некоторым углом j к нормали, и проведем линию АР перпендикулярно к направлению лучей. От этой линии до экрана лучи, распространяющиеся от щелей, будут проходить одинаковые расстояния. Но до этой линии пути, пройденные лучами, различны. Разность хода лучей, идущих от соответственных точек соседних щелей, т.е. лучей, начинающихся у тождественных точек равна:
| d = РС = АС × Sin j = с Sin j | (6) |
На рис. 4 ряд таких соответственных точек показан стрелками.
Если разность хода d равна целому числу волн, т. е. четному числу полуволн, то все лучи, идущие от одной щели, будут при сложении усиливаться лучами, идущими от с о о т в е т с в е н н ы х точек соседних щелей и в направлении, определяемом равенством:
с Sin j = 2k 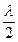 или Sin j = или Sin j = 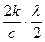 , ,
| (7) |
мы увидим светлую полоску – максимум. Величина к, равная любому целому числу начиная с 1, показывает порядок максимума. Из этого равенства следует, что положение максимумов не зависит от числа щелей решетки, а зависит только от длины волны падающего света и постоянной решетки.
Если разность хода d будет равна нечетному числу полуволн, то все лучи щели при сложении погасятся лучами, идущими от с о о т в е т с в е н н ы х точек соседних щелей. В направлении определяемом равенством
с Sin j = (2 k + 1) 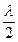 , или Sin j = , или Sin j = 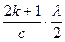 , ,
| (8) |
мы увидим темную полоску, добавочный минимум.
Из формулы (7) следует, что лучи различной длины волны будут иметь максимум в различных направлениях. Поэтому, если на дифракционную решетку падает белый луч, то решетка разложит его, и на экране мы увидим дифракционный спектр, обращенный к центральной полосе фиолетовой линией.
Дифракционная решетка находит большое применение в спектральном анализе, обладая рядом преимуществ по сравнению с призматическим спектрографом. Разрешающая способность спектрографов с дифракционной решеткой выше чем у спектрографов призматических. Для определения длины волны достаточно знать период решетки и расстояние от решетки до экрана, предварительной градуировки спектрометра не требуется.
|
|
|
Дифракционной решеткой может служить прозрачная жидкость или газ, в которых распространяется ультразвуковые волны. В этом случае по дифракционной картине можно определить длину ультразвуковых волн и скорость их распространения. Дифракция рентгеновских лучей при прохождении через кристалл позволяет определить структуру кристалла.
|
|
|


