 |
Протокол лабораторной работы №28
|
|
|
|
Результаты измерений записывают в таблицу. Таблица результатов по определению чувствительности
фотоэлемента типа Фоточувствительная поверхность S=
Сила света лампы J =
| № п/п | ||||||||||
| R | ||||||||||
| i | ||||||||||
| E | ||||||||||
| Ф |
Обрабатывают результаты измерений.
Зная силу света J лампы при данном напряжении и расстояние от лампы до фотоэлемента, находят освещенность фотоэлемента по закону освещенности
Е =  . Зная освещенность и светочувствительность площадь фотоэлемента, (она указана в работе), находят световой поток, падающий на фотоэлемент
. Зная освещенность и светочувствительность площадь фотоэлемента, (она указана в работе), находят световой поток, падающий на фотоэлемент
Ф = ЕS
Зная световой поток Ф и силу фототока i, строят график зависимости i от Ф. Из графика находят чувствительность фотоэлемента к = 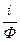 .
.
Вопросы для самопроверки к работе №28
Список рекомендуемой литературы
1. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. – М.: Высшая школа, 2009.
2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2010.
Материально–техническое обеспечение
1. Установка для лабораторной работы по оптике «Определение чувствительности фотоэлемента».
2. Программа для моделирования лабораторной работы на компьютере.
Модуль 5. Основы физики атома и атомного ядра
Лабораторная работа №26
«Градуирование спектроскопа и определение постоянной Планка»
Краткая теория
Спектры излучения
Световое излучение всех естественных источников света имеют более или менее сложный состав. Сложность состава так называемого белого света, даваемого солнцем или раскаленными твердыми и жидкими телами, легко обнаружить с помощью опыта Ньютона. Через узкую равномерно освещенную щель 0 /рис.1/ пропускают пучок лучей белого света и направляют их на прозрачную призму.
|
|
|
На рисунке щель расположена горизонтально, перпендикулярно плоскости чертежа. Грани призмы также перпендикулярны чертежу. Если пучок лучей после выхода из призмы падает на белый экран B, то на экране появляется вертикальная цветная полоска. На рис. 1 показаны только крайние ограничивающие пучки: красный и фиолетовый. Любое, параллельное щели, сечение этой полосы окрашено в один определенный цвет. Но различные, параллельные друг другу, сечения окрашены в различные цвета, постепенно переходящие друг в друга. Полученная цветная полоса называется с п е к т р о м исследуемого источника света.
С помощью специальных опытов было обнаружено, что в состав излучения большинства источников, помимо видимых лучей, входит большое количество лучей не воспринимаемых нашим глазом. Лучи, имеющие длину волны большую, чем красные лучи, преломляются меньше красных лучей и лежат за красным концом спектра, их называют и н ф р а к р а с н ы м и и обнаруживают по тепловому действию. Лучи имеющие длину волны меньшую, чем фиолетовые, преломляются больше фиолетовых лучей и лежат за фиолетовой частью спектра, их называют у л ь т р а ф и о л е т о в ы м и и обнаруживают по химическому действию.
Совокупность лучей, испускаемых данным источником, называется с п е к т р о м и з л у ч е н и я источника. Спектры раскаленных твердых или жидких тел являются н е п р е р ы в н ы м и или сплошными. Спектры светящихся газов состоят из отдельных цветных линий или групп цветных линий, также спектры называются л и н е й ч а т ы м и. Спектры светящихся газов зависят от химической природы газа. Каждый газ или пар дает свой, характерный только для него спектр. Поэтому спектр светящегося газа дает возможность делать заключение об его химическом составе.Метод исследования, позволяющий по спектру излучения судить о химической природе тела, называется с п е к т р а л ь н ы м а н а л и з о м.
|
|
|
Дисперсия света
Проследим причины образования спектра. С точки зрения волновой теории всякий колебательный процесс можно характеризовать частотой колебаний, амплитудой и фазой. Амплитуда колебаний, точнее ее квадрат, определяет энергию колебаний. Фаза играет основную роль в явлении интерференции. Цвет всех лучей связан с частотой колебаний. В безвоздушном пространстве лучи любой частоты или длины волны распространяются с одинаковой скоростью. На основании соотношения с=ln, частота n обратно пропорциональна длине волны l (с=3.108м/с – скорость света в вакууме).
Опыт показывает, что во всех более или менее плотных средах волны различной длины распространяются с различной скоростью. в силу этого, показатель преломления, представляющий отношение скорости с света в вакууме к скорости  в данной среде:
в данной среде:
n = 
| (1) |
будет в одной и той же среде иметь различные значения для волн различной длины. Таким образом, входя в призму и выходя из нее, составные части белого луча испытывают различное преломление и выходят расходящимся цветным пучком.
Угол q между гранями призмы /рис.1/, через одну из которых свет проходит, а через другую входит, называется п р е л о м л я ю щ и м
у г л о м п р и з м ы. Противоположная ему грань называется о с н о в а н и е м п р и з м ы. При прохождении через призму лучи отклоняются к основанию призмы. Опыт Ньютона показывает, что среди лучей видимого света наименее преломляемыми являются лучи красного цвета, за ними, по степени преломляемости, идут оранжевые, желтые, зеленые, голубые, синие, фиолетовые лучи. nфиол> nкр
Зависимость показателя преломления среды от длины волны света, а также оптические явления, в которых эта зависимость обнаруживается, носят названия д и с п е р с и я света, а получаемую на экране цветную полосу называют дисперсионным спектром. Дисперсия называется н о р м а л ь н о й, если показатель преломления возрастает с уменьшением длины. В противном случае дисперсия называется а н о м а л ь н о й.
|
|
|
После двухкратного преломления на входной и выходной гранях призмы луч оказывается отклоненным от первоначального направления на угол d, называемый углом о т к л о н е н и я. Угол d имеет наименьшее значение при симметричном ходе лучей, т.е. когда AB параллельно основанию призмы. Угол j между крайними лучами дисперсионного спектра называется у г л о м дисперсии. Количественной мерой дисперсии света является отношение изменения показателя преломления Dn к соответствующему изменению длины световой волны Dl:
Д = 
На явлении нормальной дисперсии основано действие призматических спектроскопов и спектрографов.
Сериальные формулы
Вопрос о спектрах представляется одним из центральных в современной физике: сюда относятся, например, такие обширные отделы современной физики, как учение о строении атома и молекул, учение об изотопах и др.
Линейчатые спектры состоят из ряда тонких прямых линий, которые могут быть расположены как в видимой, так и в инфракрасной и в ультрафиолетовой частях спектра. В видимой части они представляются светлыми линиями на темном фоне, причем цвет линии одинаков с цветом того места сплошного спектра, которые они занимают.
Линейчатый спектр показывает, что данное вещество испускает лучи не всевозможных длин волн / хотя бы в определенных пределах, но только лучи как бы избранные по каким–то правилам или законам. В течение долгого времени ученые тщетно старались найти какие–либо закономерности в распределении спектральных линий различных элементов, т.е. найти зависимость длины l или частоты n от какого–либо параметра.
Такую зависимость установил в 1885 году Бальмер для спектра водорода. Спектр водорода в видимой части из пяти линий: красной, зеленой, синей, фиолетовой 1 и фиолетовой 2.
Бальмер эмпирически установил, что длина волны спектральных линий водорода с большой точностью определяется формулой:
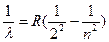 или n = cR или n = cR 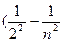 ), ),
| (2) |
где R – постоянное число, получившее название постоянной Ридберга
R= 10967758  ; сR = 3,29 × 1015 1/сек;
; сR = 3,29 × 1015 1/сек;
n – целые числа, начиная с 3–х;
|
|
|
l – длина волны;
 – получило название в о л н о в о е число
– получило название в о л н о в о е число  ;
;
n – частота колебаний;
С – скорость распространения света в вакууме.
Подставляя в формулу (2) n = 3 получим значение длины волны для красной линии водорода; при n = 4 – для зеленой; при n = 5 – для синей и т.д.
Ряд спектральных линий, для которых l (или n) связаны между собой одной формулой, называется серией спектральных линий, а сама формула с е р и а л ь н о й.
Серия водородных линий, определяемых формулой (2), называется серией Бальмера. Она продолжается в ультрафиолетовой части спектра. Всего в ней было найдено 29 линий (от n=3 до n=31).
Были получены и другие сериальные формулы водородных линий. В общем случае сериальная формула для водорода имеет вид:
 или n = сR ( или n = сR ( ) )
| (2/) |
Известны серии Лаймана при n1=1, для линий в ультрафиолетовой части спектра. Серия Пашена при n1 = 3, для линий в инфракрасной части спектра. Известны и другие серии при
n1 = 4, n1 = 5, n1 = 6.
Р. Ридберг показал, что в линейчатых спектрах не только водорода, но и других элементов, наблюдаются спектральные серии, причем частоты n всех линий данной серии удовлетворяют соотношение:
| n = Т (n1) – Т (n2) | (3) |
где n1 и n2 – целые числа, причем n2  n1+1. Для данной серии n1 имеет постоянное значение. Изменение числа n дает все линии данной серии. Функции T (n1) и T (n2) называются спектральными т е р м а м и. В. Ритц установил справедливость положения названного комбинационным принципом Ритца: частоты спектральных линий излучения любого атома могут быть представлены в виде разности двух термов; составляя различные комбинации термов можно найти все возможные частоты спектральных линий этого атома. Например, беря разность термов для зеленой и красной линии водорода, получим:
n1+1. Для данной серии n1 имеет постоянное значение. Изменение числа n дает все линии данной серии. Функции T (n1) и T (n2) называются спектральными т е р м а м и. В. Ритц установил справедливость положения названного комбинационным принципом Ритца: частоты спектральных линий излучения любого атома могут быть представлены в виде разности двух термов; составляя различные комбинации термов можно найти все возможные частоты спектральных линий этого атома. Например, беря разность термов для зеленой и красной линии водорода, получим:
R (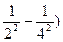 – R (
– R ( = R (
= R (
первую линию водорода серии Пашена. При неограниченном возрастании n частоты n всех серий спектра сходятся к соответствующим границам. Граничные частоты серии водородного спектра Т (n) =  .
.
Все усилия физиков вывести сериальные формулы из общих законов электромагнитной теории света оказалась безуспешным. Не только вывод формул, но даже простое качественное описание возникновения линейчатых спектров оказалось не под силу старой классической физике, хотя предложенная Резерфордом ядерная модель строения атома и была, в основном, правильной.
|
|
|


