 |
Циклы. Тепловые и холодильные машины. КПД цикла Карно для идеального газа
|
|
|
|
Циклическим (круговым) процессом или циклом называется процесс, в котором начальное и конечное состояния системы совпадают. В цикле, изображенном на рис. 8.1, на участке 1-а-2 система совершает положительную работу, а возвращаясь в исходное состояние по пути 2-b-1 – отрицательную, но меньшую по абсолютной величине. При этом полная работа, совершенная за цикл, положительна. Она равна площади фигуры 1-a-2-b-1, охватываемой циклом на P-V диаграмме.

| 
|
| Рис. 8.1 | Рис. 8.2 |
Так как внутренняя энергия U является функцией состояния, ее изменение в циклическом процессе равно нулю (D U = 0). Тогда из первого начала термодинамики следует, что полная работа А, совершаемая системой за цикл, равна полному количеству тепла Q, полученному системой в цикле. Если работа цикла А положительна, то говорят, что цикл проходится в прямом направлении (по часовой стрелке). Такие циклические процессы можно использовать для создания тепловых машин – устройств, совершающих механическую работу за счет тепла, получаемого от тепловых резервуаров.
Тепловая машина включает в себя рабочее тело, т.е. систему, осуществляющую цикл и совершающую работу, и как минимум два тепловых резервуара, с которыми рабочее тело обменивается теплом.
Простейшая тепловая машина схематически изображена на рис. 8.2. Тепловые резервуары, от которых рабочее тело в прямом цикле (при котором А > 0), получает положительное количество тепла, называют нагревателями. Резервуары, от которых получено отрицательное количество тепла, называют холодильниками. Сумму положительных количество теплоты, полученных системой от нагревателей на всех этапах цикла, принято обозначать Q + = Q 1, а сумму отрицательных теплот, полученных от холодильников Q - = - Q 2. При этом Q 2 называют количеством тепла, отданного системой холодильнику (Q 2> 0).
|
|
|
Работа цикла равна алгебраической сумме количеств теплоты, полученных системой на всех этапах цикла
A = Q + + Q - = Q 1 – Q 2.
Коэффициентом полезного действия (КПД) цикла называется отношение работы А, совершенной системой при прохождении цикла, к количеству тепла Q1 º Q+, полученному системой от нагревателя
 . (8.1)
. (8.1)
Рассчитанный таким способом КПД h иногда называют термодинамическим, чтобы подчеркнуть его отличие от технического КПД, который всегда оказывается меньше из-за различных потерь, сопровождающих работу реальных машин.
Если направление обхода цикла изменить на противоположное, то работы и количества теплоты на всех его этапах изменят знак. Такой цикл называется обратным. При прохождении обратного цикла полная работа А обр, совершенная рабочим телом, отрицательна А обр = - А (внешние силы, действующие на систему, совершают положительную работу А). Система получает положительное количество тепла от холодильника и отдает тепло нагревателю.
По обратному циклу работают холодильные машины. Они потребляют механическую энергию, отнимают тепло у сравнительно холодного тела и передают тепло более нагретому телу. Если целью работы машины является нагревание более теплого тела (например, повышение температуры воздуха в комнате за счет тепла, отобранного у уличного воздуха) она называется тепловым насосом. Его эффективность определяется производительностью теплового насоса xТ.Н, которая равна отношению количества теплоты, полученной нагреваемым телом, к затрачиваемой на это работе
 .
.
Полезный эффект превышает затраченную работу, x Т..Н > 1, но никакого нарушения закона сохранения энергии здесь, конечно, нет. Работа внешних сил не превращается в тепло, а обеспечивает «перекачку» тепла от тела менее нагретого к телу более нагретому.
|
|
|
Если ставится задача отбора тепла у более холодного тела, машину называют холодильным агрегатом. Ее эффективность характеризуется холодильным коэффициентом xХ, равным отношению отобранного тепла к затраченной работе
 .
.
Коэффициенты x Т.Н и x Х используются, в основном, в технических приложениях термодинамики.
Из различных циклических процессов особое значение в термодинамике имеет цикл Карно. Он состоит из двух изотерм (a-b и c-d) и двух адиабат (b-c и d-a) (рис 8.3).
 Рис. 8.3
Рис. 8.3
|
Найдем КПД цикла Карно, рабочим веществом которого является один моль идеального газа. На участке а-b рабочее тело находится в тепловом контакте с нагревателем, имеющим температуру Т 1. Производится квазистатическое изотермическое расширение от объема V a до объема V b. При этом газ получает от нагревателя количество тепла Q ab. Так как внутренняя энергия идеального газа зависит только от температуры и при изотермическом процессе не меняется, то, согласно первому началу термодинамики,
 .
.
На этапе b-c происходит адиабатическое (Q bc = 0) расширение газа. Его температура при этом понижается. Когда она достигнет температуры холодильника Т 2, газ приводится в тепловой контакт с холодильником, и начинается процесс изотермического сжатия c-d. Газ при этом совершает отрицательную работу А cd и получает отрицательное количество тепла Q cd (отдает холодильнику положительное количество тепла)
 .
.
Далее на участке d-a происходит адиабатическое (Q da = 0) сжатие газа, сопровождающееся ростом температуры. В состоянии а температура станет равной Т 1 и цикл завершится.
Из проведенного рассмотрения этапов цикла видно, что положительное количество тепла газ получает только на участке a-b, т.е. Q 1 = Q ab. Отрицательное количество тепла газ получает на участке c-d, значит отданное холодильнику тепло Q 2=- Q cd. Тогда КПД цикла
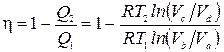 .
.
Запишем уравнения адиабат b-c и d-a, учитывая, что Т а = Т b = T 1, T c = T d = T 2,
 .
.
Разделив одно уравнение на другое, получим  . Тогда КПД цикла Карно для идеального газа
. Тогда КПД цикла Карно для идеального газа
 . (8.2)
. (8.2)
Отметим, что из выражения для КПД, записанного в виде  , следует
, следует
 . (8.3)
. (8.3)
Соотношение (8.3) представляет собой частный случай равенства Клаузиуса (подробнее см. § 13).
|
|
|


