Термодинамическая шкала температур

Теорема Карно позволяет построить температурную шкалу, совершенно не зависящую от индивидуальных особенностей термометрического вещества и устройства термометра. Эта шкала температур предложена У. Томсоном (лордом Кельвином) в 1848 г. Она строится следующим образом. Пусть t ₁ и t ₂ температуры нагревателя и холодильника, измеренные каким-либо термометром. Тогда, согласно теореме Карно, КПД цикла Карно

,

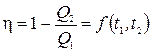где f (t ₁, t ₂) – универсальная функция выбранных эмпирических температур t ₁ и t ₂. Ее вид совершенно не зависит от конкретного устройства машины Карно и от рода используемого рабочего вещества. В дальнейшем нам удобнее будет рассматривать более простую универсальную функцию температур

.

Эта функция легко выражается через f (t ₁, t ₂). Чтобы определить общий вид функции j(t ₁, t ₂), рассмотрим три тепловых резервуара, температуры которых поддерживаются постоянными. Эмпирические температуры этих резервуаров обозначим t ₁, t ₂, t ₃ соответственно. Используя их в качестве нагревателей и холодильников, проведем три цикла Карно (a-b-c-d, d-c-e-f, a-b-e-f), изображенные на рис. 11.1.

При этом температуры на изотермах a-b, d-c, f-e равны t ₁, t ₂, t ₃, а абсолютные значения полученных на изотермах теплот равны Q ₁, Q ₂, Q ₃ соответственно. Для циклов a-b-c-d и d-c-e-f можно написать

, .

Исключая отсюда Q ₂, получим

.

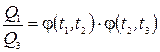Объединенные вместе, эти два цикла эквивалентны одному циклу Карно a-b-e-f, т.к. изотерма c-d проходится дважды в противоположных направлениях, и ее можно исключить из рассмотрения. Следовательно,

.

Сравнивая это выражение с предыдущим, получим

.

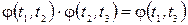Так как правая часть не зависит от t ₂, то данное соотношение может выполняться при любых значениях аргументов t ₁, t ₂, t ₃ только если функция j(t ₁, t ₂) имеет вид

.

Таким образом, j(t ₁, t ₂) представляет собой отношение значений одной и той же функции Q(t) при t = t ₁ и t = t ₂. Так как величина Q(t) зависит только от температуры, она сама может быть принята за меру температуры тела. Величина Q называется абсолютной термодинамической температурой. Отношение двух термодинамических температур Q₁ и Q₂ определяется соотношением

. (11.1)

Тогда КПД цикла Карно может быть записан в виде

. (11.2)

Сравнивая выражение (11.2) с КПД цикла Карно для идеального газа (8.2) можно убедиться, что отношения термодинамических и идеально-газовых температур тепловых резервуаров в цикле Карно совпадают.

Отношение Q₁/Q₂ в принципе может быть найдено экспериментально. Для этого надо измерить абсолютные значения теплот Q ₁ и Q ₂, которые получает рабочее тело в цикле Карно от тепловых резервуаров с температурами Q₁ и Q₂. Однако значением этого отношения сами температуры Q₁ и Q₂ еще не определяются однозначно.

Для однозначного определения абсолютной термодинамической температуры следует приписать какой-либо температурной точке определенное значение Q, а затем с помощью соотношения (11.1) вычислять температуру любого другого тела. Исходя из точности, с которой удается воспроизводить те или иные характерные температуры, в качестве основной реперной точки была выбрана тройная точка воды, т.е. температура, при которой в равновесии находятся лед, вода и водяной пар (давление при этом Р _тр = 4,58 мм. рт. ст.). Этой температуре приписано значение Т _тр = 273,16 К точно. Такая величина реперной температуры выбрана для того, чтобы обеспечить совпадение термодинамической температуры с идеально-газовой в пределах применимости последней.

Построенная температурная шкала называется абсолютной термодинамической шкалой температур (шкалой Кельвина).

Машина Карно позволяет лишь принципиально построить температурную шкалу. Для практических измерений температуры она непригодна. Однако многочисленные следствия второго начала термодинамики и теоремы Карно позволяют найти поправки к показаниям реальных термометров, приводящие эти показания к абсолютной термодинамической шкале. Для этой цели можно использовать любое точное термодинамическое соотношение, в которое помимо температуры Т входят только экспериментально измеримые величины.