Построение линейной, квадратичной, степенной регрессий и их уравнений

СОДЕРЖАНИЕ

Введение.. 3

1. Постановка задачи.. 4

2. Построение поля корреляции и выдвижение гипотезы о форме связи.. 5

2.1. Организация исходных данных. 5

3. Построение линейной, квадратичной, степенной регрессий и их уравнений.. 7

4. Определение надежности моделей и адекватности построенных регрессий.. 10

4.1 Анализ линейного уравнения регрессии. 10

4.2 Анализ квадратичного уравнения регрессии. 12

4.3 Анализ степенного уравнения регрессии. 14

5. Расчет индекса корреляции для нелинейных моделей 16

6. Построение доверительной области.. 17

7.Оценка полученных результатов и их обобщение. 19

Заключение.. 20

Введение

 

Целью данной лабораторной работы является исследование парных эконометрических зависимостей средствами Statiatica 6.1, то есть построение приблизительной аналитической зависимости – простой (парной) регрессии, которая представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция одной независимой (объясняющей) переменной х.

Исходные данные для анализа содержатся в матрице наблюдений, состоящей из двух столбцов, один из которых содержит значение зависимой величины (функции отклика), а другой – значение независимого признака.

Постановка задачи

 

Для набора экономических или финансовых показателей выполнить:

 

1) построение поля корреляции и выдвинуть гипотезу о форме связи;

2) построение линейной, квадратичной, степенной регрессий и уравнение соответствующее выдвинутой гипотезе;

3) отображение на поле корреляции теоретических значений по каждой из моделей;

4) определение надежности каждого уравнения и значимость всех параметров регрессий;

5) расчет средних коэффициентов эластичности для каждой модели;

6) расчет для нелинейных форм индекса корреляции и оценить тесноту связи, исследуемых величин;

7) построение доверительной области для каждой модели;

8) оценку средней относительной ошибки аппроксимации для каждой модели;

9) оценку полученных результатов и их обобщение.

 

Исходные данные представлены в таблице 1.

 

Таблица 1 - Валовый сбор овощей в хозяйствах всех категорий и индексы цен производителей овощей за период с 2000 по 2005 гг.

Показатель	Значения показателя
Валовый сбор овощей, млн т.	12,5	13,3		14,8	14,6	15,2
Индекс цен производителей овощей, %	119,4		140,6	115,2	118,5

 

 

Построение поля корреляции и выдвижение гипотезы о форме связи

Организация исходных данных

 

Качественную оценку зависимости валового сбора овощей и индекса цен производителей выполним графическим методом с помощью поля корреляции. Построим диаграмму рассеяния (см. рис.2.1):

 

Таблица 2.1 – Исходные данные для анализа зависимости

	Индекс цен производителей	Валовый сбор овощей
	119,4	12,5
		13,3
	140,6
	115,2	14,8
	118,5	14,6
		15,2

 

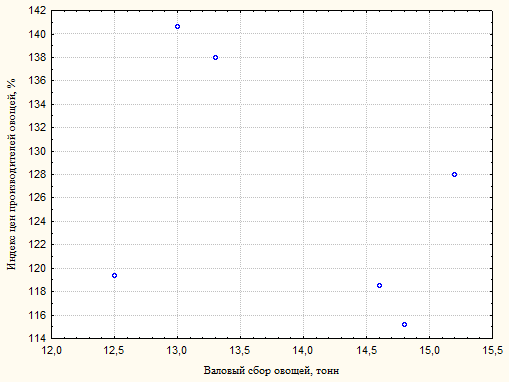
Рисунок 2.1 - Поле корреляции для

валового сбора овощей и индекса цен производителей

 

Предположим, что для описания закономерности между валовым сбором овощей и индексом цен можно использовать линейную зависимость, определенную уравнением

Валовый сбор овощей = a + b ∙ (Индекс цен производителей).

 

Построение линейной, квадратичной, степенной регрессий и их уравнений

 

 

Построим диаграмму рассеяния с линейной регрессионной линией и уравнением (см. рис. 3.1):

y = 179,923 − 3,835∙x, (3.1)

 

где x – объем сбора овощей в хозяйствах, млн. тонн;

y – индекс цен производителей овощей, %.

Таким образом, увеличение объема сбора овощей на 1 млн. тонн приведет к уменьшению индекса цен на 3,835 %.

 

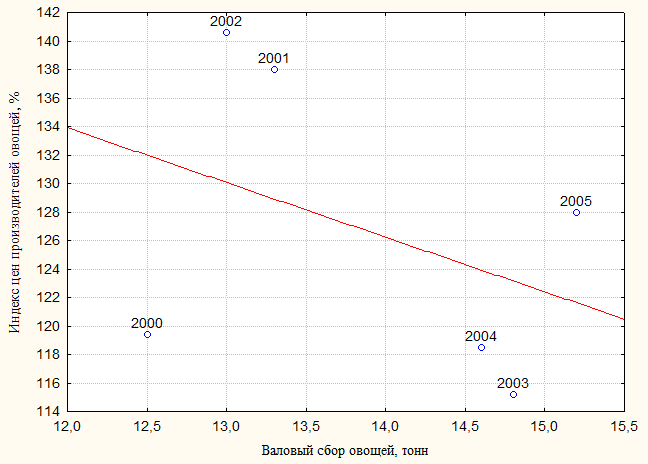
Рисунок 3.1 - Результаты нелинейного оценивания с помощью

диаграммы рассеяния с линейной регрессионной линией и уравнением

 

Аналогично построим диаграммы рассеяния и уравнения для квадратичной и степенной функций.

 

Итак, для квадратичной функции:

 

y = -837,55 + 143,711∙ 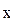− 5,3205∙ 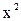. (3.2)

 

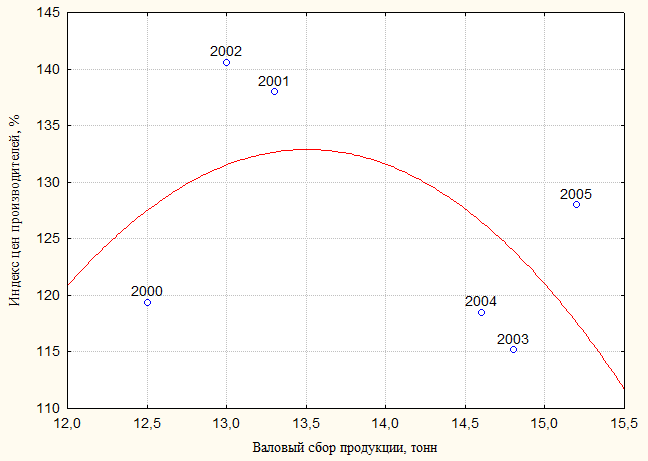
Рисунок 3.2 - Результаты нелинейного оценивания с помощью

диаграммы рассеяния с квадратичной регрессионной линией и уравнением

 

Для степенной функции:

 

y = 364,823∙ 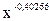. (3.3)

 

 

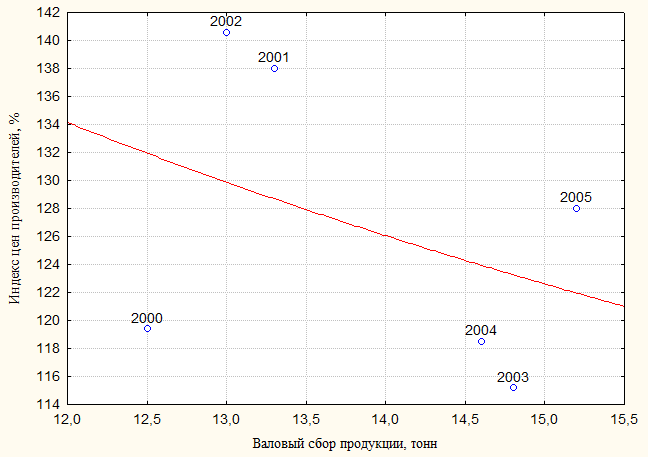
Рисунок 3.3 - Результаты нелинейного оценивания с помощью

диаграммы рассеяния со степенной регрессионной линией и уравнением

 

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: