 |
Расчет средних коэффициентов эластичности
|
|
|
|
При известных уравнениях линейной, степенной и квадратичной регрессии для сбора овощей и индекса цен легко определить коэффициенты эластичности:
– для линейной модели:
,
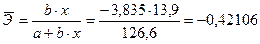т.е. изменение валового сбора овощей на 1% приведет к уменьшению индекса цен в среднем на 0,42 %;
– для квадратичной модели:
0,02242,
т.е. изменение валового сбора овощей на 1% приведет к увеличению индекса цен в среднем на 0,022 %;
– для степенной модели:
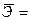–0,40266,
т.е. изменение валового сбора овощей на 1% приведет к уменьшению индекса цен в среднем на 0,402 %.
Расчет индекса корреляции для нелинейных моделей
Качество нелинейной регрессии оценивается с помощью индекса корреляции:
.
Величина данного показателя находится в пределах от 0 до 1, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение.
а) для квадратичной модели:
R= 
= 0,51.
б) для степенной модели:
R= = 0,384.
Получим, что индекс корреляции для обоих моделей далек от единицы и связь не является тесной. Но тем не менее, для квадратичной модели связь является более тесной.
Построение доверительной области
Диаграмма рассеяния с построенной доверительной областью для линейной модели представлена на рис. 6.1.
Рисунок 6.1 - Вид диаграммы рассеяния с доверительной
областью при доверительной вероятности в 95% для линейной модели
Вывод: в доверительную область для линейного уравнения регрессии для описания зависимости между валовым сбором овощей и индексом цен на них входят все точки.
Диаграмма рассеяния с построенной доверительной областью для линейной модели представлена на рис. 6.2.
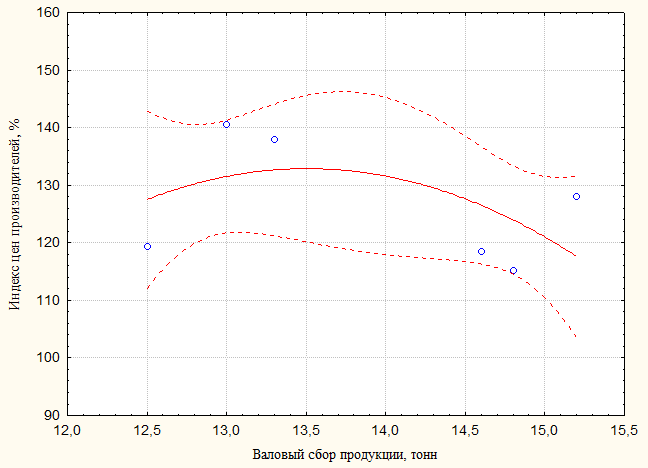
Рисунок 6.2 - Вид диаграммы рассеяния с доверительной
|
|
|
областью при доверительной вероятности в 75% для степенной модели
Вывод: в доверительную область для квадратичного уравнения регрессии для описания зависимости между валовым сбором овощей и индексом цен на них входят все точки.
Оценка полученных результатов и их обобщение.
На основе проведенного анализа были получены следующие результаты:
– линейное уравнение y = 179,923 − 3,835∙x не является применимым для описания зависимости между валовым сбором овощей в хозяйствах всех категорий и индексом цен производителей, поскольку несмотря на то, что средняя относительная ошибка аппроксимации равна 6,85%, рассчитанные значения F-статистики и t-статистики не удовлетворяют табличным значениям (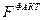
= 0,74183 << 
(1,4) = 7,71; –2,776 <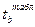 
<2,776, для нашего случая 
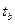= -0,861296);
– квадратичное уравнение y = -837,55 + 143,711∙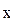 
− 5,3205∙ 
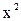является применимым для описания зависимости между валовым сбором овощей в хозяйствах всех категорий и индексом цен производителей, при этом средняя относительная ошибка аппроксимации составила 0,066007 (6,6%) и индекс корреляции равен 0,51;
– степенное уравнение y = 364,823∙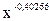 
является применимым для описания зависимости между валовым сбором овощей в хозяйствах всех категорий и индексом цен производителей, при этом средняя относительная ошибка аппроксимации составила 0,068676 (6,86 %) и индекс корреляции равен 0,38.
Таким образом, можно сделать вывод о том, что из предложенных трех моделей зависимости валового сбора овощей и индекса цен производителей наиболее оптимальной является квадратичная модель (0,066007 < 0,068676).
Заключение
В ходе лабораторной работы была выполнена спецификация исследуемой зависимости графическим способом. Было построено поле корреляции и выдвинута гипотеза о форме связи.
По условию задания необходимо было построить три модели для описания зависимости между валовым сбором овощей всех хозяйств и индексом цен производителей: линейную, квадратичную и степенную, что и было сделано с помощью метода наименьших квадратов (МНК). На графиках показаны все теоретические значения по каждой из моделей, для линейной и квадратичной модели построены доверительные области.
|
|
|
Следующим шагом была оценка адекватности построенных моделей. Для линейной регрессии проведена F – статистика и t – статистика, а также рассчитана средняя относительная ошибка аппроксимации. Результаты F – статистики и t – статистики оказались неудовлетворяющими условиям, и в связи с этим нам пришлось отвергнуть данную модель. Расчет средней относительной ошибки аппроксимации для квадратичной и степенной регрессий показал, что обе модели применимы для описания исходной зависимости. Поскольку 0,066007(
) < 0,068676(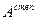
), то можно сделать вывод о том, что квадратичная модель лучше отражает исходную зависимость между валовым сбором овощей и индексом цен производителей.
|
|
|
