 |
Определение надежности моделей и адекватности построенных регрессий
|
|
|
|
Анализ линейного уравнения регрессии
Выдвинем гипотезу о том, что предсказания по регрессии дает меньшую погрешность, чем предсказания по среднему значению функции отклика.
Итоги анализа представлены в таблице 4.1.
Таблица 4.1.1 – Результаты регрессионного анализа парной линейной зависимости
| N = 6 | Итоги регрессии для зависимой переменной: Индекс цен производителя R=,39553006 R2=,15644403 Скорректир. R2= ----- F(1,4)=,74183 p<,43764 Станд. ошибка оценки: 11,015 | |||||
| Бета | Станд.ошиб. Бета | В | Станд. ошиб. В | t(4) | p-уровень | |
| Свободный член | 179,9227 | 62,05364 | 2,899471 | 0,044141 | ||
| Валовый сбор овощей | -0,395530 | 0,459227 | -3,8350 | 4,45255 | -0,861296 | 0,437644 |
Результаты следующие:
– R2 – коэффициент детерминации = 0,15644403;
– F(1,4) = 0,74183;
– t(4) – рассчитанные значения t-статистики = 2,899471 для свободного члена и - 0,861296 для независимой переменной;
– Станд. ошибка оценки (остаточная сумма квадратов) = 11,015.
Для определения средней относительной ошибки аппроксимации выполним дополнительные расчеты в основной таблице исходных данных.
Таблица 4.1.2 - Исходные данные после добавления столбцов
| Индекс цен производителей | Валовый сбор овощей | Теоретические | Погрешность | |
| 119,4 | 12,5 | 131,9855 | 0,105406198 | |
| 13,3 | 128,9175 | 0,0658152174 | ||
| 140,6 | 130,068 | 0,0749075391 | ||
| 115,2 | 14,8 | 123,165 | 0,069140625 | |
| 118,5 | 14,6 | 123,932 | 0,0458396624 | |
| 15,2 | 121,631 | 0,0497578125 |
Оценка линейного уравнения регрессии показала:
1) 
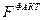= 0,74183 и имеет уровень 0,437644. 
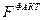(1,4) = 7,71, и для нашего случая << ,следовательно, есть основания для опровержения гипотезы;
2) для параметра b получили уровень значимости 0,437644. Это позволяет утверждать, что параметр b значимо отличается от 0. Но |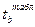 
| > 2,776. Для нашего примера 
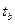= -0,861296, а это значит, что | 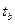| << | 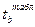|, и есть основания для отвергания гипотезы;
|
|
|
3) средняя ошибка составляет 0,68478 или 6,85%, что является допустимым.
Таблица 4.1.3 – Результаты расчета среднего значения для ошибки
| Переменная | Описательные статистики (Таблица данных) |
| Среднее значение | |
| Погрешность (линейная) | 0,068478 |
Вывод: линейное уравнение y = 179,923 − 3,835∙x не является применимым для описания зависимости между валовым сбором овощей в хозяйствах всех категорий и индексом цен производителей.
Анализ квадратичного уравнения регрессии
Для определения средней относительной ошибки аппроксимации выполним дополнительные расчеты в основной таблице исходных данных.
Таблица 4.2.1 - Исходные данные после добавления столбцов
| Индекс цен производителей | Валовый сбор овощей | Теоретические | Погрешность | |
| 119,4 | 12,5 | 127,509375 | 0,0679177136 | |
| 13,3 | 132,663055 | 0,0386735145 | ||
| 140,6 | 131,5285 | 0,0645199147 | ||
| 115,2 | 14,8 | 123,97048 | 0,0761326389 | |
| 118,5 | 14,6 | 126,51282 | 0,0676187342 | |
| 15,2 | 117,60888 | 0,081180625 |
Таким образом, оценка квадратичного уравнения регрессии показала: средняя ошибка аппроксимации составляет 0,066007 или 6,6 %, что является допустимым.
Таблица 4.2.2 - Результаты расчета среднего значения для ошибки
| Переменная | Описательные статистики (Данные квадратичной) |
| Среднее значение | |
| Погрешность (квадратичная) | 0,066007 |
Таблица 4.2.3 - Результаты оценки квадратичной регрессии
| Moдель: v1=a+b*v2+c*v2^2 (Данные квадратической in Workbook1) Зав.Пер.: Индекс цен производителей Уровень значимости: 95.0% (alpha=0.050) | ||||||
| Оценка | Станд. Ошибка | t-знач. сс = 3 | p - уровень | Ниж. Дов. Предел | Вер.Дов. Предел | |
| a | -837,555 | 1570,192 | -0,533409 | 0,630739 | -5834,61 | 4159,497 |
| b | 143,711 | 227,538 | 0,631589 | 0,572500 | -580,42 | 867,839 |
| c | -5,321 | 8,203 | -0,648588 | 0,562826 | -31,43 | 20,786 |
Вывод: квадратичное уравнение y = -837,55 + 143,711∙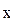 
− 5,3205∙ 
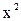является применимым для описания зависимости между валовым сбором овощей в хозяйствах всех категорий и индексом цен производителей.
|
|
|
Анализ степенного уравнения регрессии
Для определения средней относительной ошибки аппроксимации выполним дополнительные расчеты в основной таблице исходных данных.
Таблица 4.3.1 - Исходные данные для степенной модели после добавления столбцов
| Индекс цен производителей | Валовый сбор овощей | Теоретические | Погрешность | |
| 119,4 | 12,5 | 131,947275 | 0,959945735 | |
| 13,3 | 128,692165 | 0,964295263 | ||
| 140,6 | 129,879851 | 0,964822767 | ||
| 115,2 | 14,8 | 123,272053 | 0,95879627 | |
| 118,5 | 14,6 | 123,949246 | 0,959705376 | |
| 15,2 | 121,95541 | 0,962093514 |
Таблица 4.3.2 - Результаты расчета среднего значения для ошибки
| Переменная | Описательные статистики (Данные степенной регрессии) |
| Среднее значение | |
| Погрешность (степенная) | 0,068676 |
Таким образом, оценка степенного уравнения регрессии показала: средняя ошибка составляет 0,068676 или 6,86 %, что является допустимым.
Таблица 4.3.3 - Результаты оценки степенной регрессии
| Модель: v1=a*v2^b (Данные Степенной in Workbook1) Зав.Пер.: Индекс цен производителей Уровень значимости: 95.0% (alpha=0.050) | ||||||
| Оценка | Станд. Ошибка | t-знач. сс = 3 | p - уровень | Ниж. Дов. Предел | Вер.Дов. Предел | |
| a | 364,8233 | 467,3165 | 0,780677 | 0,478610 | -932,655 | 1662,302 |
| b | -0,4027 | 0,4878 | -0,825425 | 0,455514 | -1,757 | 0,952 |
Вывод: степенное уравнение y = 364,823∙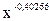 
является применимым для описания зависимости между валовым сбором овощей в хозяйствах всех категорий и индексом цен производителей.
|
|
|
