 |
Теория вероятностей и математическая статистика
|
|
|
|
1. Малинковский, Ю.В. Теория вероятностей и математическая статистика (часть 1. Теория вероятностей): Учебное пособие / Ю.В. Малинковский. – Гомель: УО «ГГУ им.Ф.Скорины», 2004. – 355 с.
2. Малинковский, Ю.В. Теория вероятностей и математическая статистика (часть 2. Математическая статистика): Учебное пособие / Ю.В. Малинковский. – Гомель: УО «ГГУ им.Ф.Скорины», 2004. – 146 с.
3. Севастьянов, Б.А. Курс теории вероятностей и математической статистики / Б.А. Севастьянов. – М.: Наука, 1980. – 256 с.
4. Ширяев, А.Н. Вероятность / А.Н. Ширяев. – М., 1980. – 576 с.
5. Севастьянов, Б.А. Сборник задач по теории вероятностей / Б.А. Севастьянов, В.П. Чистяков, А.М. Зубков. – М.: Наука, 1980. – 276 с.
6. Прохоров, А.В. Задачи по теории вероятностей / А.В. Прохоров, В.Г. Ушаков, Н.Г. Ушаков. – М.: Наука, – 1986. – 328 с.
7. Крамер, Г. Математические методы статистики. – М.: Мир, 1975. – 464 с.
8. Боровков, А.А. Курс теории вероятностей / А.А. Боровков. – М.: Наука, 1976. – 432 с.
9. Ширяев, А.Н. Вероятность / А.Н. Ширяев. – М., 1980. – 576 с.
Методы финансово-экономического управления
1. Кирлица, В.П. Финансовая математика: руководство к решению задач / В.П. Кирлица.- Мн.: ТетраСистемс, 2005.
2. Мелкумов, Я.С. Финансовые вычисления. Теория и практика: учебно-справочное пособие / Я.С.Мелкумов. – М.: «Филинъ», 1998.
3. Медведев, Г.А. Математические модели финансовых рисков. Риски страхования. / Г.А. Медведев / Ч. 2. Мн.: БГУ. – 2001. – 278 с.
4. Ротарь, В.И. Введение в математическую теорию страхования. / В.И. Ротарь, В.Е. Бенинг/ Обозрение прикладной и промышленной математики. 1994. – Т.1. – вып. 5. – С. 698 – 779.
5. Gerber H. An Introduction to Mathematical Risk Theory. Homewood: Irwin Inc. – 1979. – 285 c.
6. Гальперин, В.М. Макроэкономика / В.М. Гальперин. – СПб.: изд-во Санкт-Петербургского университета экономики и финансов, 1997.
|
|
|
7. Гальперин, В.М. Микроэкономика / В.М. Гальперин. – СПб.: изд-во Санкт-Петербургского университета экономики и финансов, 1998.
8. Замков, О.О. Математические методы в экономике / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. – М.: ДИС, 1997. – 368 с.
9. Мэнкью, Н.Г. Макроэкономика / Н.Г. Мэнкью. – М.: изд-во Моск. ун-та, 1994.
10. Елисеева, И.И. Эконометрика: учебное пособие / И.И.Елисеева.- М.: Финансы и статистика, 2004.
11. Харин, Ю.С. Эконометрическое моделирование: учебное пособие / В.И.Харин [.и др.]. – Мн.: БГУ, 2003.
12. Кирлица, В.П. Финансовая математика: руководство к решению задач / В.П. Кирлица.- Мн.: ТетраСистемс, 2005.
13. Мелкумов, Я.С. Финансовые вычисления. Теория и практика: учебно-справочное пособие / Я.С.Мелкумов. – М.: «Филинъ», 1998.
ПЕРЕЧЕНЬ ЗАДАЧ
Математический анализ
1. Найти пределы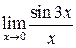 
; 
.
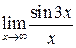2. Является ли функция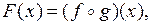 
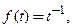
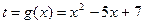непрерывной на 
? Дифференцируемой на ? Найти ее производную в тех точках, где она существует.
3. Проведя исследование, построить график функции 
.
4. Вычислить следующий интеграл: 
.
5. Найти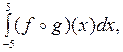 
где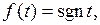 
6. Вычислить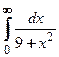 
.
7. Найти площадь фигуры, ограниченной кривыми y = 2 x - x 2, x + y = 0.
8. Найти: 
.
9. Исследовать на сходимость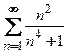 
.
10. Исследовать ряд на сходимость
.
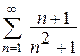11. Исследовать на сходимость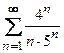 
.
12. Написать ряд Фурье функции 
на отрезке 
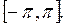
13. Найти области сходимости функционального ряда и его сумму. Исследовать сумму ряда на непрерывность
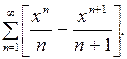
14. Найти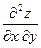 
, если 
15. Найти дифференциал d2u, если u = x 3 + y 3 + xy (x - y)
16. Изменить порядок интегрирования в следующем повторном интеграле
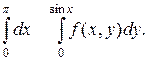
17. Вычислить 
, где точка О имеет координаты (0;0), а точка А – координаты (1;1), по следующим кривым:
а) ОА - отрезок прямой линии;
б) ОА - парабола, ось которой есть OY;
в) ОА - ломаная линия, состоящая из отрезка ОВ, оси ОХ и отрезка ВА, параллельного оси OY.
|
|
|
18. Применяя формулу Грина, вычислить следующий криволинейный интеграл:
, где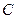 
- окружность с уравнением x 2 + y 2 = 4.
19. Вычислить предел: 
.
20. Существуют ли такие a и b, при которых функция
всюду непрерывна? Всюду дифференцируема?
21. Вычислить интеграл: 
.
22. Вычислить интеграл: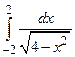 
.
23. Вычислить двойной интеграл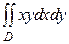 
, где область 
ограничена кривыми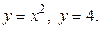 
24. Вычислить двойной интеграл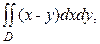 
где область ограничена линиями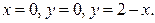 
25. Вычислить двойной интеграл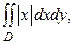 
где область есть круг с границей 
.
26. Найти изолированные особые точки функции
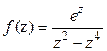
и выяснить их характер.
27. Найдите все значения суммы 
.
28. Вычислите вычет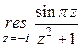 
.
29. Вычислите вычет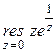 
.
30. Вычислите интеграл 
.
|
|
|
