 |
Методы финансово-экономического управления
|
|
|
|
1. Портфель состоит из трех одинаковых договоров страхования жизни. Страховая сумма при смерти от несчастного случая b 1=300 000 руб., а при смерти от естественных причин b 2=150 000 руб. Для каждого из застрахованных вероятность смерти от несчастного случая q 1=0,2, а от естественных причин q 2=0,1. Найти распределение суммарных выплат.
2. Портфель состоит из двух одинаковых договоров страхования жизни. Страховая сумма при смерти от несчастного случая b 1=300 000 руб., а при смерти от естественных причин b 2=150 000 руб. Для каждого из застрахованных вероятность смерти от несчастного случая q 1=0,2, а от естественных причин q 2=0,1. Найти распределение суммарных выплат.
3. Страховая компания заключила договор группового страхования N =5 000 человек сроком на 1 год. Вероятность смерти в течение года равна q =0,02. В случае смерти застрахованного компания выплачивает сумму b =350 000 руб. и ничего не платит в противном случае. Определить суммарную премию, достаточную, чтобы обеспечить вероятность разорения порядка 5%. (значение квантиля х95%=1,645).
4. Страховая компания заключила договор группового страхования N =10 000 человек сроком на 1 год. Вероятность смерти в течение года равна q =0,01. В случае смерти застрахованного компания выплачивает сумму b =500 000 руб. и ничего не платит в противном случае. Определить суммарную премию, достаточную, чтобы обеспечить вероятность разорения порядка 5%. (значение квантиля х95%=1,645).
5. Портфель страхования может порождать 0, 1 или 2 иска в заданном периоде времени с вероятностями 0,5, 0,2 и 0,3 соответственно. Размер индивидуального риска принимает значения 1 или 2 с вероятностями 0,5 и 0,5 соответственно. Найти распределение вероятностей совокупного иска.
|
|
|
6. Портфель страхования может порождать 0, 1 или 2 иска в заданном периоде времени с вероятностями 0,2, 0,4 и 0,4 соответственно. Размер индивидуального риска принимает значения 1 или 2 с вероятностями 0,2 и 0,8 соответственно. Найти распределение вероятностей совокупного иска.
7. При бюджете 120 д.е. и ценах факторов производства 
=2 и 
=5 фирма работает по технологии, отображаемой функцией 
. При каких объёмах труда и капитала объём выпуска фирмы будет максимальным?
8. Решить задачу потребительского выбора, найдя функции спроса, при ценах 
, 
и доходе 
со следующей функцией полезности 
. Изобразить допустимое множество и кривые безразличия.
9. Функция предельных издержек фирмы-монополиста МС=2+0,4Q. Функция спроса P =14 – 0,2Q. Найти оптимальный объем производства.
10. Даны функция общих издержек 
и функция спроса P=10. Найти прибыль для фирмы.
11. Фирма работает по технологии, отображаемой производственной функцией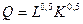 
. Цена труда – 8 д.е., цена капитала – 16 д.е. Определить среднюю производительность труда при нахождении фирмы в состоянии равновесия.
12. Функции спроса и предложения заданы следующим образом:
, 
.
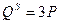Найти значение эластичности функций спроса и предложения в равновесной точке.
13. По статистическим данным об объемах продаж Y (тыс. ден. ед.), затратах на рекламу одной фирмы x 1 (тыс. ден. ед.), и индексе потребительских расходов за ряд текущих лет x 2 (%) проведен регрессионный анализ в MS Excel. Результаты анализа представлены на рисунке.
Построить уравнение линейной множественной регрессии и оценить его качество.
14. Для регрессионной модели зависимости цены квартиры y (тыс. ден. ед.) от расстояния от центра города x 1 (км), полезной площади x 2(кв. м) и числа этажей в доме x 3 (ед.) получено уравнение
y = 21,1 – 6,2 x 1 + 0,95 x 2 + 3,57 x 3.
Как измениться цена квартиры, если: а) расстояния от города увеличиться на 1 км, б) полезная площадь уменьшиться на 1 м2.
|
|
|
15. При исследовании зависимости оборота розничной торговли Y (млрд. руб.) от трех факторов: Х1 – денежные доходы населения (млрд. руб.); Х2 – численность безработных (млн. чел.); Х3 – официальный курс рубля по отношению к доллару США (руб./дол.) получена следующая модель:
Y = 55,74 + 0,33 X 1 – 4,98 X 2 + 2,38 X 3.
(–3,08) (9,74) (1,52) (8,37)
В скобках указаны расчетные значения t -критерия Стьюдента для коэффициентов уравнения. Значение коэффициента детерминации составляет
R 2 = 0,746, F = 14,25. При уровне значимости α = 0,05 табличные значения равны tтабл= 2,07, F табл = 3,35. Проведите анализ полученных результатов.
16. Имеются данные о ежемесячных объемах выпуска продукции (тыс. штук) предприятия. На рисунке представлены графики автокорреляционной (АКФ) и частной автокорреляционной (ЧАКФ) функций.
График АКФ
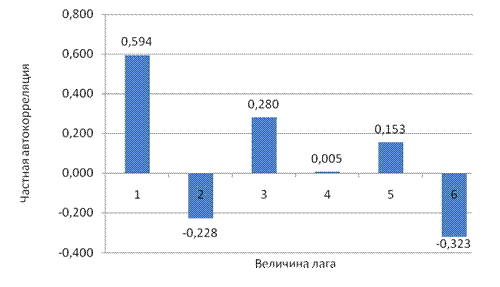
График ЧАКФ
Провести анализ структуры временного ряда.
17. Необходимо выбрать более выгодный вариант вклада под сложные проценты:
Вариант 1. Срок 3лет, 10 % годовых при начислении процентов 4 раза в год.
Вариант 2. Срок 2года под 8% годовых, если начисление процентов происходит каждый месяц.
18. Срочный вклад на сумму 100рублей заключен на 2 года по ставке сложных процентов 15 % годовых. Среднегодовой тем инфляции за этот период составил 10%. Определите наращенную сумму и реальную доходность финансовой операции, если банк начисляет сложные проценты ежемесячно.
19. Кредитв размере 1000 рублей необходимо погасить за 3 года, платежи в конце года. Процентная ставка по кредиту 20% годовых. Составить план погашения задолженности, используя аннуитетную схему.
20. Кредитв размере 10 млн. руб. необходимо погасить за 3 года, платежи в конце года. Процентная ставка по кредиту 20% годовых. Составить план погашения, используя дифференцированную схему.
|
|
|
