 |
Применение теории массового обслуживания в экономике
|
|
|
|
1. Буриков, А.Д. Теория массового обслуживания. Учебное пособие по спецкурсу /, А.Д. Буриков, Ю.В. Малинковский, М.А. Маталыцкий. – Гродно: ГрГУ. – 1984. – 106 с.
2. Гнеденко, Б.В. Введение в теорию массового обслуживания / Б.В. Гнеденко, И.Н. Коваленко. – М.: Изд-во ЛКИ, 2011. – 400 с.
3. Кремер, Н.Ш. Исследование операций в экономике: Учеб. пособие для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин. – М.: ЮНИТИ. – 2003. –407 с.
4. Фомин, Г.П. Математические методы и модели в коммерческой деятельности: Учебник / Г.П. Фомин. – М.: Финансы и статистика. – 2005. – 616 с.
5. Шелобаев, С.И. Математические методы и модели в экономике, финансах, бизнесе: Учеб. пособие для вузов / С.И. Шелобаев. – М.: ЮНИТИ-ДАНА. – 2001. – 367 с.
Экономика предприятия
1. Трудовой кодекс Республики Беларусь: одобрен Советом Республики 30 июня 1999г. (в ред.закона Республики Беларусь от 24 декабря 2007г., № 299-3) // Национальный реестр правовых актов Республики Беларусь. – 2008. – № 3, 2/1396.
2. Основные положения по составу затрат, включаемых в себестоимость продукции (работ, услуг): Постановление Минэкономики, Минфина, Минстатистики и анализа, Минтруда от 4.07.2002г., № 142/95/60/95.
3. Единая тарифная сетка работников производственных отраслей экономики Республики Беларусь. – Мн., 2000.
4. Головачев, А.С. Экономика предприятия: учебное пособие / А.С. Головачев. – Мн. – в 2-х ч., ч.1 – 2007г., ч.2 – 2008г.
5. Экономика предприятия (фирмы): учебное пособие / под ред. О.И. Волкова, О.В. Девяткина. – 3-е изд., перераб. и доп. – М., 2007.
6. Экономика предприятия: учебное пособие / под общ. ред. А.И.Ильина. – 3-е изд., перераб. и доп. – Мн., 2005.
7. Бабук, И.М. Экономика предприятия / И.М.Бабук. – Мн.,2006.
8. Экономика предприятия: учебное пособие / под общ. ред. Л.Н. Нехорошевой. – Мн., 2005.
|
|
|
9. Экономика, организация и планирование промышленного производства: учебное пособие / под общ. ред. Т.В.Карпей. – 4-е изд., испр. и доп. – Мн., 2004.
ПЕРЕЧЕНЬ ЗАДАЧ
Математический анализ
1. Найти пределы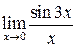 
; 
.
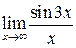2. Является ли функция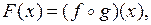 
непрерывной на 
? Дифференцируемой на 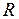? Найти ее производную в тех точках, где она существует.
3. Проведя исследование, построить график функции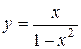 
.
4. Вычислить следующий интеграл: 
.
5. Найти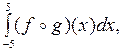 
где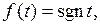 
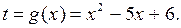
6. Вычислить 
.
7. Найти площадь фигуры, ограниченной кривыми y = 2 x - x 2, x + y = 0.
8. Найти: 
.
9. Исследовать на сходимость 
.
10. Исследовать ряд на сходимость
.
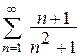11. Исследовать на сходимость 
.
12. Написать ряд Фурье функции 
на отрезке 
13. Найти области сходимости функционального ряда и его сумму. Исследовать сумму ряда на непрерывность
14. Найти 
, если 
15. Найти дифференциал d2u, если u = x 3 + y 3 + xy (x - y)
16. Изменить порядок интегрирования в следующем повторном интеграле
17. Вычислить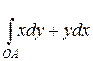 
, где точка О имеет координаты (0;0), а точка А – координаты (1;1), по следующим кривым:
а) ОА - отрезок прямой линии;
б) ОА - парабола, ось которой есть OY;
в) ОА - ломаная линия, состоящая из отрезка ОВ, оси ОХ и отрезка ВА, параллельного оси OY.
18. Применяя формулу Грина, вычислить следующий криволинейный интеграл:
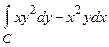, где 
- окружность с уравнением x 2 + y 2 = 4.
19. Вычислить предел: 
.
20. Существуют ли такие a и b, при которых функция
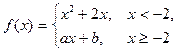
всюду непрерывна? Всюду дифференцируема?
Геометрия и алгебра
1. Решите матричное уравнение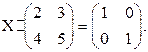 
2. Пользуясь схемой Горнера, вычислите 
, если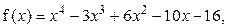 
3. Найдите разложение вектора 
по векторам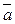 
и 
в пространстве 
:
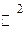4. Докажите, что фигура, ограниченная прямыми:
квадрат. Вычислите его площадь.
5. Найдите точку, симметричную точке 
относительно прямой 
|
|
|
на плоскости.
6. Докажите, что векторы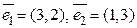 
образуют базис пространства 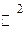. Найдите координаты вектора 
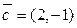в этом базисе.
7. В векторном пространстве 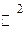найдите матрицу перехода от базиса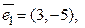 
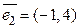к базису 
8. Решите систему линейных уравнений методом Гаусса
9. Линейный оператор 
в базисе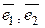 
имеет матрицу 
Найдите матрицу оператора в базисе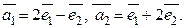 
10. Докажите, что в евклидовом пространстве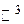 
векторы 
и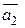 
ортогональны. Дополните систему векторов 
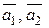до ортогонального базиса пространства :
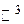11. Найдите базис ядра линейного оператора векторного пространства 
, заданного в некотором базисе 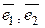матрицей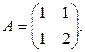 
12. Найдите расстояние между параллельными плоскостям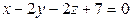и
и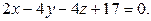 
13. Найдите проекцию точки 
на плоскость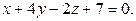 
|
|
|
