 |
Теория вероятностей и математическая статистика
|
|
|
|
1. В ящике имеется 6 деталей, среди которых 2 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятности того, что среди извлеченных деталей: а) ровно одна окрашена; б) хотя бы одна окрашена.
2. На отрезок АВ длины 5 наудачу брошено четыре точек. Найти вероятность того, три точки будут находиться от точки А на расстоянии, меньшем 2, а одна – на расстоянии, большем 2.
3. На отрезке длины 6 наудачу выбирают две точки. Найти вероятность того, что сумма расстояний от этих точек до правого конца отрезка превзойдет 2.
4. Игральная кость подбрасывается три раза. Случайная величина ξ – количество выпадений тройки. Найти ряд распределения и функцию распределения случайной величины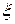 
.
5. Задана плотность распределения вероятностей случайной величины 
:
.
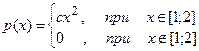Найти постоянный параметр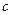 
, математическое ожидание случайной величины .
6. Пусть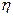 
– случайная величина, имеющая показательное распределение с параметром 5, 
, 
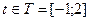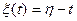. Построить реализации случайного процесса 
. Найти конечномерные распределения.
Математическая теория финансовых рисков
1. Портфель состоит из трех одинаковых договоров страхования жизни. Страховая сумма при смерти от несчастного случая b 1=300 000 руб., а при смерти от естественных причин b 2=150 000 руб. Для каждого из застрахованных вероятность смерти от несчастного случая q 1=0,2, а от естественных причин q 2=0,1. Найти распределение суммарных выплат.
2. Портфель состоит из двух одинаковых договоров страхования жизни. Страховая сумма при смерти от несчастного случая b 1=300 000 руб., а при смерти от естественных причин b 2=150 000 руб. Для каждого из застрахованных вероятность смерти от несчастного случая q 1=0,2, а от естественных причин q 2=0,1. Найти распределение суммарных выплат.
|
|
|
3. Страховая компания заключила договор группового страхования N =5 000 человек сроком на 1 год. Вероятность смерти в течение года равна q =0,02. В случае смерти застрахованного компания выплачивает сумму b =350 000 руб. и ничего не платит в противном случае. Определить суммарную премию, достаточную, чтобы обеспечить вероятность разорения порядка 5%. (значение квантиля х95%=1,645).
4. Страховая компания заключила договор группового страхования N =10 000 человек сроком на 1 год. Вероятность смерти в течение года равна q =0,01. В случае смерти застрахованного компания выплачивает сумму b =500 000 руб. и ничего не платит в противном случае. Определить суммарную премию, достаточную, чтобы обеспечить вероятность разорения порядка 5%. (значение квантиля х95%=1,645).
5. Портфель страхования может порождать 0, 1 или 2 иска в заданном периоде времени с вероятностями 0,5, 0,2 и 0,3 соответственно. Размер индивидуального риска принимает значения 1 или 2 с вероятностями 0,5 и 0,5 соответственно. Найти распределение вероятностей совокупного иска.
6. Портфель страхования может порождать 0, 1 или 2 иска в заданном периоде времени с вероятностями 0,2, 0,4 и 0,4 соответственно. Размер индивидуального риска принимает значения 1 или 2 с вероятностями 0,2 и 0,8 соответственно. Найти распределение вероятностей совокупного иска.
Методы оптимизации
1. Решить симплекс-методом
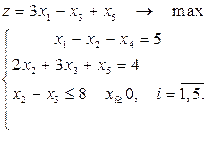
2. Исследовать задачу НЛП, используя правило множителей Лагранжа
z = x1+2x22 ® min
6x1 + x2 £ 4
x1 + 2x2 £ 6
3. Построить оптимальную по суммарному штрафу последовательность обслуживания заявок на одном приборе с данными
| N | |||||
| t(мин) время обслуживания | |||||
| с(руб) штраф за ожидание в очереди |
Исследование операций
1. Решить задачу о кратчайшем маршруте
|
|
|
2. Решить матричную игру геометрическим способом
|
|
|
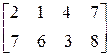
