 |
Радиальная составляющая вектора скорости
|
|
|
|
Вектор скорости представляется в виде суммы двух векторов, каждый из которых является составляющей скорости по направлению, задаваемому векторами r0 и p0 соответственно. Первое слагаемое называется радиальной составляющей, а второе - трансверсальной составляющей скорости точки: 
. Проекции скорости на радиальную и трансверсальную оси имею вид 
Формула Ривальса
По формуле Ривальса можно найти распределение ускорений, мгновенный центр ускорений, а так же вычислить ускорение центра мгновенного вращения (и скорость мгновенного центра ускорений). Вообще говоря, Ривальс – мутный чел какой-то. В англоязычной литературе эта формула вообще идет без названия, инфы о нем вообще нет.
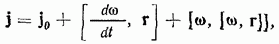Эта формула определяет абсолютные ускорения точек твердого тела.
Вектор ускорения точки при естественном способе задания движения.
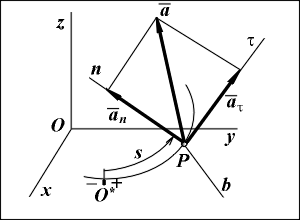Вектор ускорения 
точки лежит в соприкасающейся плоскости 
и определяется двумя проекциями 
и 
(
= 0):
- проекция ускорения точки на касательную равна первой производной от алгебраической скорости или второй производной от криволинейной координаты точки по времени:
или 
.
- проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой:
.
Величины и соответственно называют касательным и нормальным ускорениями точки.
Вектор ускорения является векторной суммой касательной составляющей , направленной вдоль касательной , и нормальной составляющей , направленной вдоль главной нормали 
: 
.
Так как эти составляющие взаимно перпендикулярны, то модуль вектора определяется по формуле: 
.
Чему равна производная от вектора постоянного по модуля по скалярному аргументу?
|
|
|
Производная постоянного по модулю вектора по скалярному аргументу есть вектор, перпендикулярный исходному.
Абсолютное пространство, абсолютное время.
Абсолютное пространство представляет собой трехмерное, однородное и изотропное неподвижное евклидово пространство.
Абсолютное время считается непрерывно изменяющейся величиной, оно течёт от прошлого к будущему. Время однородно, одинаково во всех точках пространства и не зависит от движения материи
Связь полярных и декартовых координат.
17. Движение тела может рассматриваться как результат сложения поступательного движения и вращения тела относительно одной из точек тела, называемой полюсом.
18. Трансверсальная составляющая ускорения точки
Ускорение точки: 
, где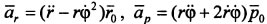 
- радиальная и трансверсальная составляющие ускорения точки соответственно. Так как составляющие ускорения взаимно перпендикулярны, то его модуль: 
.
19. С оставляющая же ускорения 
не отклонит тело от этой прямой, так как является осестремительным переносным ускорением и всегда направлена по этой прямой.
Таким образом, имеем:
Полученное равенство служит математическим выражением теоремы Кориолиса: Абсолютное ускорение точки в сложном движении равно геометрической сумме её переносного ускорения (сумма первых трёх слагаемых в правой части), относительного ускорения (четвёртое слагаемое) и добавочного кориолисова ускорения (последнее слагаемое), равного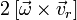 
.
Используя обозначения 
и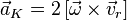 
, получим запись теоремы Кориолиса в более сжатом виде:
Переносное движение точки
Движение точки, обусловленное движением подвижной системы координат, называется переносным движением точки.
|
|
|
