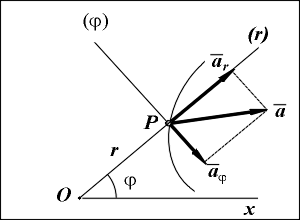
Радиальная составляющая вектора ускорения

Рассмотрим, как вычисляются скорость и ускорение точки при задании ее движения в полярных координатах, то есть когда заданы уравнения движения точки в виде r = r(t); 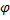= 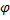(t).

Вектор ускорения a точки направлен в сторону вогнутости траектории и определяется своими проекциями a_r и 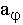на оси Pr и P 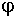по формулам:

a_r = d²r/dt² - r (d 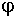/dt)² = - r ()²;

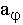= r (d² 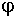/dt²) + 2 (dr/dt) (d 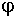/dt) = r 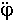+ 2 .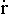

Величины a_r и 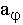соответственно называются радиальным и трансверсальным ускорениями точки.

Каким условием связаны проекции скоростей точек C и D на вектор DC

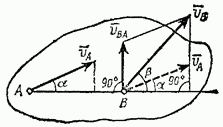
Проекции скоростей двух точен твердого тела на ось, проходящую через эти точки, равны друг другу, при этом 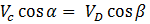(на рисунке точки А и В)

Абсолютное ускорение точки

Движение, совершаемое точкой по отношению к неподвижной системе отсчета O ₁ x ₁ y ₁ z ₁, называется абсолютным или сложным. Траектория этого движения называется абсолютной траекто­рией, скорость - абсолютной скоростью (обозначается ) и ускорение - абсолютным ускорением (обозначается 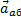). Равенство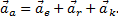

представляет теорему сложения ускорений в случае, когда переносное движение является произвольным: абсолютное ускорение точки равно векторной сумме переносного, относительного и поворотного ускоре­ний. Эту теорему часто называют теоремой Кориолиса.

 

24. Найти производную по времени от v×Ƭ¯ (тау) – единичный вектор касательной к траектории

Выражение для тангенциального ускорения можно найти, продифференцировав по времени вектор скорости, представленный в виде через единичный вектор касательной :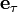

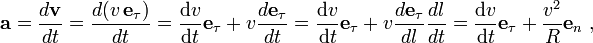
где первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение.

Здесь использовано обозначение 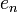для единичного вектора нормали к траектории и 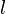- для текущей длины траектории (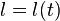); в последнем переходе также использовано очевидное

 

Естественный способ задания движения точки (что включает в себя)

1.1.3 Естественный способ задания движения точки

 

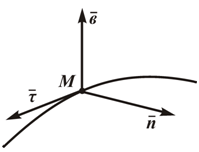
Рисунок 1.4

На рисунке 1.4:

τ - орт касательной;

n - орт нормали;

b - орт бинормали;

При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

 

Единичные орты τ, n, b определяют направление соответствующих осей в каждой точке кривой.

Рисунок 1.5

 

Чтобы задать закон движения точки естественным способом необходимо:

1) знать траекторию движения;

2) установить начало отсчета на этой кривой;

3) установить положительное направление движения;

4) дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t).

Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

 

 

 

Величины скоростей двух точек твердого тела в плоском движении в некоторый момент времени, пропорц. их расстоянию до третьей точки. Что это за точки?

26. Допустим, что так…

Мгновенным центром скоростей (МЦС) называется точка плоской фигуры, скорость которой в данный момент времени равна нулю (речь идет о плоскопараллельном движении твердого тела).

Для определения МЦС надо знать только направления скоростей VА и VВ каких-нибудь двух точек А и В сечения тела: МЦС находится в точке пересечения перпендикуляров, восстановленных из точек А и В к скоростям этих точек. Пусть Р – МЦС.

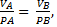то есть скорости точек тела пропорциональны их расстояниям до МЦС.

 

 

Формула Бура.

(получается из зависимости между полной и локальной производными): .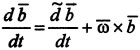

 

Что такое циклоида.

Цикло́ида (от греч. κυκλοειδής — круглый) — плоская трансцендентная кривая. Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса , катящейся без скольжения по прямой.

Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса .

· Циклоида описывается параметрически

,

.

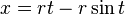· Уравнение в декартовых координатах:

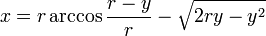
· Циклоида может быть получена как решение дифференциального уравнения:

 

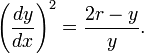
29 Ускорение Кориолиса

Ускорение Кориолиса или поворотное ускорение определяется по формуле

a_C = 2 ω_e * ν_r, где ω _e - переносная угловая скорость, ν_r - относительная скорость точки. Направление ускорения Кориолиса определяется по правилу векторного произведения или по правилу Жуковского. Величина ускорения Кориолиса определяется выражением a_C = 2 ω_e ν_r sinα,где α – угол между векторами ω_e и ν_r.

Ускорение Кориолиса с одной стороны характеризует изменение относительной скорости по направлению за счет переносного вращения и, с другой стороны, изменение величины переносной скорости за счет относительного движения.

30 Неподвижная центроида

ЦЕНТРОИДА - геом. место мгновенных центров вращения при движении неизменяемой плоской фигуры в её плоскости. На неподвижной плоскости это геом. место образует неподвижную Ц., а на плоскости, движущейся вместе с фигурой,- подвижную Ц. В каждый момент времени эти Ц. касаются друг друга в точке, являющейся для этого момента мгновенным центром вращения. Движение фигуры в её плоскости можно осуществить качением без скольжения подвижной Ц. по неподвижной.

31 НЦУ

31. МЦУ

При движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорение которой в этот момент равно нулю. Эту точку называют мгновенным центром ускорений (МЦУ). Для того чтобы определить МЦУ, необходимо к векторам ускорений двух различных точек тела провести прямые под равными углами 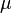. В точке пересечения проведённых прямых и будет находиться мгновенный центр ускорений. Угол 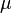должен удовлетворять равенству:

где

— угловое ускорение тела;

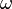— угловая скорость тела.

32 Нормальная составляющая вектора скорости точки

При движении тела по криволинейной траектории его скорость изменяется по модулю и направлению. Изменение вектора скорости за некоторый малый промежуток времени Δ t можно задать с помощью вектора 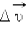(рис. 1.1.4).Вектор изменения скорости за малое время Δ t можно разложить на две составляющие: направленную вдоль вектора (касательная составляющая), и 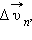направленную перпендикулярно вектору (нормальная составляющая).

Рисунок 1.1.4. Изменение вектора скорости по величине и направлению. 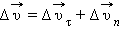– изменение вектора скорости за время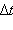

 

34?

 

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: