 |
Характеристика приемов введения понятий
|
|
|
|
Возможны следующие приёмы при введении понятий:
1) можно составить такие упражнения, которые позволяют учащимся быстро сформулировать определение нового понятия.
Например: а) Выписать несколько первых членов последовательности (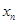 ), у которой
), у которой  =2,
=2,  . Такая последовательность называется геометрической прогрессией. Попытайтесь сформулировать её определение. Можно ограничиться подготовкой к восприятию нового понятия.
. Такая последовательность называется геометрической прогрессией. Попытайтесь сформулировать её определение. Можно ограничиться подготовкой к восприятию нового понятия.
б) Выписать несколько первых членов последовательности (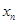 ), у которой
), у которой 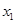 =4,
=4,  Далее учитель сообщает, что такая последовательность называется арифметической прогрессией и сам сообщает её определение.
Далее учитель сообщает, что такая последовательность называется арифметической прогрессией и сам сообщает её определение.
2) при изучении геометрических понятий упражнения формулируются таким образом, чтобы учащиеся построили сами необходимую фигуру и смогли выделить признаки нового понятия, необходимые для формулировки определения.
Например: постройте произвольный треугольник, соедините отрезком его вершину с серединой противоположной стороны. Такой отрезок называется медианой. Сформулируйте определение медианы.
Иногда предлагается составить модель либо, рассматривая готовые модели и чертежи, выделить признаки нового понятия и сформулировать его определение.
Например: введено в 10 классе определение параллелепипеда. По предложенным моделям наклонного, прямого и прямоугольного параллелепипедов выделить признаки, по которым эти понятия различаются. Сформулировать соответствующие определения прямого и прямоугольного параллелепипедов.
3) Многие алгебраические понятия вводятся на основании рассмотрения частных примеров.
Например: графиком линейной функции является прямая.
4) Метод целесообразных задач, (разработан С.И. Шохором-Троцким) С помощью специально подобранной задачи учащиеся приходят к выводу о необходимости введения нового понятия и целесообразности придания ему именно такого смысла, который оно уже имеет в математике.
|
|
|
В 5-6 классах таким методом вводятся понятия: уравнение, корень уравнения, решение неравенств, понятие действий сложения, вычитания, умножения, деления над натуральными числами, десятичными и обыкновенными дробями и т.д.
Конкретно-индуктивный метод
Сущность:
а) рассматриваются конкретные примеры;
б) выделяются существенные свойства;
в) формулируется определение;
г) выполняются упражнения: на распознавание; на конструирование;
д) работа над свойствами, не включёнными в определение;
е) применение свойств.
Например: тема – параллелограммы:

|

 а)
а)
 | |||||
 |  | ||||
1, 3, 5 – параллелограммы.
б) существенные признаки: четырёхугольник, попарная параллельность сторон.
в) распознавание, построение:
г) найти (построить) четвёртую вершину параллелограмма (* - задача №3, ст.96, Геометрия 7-11 класс: Сколько можно построить параллелограммов с вершинами в трёх заданных точках, не лежащих на одной прямой? Постройте их.).
д) другие свойства:
AC и BD пересекаются в точке О и АО=ОС, ВО=ОD; АВ=СD, AD=BC.
е) 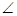 А=
А= 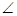 С,
С, 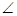 В=
В= 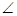 D.
D.

 B
B
AD
Закрепление: решение задач №4-23, стр.96-97, Геометрия 7-11, Погорелов.
Перспективное значение:
а) используется при изучении и определении прямоугольника и ромба;
б) принцип параллельности и равенства отрезков, заключённых между параллельными прямыми в теореме Фалеса;
в) понятие параллельного переноса (вектора);
г) свойство параллелограмма используется при выводе площади треугольника;
д) параллельность и перпендикулярность в пространстве; параллелепипед; призма.
|
|
|


