 |
Абстрактно-дедуктивный метод
|
|
|
|
Сущность:
а) определение понятия: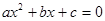 
- квадратное уравнение;
б) выделение существенных свойств: х – переменная; a, b, c – числа; а≠0 при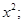 
в) конкретизация понятия: 
- приведенное; примеры уравнений 
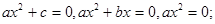
г) упражнения: на распознавание, на конструирование;
д) изучение свойств, не включённых в определение: корни уравнения и их свойства;
е) решение задач.
В школе абстрактно-дедуктивный способ применяется тогда, когда новое понятие полностью подготовлено изучением предыдущих понятий, в том числе изучением ближайшего родового понятия, а видовое отличие нового понятия весьма простое и понятное учащимся.
Например: определение ромба после изучения параллелограмма.
Кроме того, указанный метод используется:
1) при составлении “родословной” определения понятия:
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это параллелограмм, у которого все углы прямые.
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны.
Четырёхугольник – фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков.
Иначе говоря, родословная представляет собой цепочку понятий, построенных через обобщения предыдущего понятия, финалом которой является неопределяемое понятие (напомним, что в курсе школьной геометрии к таковым относятся точка, фигура, плоскость, расстояние (лежать между));
2) классификация;
3) применяется к доказательствам теорем и решению задач;
4) широко используется в процессе актуализации знаний.
Рассмотрим этот процесс, представленный системой задач:
а) Дан прямоугольный треугольник со сторонами 3см и 4см. Найти длину медианы, проведённой к гипотенузе.
|
|
|
б) Доказать, что медиана, проведённая из вершины прямого угла треугольника, равна половине гипотенузы.
в) Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, проведёнными к гипотенузе.
г) На продолжении наибольшей стороны АС треугольника АВС отложен отрезок СМ, равный стороне ВС. Доказать, что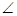 
АВМ тупой.
В большинстве случаев в школьном преподавании применяется конкретно-индуктивный способ. В частности, таким методом вводятся понятия в пропедевтических циклах начал алгебры и геометрии в 1-6 классах, причём многие определяющие понятия вводятся описательно, без строгих формулировок.
Незнание учителем различных методов введения определений приводит к формализму, который проявляется следующим образом:
а) учащиеся затрудняются применить определения в непривычной ситуации, хотя и помнят его формулировку.
Например: 1) считают функцию 
- чётной, т.к. “cos” – чётная;
2) 
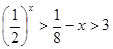- не понимают связь между монотонностью функции и решением неравенства, т.е. не могут применять соответствующие определения, в которых основной приём исследования состоит в оценке знака разности значений функции, т.е. в решении неравенства.
б) учащиеся обладают навыками решения задач какого-либо типа, но не могут объяснить, на основании каких определений, аксиом, теорем они выполняют те или иные преобразования.
Например: 1)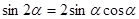 
- преобразовать согласно этой формуле 
и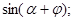 
2) представьте, что на столе – модель четырёхугольной пирамиды. Какой многоугольник будет основанием этой пирамиды, если модель положить на стол боковой гранью? (четырёхугольник).
Процесс формирования знаний, умений и навыков не ограничивается сообщением новых знаний.
Эти знания должны быть усвоены и закреплены.
|
|
|
