 |
Изучение вынужденных колебаний
|
|
|
|
Цель работы: изучить зависимость силы тока в электрической цепи переменного тока от частоты, познакомиться с явлением резонанса напряжений.
Оборудование: плата с электрической цепью из соединенных последовательно конденсатора, катушки индуктивности и резистора, генератор переменного тока, мультиметр.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Подключение электрической цепи к генератору переменного напряжения приводит к возникновению в цепи переменного электрического тока. Это ток, который изменяется по величине и по направлению. Переменный ток может рассматриваться как вынужденные колебания силы тока, заряда, в цепи под действием генератора.
| ○ ○ |
| Е ~ |
| Рис. 1 |
| L |
| C |
| R |
, где ω – циклическая частота генератора. Чтобы определить силу тока в цепи, применим закон Ома: сумма падений напряжения на конденсаторе 
, резисторе JR равна алгебраической сумме ЭДС генератора и ЭДС самоиндукции катушки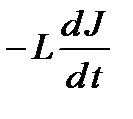 
. Здесь J – сила тока, q – заряд конденсатора. В итоге
. (1)
Перейдем в уравнении к одной переменной – к заряду, по соотношениям: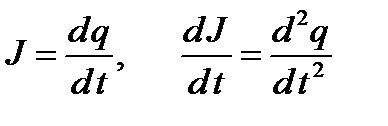 
. В результате получим уравнение
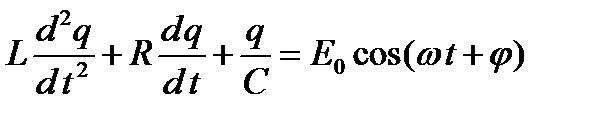. (2)
Это неоднородное дифференциальное уравнение второго порядка. Его решением является сумма общего решения однородного уравнения (это уравнение затухающих колебаний) и частного решения неоднородного уравнения (вынужденные колебания). Известно, что затухающие колебания со временем исчезают и остаются только вынужденные колебания с частотой генератора. Частное решение уравнения (2) будем искать в виде гармонической функции силы тока, так как обычно в электрической цепи измеряют силу тока, а не заряд:
|
|
|
J =J 0cos w t. (3)
Подставив функции для заряда в уравнение (2) по соотношениям: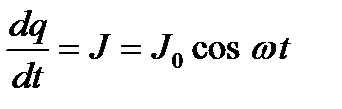 
; 
; 
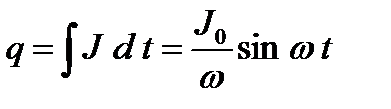, получим
. (4)
| j |
| J0(ωL-1/ωC) |
| Рис. 2 |
| J 0 R |
| E 0 |
| U |
| J 0 ωL |
| J 0 /ωC |
В уравнении (4) два неизвестных параметра: амплитуда силы тока J 0и сдвиг фаз между током и напряжением j. Для их определения воспользуемся геометрическим методом решения тригонометрических уравнений. Это метод векторных диаграмм. Проведем из полюса векторы, длины которых равны амплитудам уравнения (4), под углом к оси напряжений, равным начальным фазам (рис. 2). Если эти векторы поворачивать с угловой скоростью, равной циклической частоте колебаний, то проекции векторов на ось напряжений будут совпадать с членами уравнения (4).
. Откуда амплитуда силы тока
. (5)
Это закон Ома для цепи переменного тока. Знаменатель следует трактовать как полное сопротивление цепи Z
. (6)
Активное сопротивление R обусловлено сопротивлением движению электронов в проводнике. Ограничение силы тока противодействием ЭДС самоиндукции эквивалентно действию индуктивного сопротивления ωL. Ограничение тока процессами перезарядки конденсатора эквивалентно емкостному сопротивлению 1/(ωС). Сопротивления характеризуют способность превращать энергию источника тока в энергию магнитного поля катушки, в энергию электрического поля конденсатора и в теплоту на резисторе.
Амплитуда силы тока зависит не только от ЭДС, но и от частоты. При частоте ω = 0 (постоянное напряжение) тока в цепи нет, этому препятствует конденсатор. С увеличением частоты ток начинает возрастать по мере уменьшения емкостного сопротивления. Но растет индуктивное сопротивление. Поэтому сила тока, достигнув максимума в момент равенства индуктивного и емкостного сопротивлений 
, спадает при высоких частотах (рис. 3).
|
|
|
| J 0 |
| ω |
| Δ ω |
| J max |
| Jmax/ 2 |
| ωрез |
| Рис. 3 |
. При резонансе падения напряжения на катушке и на конденсаторе изменяются в противофазе и компенсируются. В этот момент полное сопротивление цепи равно только активному сопротивлению R. При малом сопротивлении сила тока при резонансе может достигать огромных значений J max =E 0 /R. Напряжения на конденсаторе и катушке будут тоже велики и могут во много раз превышать ЭДС генератора.
Если по уравнению (5) определить две частоты, при которых сила тока меньше максимального значения в 
раз, то разность частот окажется равной удвоенному значению коэффициента затухания: 
.
| Генератор |
| L |
| R |
| Плата |
| С |
| Рис. 4 |
| ○ |
| ○ |
| ○ |
| ○ |
| ○ |
| ○ |
| ○ |
| ○ |
| Мультиметр |
| ○ |
| ○ |
| Еген |
Экспериментальное изучение цепи переменного тока производится на лабораторной установке, состоящей из платы с электрической цепью, генератора и мультиметра для измерения напряжений на элементах цепи. (рис. 4).
ВЫПОЛНЕНИЕ РАБОТЫ
1. Подключить соединительными проводниками на плате выбранные резистор и конденсатор. Подключить генератор к клеммам платы Генератор, вход мультиметра к гнездам конденсатора.
Включить генератор и мультиметр в сеть 220 В.
2. Установить переключателями генератора режим синусоидального напряжения и диапазон частот 20 – 200 кГц. Проверьте, находится ли в этом диапазоне собственная частота цепи, 
.
Установить на мультиметре режим переменного напряжения U~, диапазон измерения 2 В. Если на индикаторе появится буква «П» (переполнение), то перейти на следующий диапазон.
3. Изменяя частоту генератора с интервалом 10 кГц, измерить мультиметром напряжение на выбранном элементе цепи (например, на конденсаторе). Убедиться, что резкое возрастание напряжения при резонансе обнаружено. Плавно изменяя частоту вблизи резонанса, определить максимальное показание мультиметра и частоту резонанса. Результаты записать в табл. 1.
|
|
|
Таблица 1
| Частота nген, Гц | |||||||||
| Амплитуда А, В |
4. Подсоединить поочередно в режиме резонанса соединительные проводники мультиметра к гнездам резистора R, катушки индуктивности L и конденсатора C и измерить на них падения напряжения. Подсоединить проводники к гнездам генератора и измерить ЭДС генератора Еген. Результаты измерений и параметры цепи записать в табл. 2.
Таблица 2
| ν, кГц | R, Ом | L, мГ | C, мкФ | UR, В | UL, В | UC , В | Eген,, В |
Убедиться, что при резонансе падения напряжения на конденсаторе и катушке индуктивности почти равны и намного больше ЭДС, что падение напряжения на резисторе почти равно ЭДС генератора.
Выключить приборы.
5. Построить график зависимости напряжения на конденсаторе от частоты. Размер графика не менее половины страницы. На осях координат указать равномерный масштаб. Около точек провести плавную линию.
6. Вычислить 
. Провести на графике линию с этой ординатой. Определить абсциссы точек пересечения с резонансной кривой. Найти по графику полуширину резонансной кривой (рис. 3).
7. Определить экспериментальное значение коэффициента затухания 
. Сравнить с теоретическим значением 
.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Запишите уравнение закона Ома для цепи переменного тока из соединенных последовательно резистора, конденсатора и катушки индуктивности.
2. Выведите дифференциальное уравнение закона Ома для электрического заряда. В каком виде находится решение уравнения?
3. Объясните метод векторных диаграмм при сложении напряжений на элементах цепи переменного тока. Получите уравнение закона Ома для цепи переменного тока.
4. Объясните физический смысл сопротивлений резистора, катушки и конденсатора переменному току. Как они зависят от частоты?
|
|
|
5. Объясните зависимость силы тока в цепи переменного тока от частоты генератора. Дайте определение резонанса. Чем опасен резонанс?
6. Объясните способ определения коэффициента затухания по резонансной кривой.
Работа 25 а
|
|
|
