 |
Вероятностные задачи теории надежности
|
|
|
|
Задание:
Определить вероятность повреждения энергоблока, представляющего собой последовательное соединение парового котла, паровой турбины и электрического генератора. Паровая турбина получает весь пар от котла. Генератор расположен на одном валу с турбиной, т.е. использует всю её мощность. Вероятность повреждения отдельных элементов: котла qK = 0.02; турбины qm = 0.01; генератора qr = 0.001.
Решение:
Энергоблок представляет из себя систему из трёх последовательно соединённых элементов, т.е. аварийный выход из работы хотя бы одного элемента приводит к отказу энергоблока.
Вероятности безотказной работы отдельных блоков составляют соответственно
Можно решить эту задачу анализом всех возможных сочетаний повреждения элементов блока. Всего их семь: 1) котла; 2) турбины; 3) генератора; 4) котла и турбины; 5) котла и генератора; 6) турбины и генератора; 7) котла, турбины и генератора.
При этом соответствующие вероятности отказа энергоблока в этих ситуациях составят:
q5, q6 и q7 практически равны 0.
Вероятность отказа энергоблока равна сумме вероятностей отказов элементов в этих семи ситуациях.
Задача может быть решена и более простым способом.
Вероятность безотказной работы энергоблока равна произведению вероятностей безотказной работы отдельных элементов:
Вероятность отказа:
Задание:
Топливо на котельную подается по двум ниткам трубопровода. По каждой из ниток котельная может получить 50 % топлива для ее нормальной работы. Вероятность выхода из строя одной нитки трубопровода составляет 0.05. Какова вероятность сохранения рабочего состояния котельной?
Решение:
Так как по каждой нитке трубопровода передается только половина необходимого количества топлива для нормальной работы котельной, отказ любой из двух ниток приводит к отказу работы котельной.
|
|
|
Вероятность выхода из строя хотя бы одной из двух ниток трубопровода составляет
Вторая нитка трубопровода выходит из строя с той же вероятностью.
Вероятность одновременного выхода ниток трубопровода из строя:
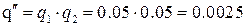
Вероятность отказа равна:
Вероятность сохранения рабочего состояния котельной составит
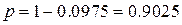
Задание:
В энергосистеме имеется группа из n однотипных котлов, работающих в одинаковых условиях. Вероятность исправного состояния котла - p, а неисправного q=1-p. Найти вероятность рабочего состояния m котлов из n.
m = 4; n = 5; p = 0.98; q = 1 - 0.98 = 0.02.
Решение:
Задача решается с применением схемы Бернулли.
Вероятность одновременного повреждения всех котлов - qn;
вероятность отказа всех котлов, кроме одного - npqn-1;
....................................................................................................
вероятность того, что в работе окажется m котлов изn - Cmn pm qn-m,
где Cmn= (n!)/[! (n-m)!] - число сочетаний из n элементов по n;
вероятность того, что в работе будут все котлы, кроме одного, - npn-1q;
вероятность того, что все котлы в рабочем состоянии - pn.
Сумма вероятностей всех возможных состояний соответствует разложению по биному Ньютона и равна единице.
Для числовых значений примера:
,
то есть вероятность рабочего состояния четырех котлов из 5 составляет 0.0923.
Задание:
Статистическая вероятность повреждения любой фазы трехфазной линии составляет 0.01. Если повреждение одной фазы произошло, то повреждение любой другой фазы имеет статистическую вероятность 0.2, третья фаза при условии повреждения двух других повреждается с вероятностью 0.5. Найти соотношение вероятностей одно-, двух- и трехфазных повреждений при условии, что авария начинается с повреждения одной фазы.
Решение:
Однофазные повреждения происходят с вероятностью 0.01 по условиям задачи. Вероятность двухфазных повреждений считается по формуле условной вероятности:
|
|
|
;
Вероятность трехфазных повреждений:
.
Таким образом, соотношение вероятностей одно-, двух- и трехфазных повреждений трехфазной линии составляет 0.01: 0.002: 0.001 или 10: 2: 1.
Задание:
Для сигнализации о перегреве обмотки турбогенератора установлены два независимых термосигнализатора, причем вероятность безотказной работы сигнализатора Р(А) = 0,9, сигнализатора Р(В) = 0,95. Определить вероятность срабатывания сигнализации при перегреве.
Решение:
События А и В (срабатывание сигнализаторов) независимы и совместны. Вероятность появления сигнала о перегреве составит
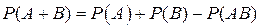
Задание:
Оператор устанавливает в узел машины четыре одинаковые детали. Узел будет работоспособен, если все четыре детали — стандартные. Имеется 50 деталей, причем априори известно, что пять из них нестандартные. Определить вероятность сборки работающего узла.
Решение:
Должны быть стандартны вес четыре устанавливаемые детали — логика И первая, И вторая и т.д. Вероятность появления последующей стандартной детали зависит от того, какой была установлена предыдущая деталь — стандартной или нестандартной. Следовательно, нужно воспользоваться теоремой умножения для зависимых событий:
Задание
Три группы станков (общее их число — 10) производят одни и те же детали, но качество деталей различно. Станки первой группы производят 94 % стандартных деталей, второй группы — 90 %, третьей — 85 %. Все детали отправлены на выборочный контроль. Определить вероятность того, что наудачу взятая деталь будет отвечать стандарту, если число станков первой группы равно пяти, второй — трем, третьей — двум.
Решение:
Событие А — проверенная деталь отвечает стандарту. Гипотезы: H1 — эта деталь станков первой группы, H2— второй, H3— третьей. Вероятность каждой гипотезы: Р(H1) = 0,5; Р(Н2) = 0,3; Р(H3) = 0,2. Условные вероятности при этих гипотезах: Р(А/Н1) = 0,94; Р(А/Н2) = 0,9; Р(А/Н3) = 0,85. Вероятность события А:
Задание
Два из трех независимо работающих элементов пускорегулирующей аппаратуры отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятность отказа первого, второго и третьего элементов соответственно равна 0,2; 0,4; 0,3.
|
|
|
Решение:
Обозначим А событие — отказали два элемента. Можно выдвинуть гипотезы: В1 — отказали первый и второй элементы, третий элемент исправен.
Тогда
В2 — отказали первый и третий элементы, второй элемент исправен.
Тогда
В3 — отказали второй и третий элементы, первый исправен, причем
(здесь 
, 
, 
), В4— отказал один элемент; В5 — отказали все три элемента; В6 — ни один из элементов не отказал. Вероятности последних трех гипотез не вычислены, так как при этих гипотезах событие А (отказали два элемента) невозможно.
Поскольку при гипотезах В1, B2, В3 событие А достоверно, то соответствующие условию вероятности равны единице:
Р(А/В1) = Р(А/В2) = Р(А/В3) = 1.
В соответствии с формулой полной вероятности
В соответствии с формулой Бейеса вероятность того, что отказали первый и второй элементы, равна:
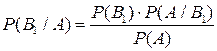
Задание:
В щеточном узле 10 щеток. Узел считается работоспособным, если пригодны не менее девяти щеток. Какова вероятность безотказной работы щеточного узла, если вероятность безотказной работы щетки за время / равна 0,9?
Решение.
Щеточный узел работоспособен, если работоспособны все 10 щеток из 10 — Р10 10 или девять щеток из 10 — Р9 10. Тогда в соответствии с (2.10) и теоремой сложения вероятностей
Задание:
Испытывается каждая из 15 секций машины. Вероятность того, что секция выдержит испытания, равна 0,9. Найти Наивероятнейшее число секций, которые выдержат испытания.
Решение.
По условию п = 15; р = 0,9; q = 0,1. В соответствии с
получим: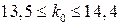 
. Отсюда k0 = 14.
Задание
Согласно методу «слабых узлов», синхронная машина представлена в виде трех узлов: контактные кольца (первый), подшипниковый узел (второй), обмотка якоря (третий). Вероятность безотказной работы в течение 1500 ч равна соответственно Р1 = 0,7; Р2 = 0,8; Р3 = 0,9. Проводятся испытания каждого узла на надежность. Найти вероятность того, что за 1500 ч будут работать безотказно: 1) все узлы; 2) два узла; 3) один узел; 4) ни один из узлов; 5) хотя бы один узел.
Решение.
|
|
|
Вероятности безотказной работы и вероятности отказов соответственно равны: Р1 = 0,7; Р2 = 0,8; Р3 = 0,9 и q1 = 0,3; q2 = 0,2; q3 = 0,1. Составим производящую функцию:
1. Вероятность того, что все три узла будут работать безотказно, равна коэффициенту при х3, т.е. Р3(3) = 0,504.
2. Вероятность того, что безотказно будут работать два узла (коэффициент при х2), Р2(3) = 0,398.
3. Вероятность того, что будет работать один узел, Р1 (3) = 0,092.
4. Вероятность того, что ни один из узлов не будет работать (коэффициент при х0 = 1, т.е. при свободном члене), равна Р0 (3) = 0,006.
5. Вероятность того, что будет работать хотя бы один узел — событие, противоположное событию, когда не работает ни одного узла. Значит, Р1.2.3 (3) = 1- Р0 (3) = 1 - 0,006=0.994
Показатели надежности
Задание
Определить коэффициент готовности и коэффициент простоя для трансформатора с ВН 35 кВ, для которого интенсивность отказов λ = 0,03 год-1, а время восстановления ТВ = 30 ч.
Решение
Средняя наработка до отказа:
Коэффициент готовности рассчитываем по формуле:
а коэффициент простоя – по выражению:
Задание
В течение года проводились наблюдения за группой однотипных водяных насосных установок. На основании записей в вахтовый журнал работы оборудования получены следующие показатели суммарной длительности режимов работы.
Режимы использования:
Режим нормальной работы (N) – 6860 ч.
Режим пуска (I) – 40 ч.
Режим регулирования (C) – 120 ч.
Режим останова (S) – 80 ч.
Режим технического обслуживания (M) – 50 ч.
Режимы простоя:
Режим планового и непланового предупредительного ремонта (R)–400 ч.
Режим простоя в работоспособном состоянии (O) – 100 ч.
Режим аварийного или нерасчётного воздействия (A) 50 ч.
Режим простоя в неработоспособном состоянии (F) – 300 ч.
режим восстановления после аварии (W) – 760 ч.
Вычислить оценки показателей надёжности по вариантам при условии, что число n (t) = 3 – простои в неработоспособном состоянии; n (t) = 3 – число восстановлений; n (t) = n (t) = n (t) = 1 (число циклов ТО, число ожиданий включения, число ремонтов).
Найти: коэффициенты планового применения, готовности, технического использования; среднее время наработки на отказ; время восстановления работоспособности; время восстановления функционирования; среднее время планового простоя; среднее время аварийного простоя; периодичность отказов, частоту отказов.
Решение
Коэффициент планового применения:
Коэффициент готовности:
Коэффициент технического использования:
Средняя наработка на отказ:
Среднее время восстановления работоспособности:
Среднее время восстановления функционирования:
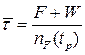
Среднее время планового простоя:
|
|
|
Периодичность отказов:
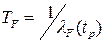
Частота отказов:
Задание
На испытания поставлено 100 электрических двигателей. В первом месяце отказало 15 двигателей, во втором — отказало 10 двигателей, в третьем — 10 двигателей; в четвертом — 8 двигателей; в пятом — 9 двигателей; в шестом — 7 двигателей, в седьмом — 1 1 двигателей, в восьмом — 12 двигателей; в девятом — 18 двигателей. В течение каждого месяца двигатели испытывались по 500 ч. Построить зависимость P(t), кумулятивную кривую, гистограмму, а также кривую жизни λ(t).
Решение.
Расчетные данные удобно оформить в виде табл. 3.1. Здесь первая колонка — номер месяца N; вторая — текущее время испытаний t; третья — интервал времени Δt; четвертая — количество двигателей, отказавших к концу каждого текущего месяца п(t); пятая — количество двигателей, отказавших в течение месяца n(Δt); шестая, седьмая, восьмая, девятая — соответственно показатели надежности P(t); Q(t); φ (t), 10-4 ч-1; λ (Δ t), 10-4 ч-1.
Расчеты проводятся в соответствии с формулами:
Вероятность безотказной работы:
Вероятность отказа:
Частота отказов:
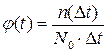
Интенсивность отказов:
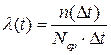
- среднее число изделий, исправно работающих в интервале Δt.
Ni, Ni+1– соответственно количество изделий, исправно работающих в начале и в конце интервала Δt.
Проведем расчет показателей надежности для первого месяца:
Аналогично проводятся расчеты для следующих месяцев.
Таблица
Данные к построению гистограмм
| Номер п/п | t | Δt | п(t) | n(Δt) | P(t) | Q(t) | φ (t), 10-4 ч-1 | λ (Δ t), 10-4 ч-1. |
| 0,85 | 0,15 | 3,0 | 3,24 | |||||
| 0,75 | 0,25 | 2,0 | 2,50 | |||||
| 0,65 | 0,35 | 2,0 | 2,86 | |||||
| 0,57 | 0,43 | 1,6 | 2,62 | |||||
| 0,48 | 0,52 | 1,8 | 3,43 | |||||
| 0,41 | 0,59 | 1,4 | 3,15 | |||||
| 0,30 | 0,70 | 2,2 | 6,57 | |||||
| 0,18 | 0,82 | 2,4 | 10,00 | |||||
| 0,00 | 1,00 | 3,6 | 40,00 |
«Кривая жизни» (1) и гистограмма (2)
«Кумулятивная кривая» (1) и кривая вероятности безотказной работы (2)
|
|
|
