 |
Номенклатура показателей надежности
|
|
|
|
Задание
Необходимо определить номенклатуру показателей надёжности для трансформатора генераторного блока электростанции.
Класс изделий - 3, группа надёжности -I, режим - непрерывный, ограничение длительности использования - вынужденное.
Решение
По таблице выбираем показатели:
— наработка на отказ;
— средний ресурс;
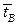— среднее время восстановления работоспособности;
— средние трудозатраты на аварийное восстановление;
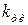— коэффициент технического использования.
Задание
Определить показатели надёжности для лампы накаливания в прожекторе на буровой установке:
Класс изделия — 2;
Группа надёжности — II;
Режим — непрерывный;
Ограничение длительности использования — вынужденное;
Для таких изделий нормируется только средний ресурс — .
| Класс изделия | Группа надёжности | Режим эксплуатации | |||||||
| непрерывный | циклический | оперативный | общий | ||||||
| назначен. огранич. | вынужд. огранич. | назначен. огранич. | вынужд. огранич. | назначен. огранич. | вынужд. огранич. | назначен, огранич. | вынужд. огранич. | ||
| 1,2,3 | для всех  или 
| ||||||||
| 1,2 |
|
|  ,
| или 
| |||||
| — |
| — | или
| ||||||
| , ,
| , , ,
| , , ,
| , , ,
| ||||||
| , ,
| , , ,
| , ,
| , ,
| ||||||
| — | ,
| — | |||||||
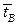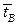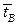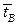
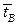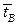| 1,2,3 |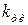
|
| 
|
|
|
| 
|
|
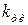
Задания для самостоятельного решения:
1. Определить вероятность повреждения в системе электроснабжения компрессорной станции, если вероятности повреждения последовательно соединенных элементов сети составляют: подстанции 35/6 кВ q = 0.03; линии 6 кВ q = 0.05; электродвигателя q = 0.005.
2. Потребитель может получать питание по двум одноцепным линиям 6 кВ. По каждой из линий он может получить 75% мощности. Вероятность выхода из строя каждой одноцепной ВЛ 6 кВ составляет 0.004. Какова вероятность сохранения электроснабжения данного потребителя?
|
|
|
3. Определить вероятность нахождения в работе 7 агрегатов из 9, если вероятность безотказной работы одного агрегата составляет 0,55.
4. При повышении напряжения в сети машина А выходит из строя с вероятностью qa =0,05, а машина В с вероятностью qb = 0,08. Найти вероятность следующих событий: а) при повышении напряжения в сети обе машины выйдут из строя; b) ни одна машина не выйдет из строя; с)машина А выйдет из строя, а машина В не выйдет.
5. Определить вероятность того, что 10 лампочек, взятых наудачу из 30, окажутся исправными, если известно, что число испорченных лампочек составляет 5% от всех имеющихся.
6. Партия из 40 изделий подвергается выборочному контролю. Условие негодности всей партии - наличие хотя бы одной бракованной детали среди 4 проверенных. Какова вероятность того, что партия не будет принята, если она содержит 10% бракованных деталей?
7. Электрическая схема, содержащая 2 блока типа А, один блок типа В и 4 блока типа С, составлена так, как это показано на cхеме. Определить вероятность разрыва цепи, неустранимого с помощью ключа К, если элементы типа А выходят из строя с вероятностью 0,3, типа В - с вероятностью 0,4, а элементы типа С - с вероятностью 0,2.
8. Имеется 6 потребителей электрического тока, для первого из которых при определённых условиях вероятность того, что произойдёт авария, приводящая к отключению потребителя, равна 0,6, для второго - 0,2, а для четырёх остальных - по 0,3.
Определить вероятность того, что генератор тока будет отключён полностью, а) если все потребители соединены последовательно, б) если потребители соединены так, как показано на схеме
9. Вероятность того, что во время сбоя работы ЭВМ возникает сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, относятся как 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,86, 0,9 и 0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
|
|
|
10. Две из четырёх независимо работающих ламп прибора отказали. Найти вероятность того, что отказали первая и вторая лампы, если вероятность отказа первой, второй, третьей и четвёртой ламп соответственно равны 0,1; 0,2; 0.3 и 0,4.
11. Коэффициент готовности объекта составляет 0,95, времена до отказа и восстановления распределены по экспоненциальным законам. Среднее время восстановления объекта 48 ч. Определить вероятность того, что объект проработает без отказа в течение: а) месяца, б) полугода, в) года (до текущего ремонта), г) четырех лет (до капитального ремонта).
12. На испытание поставлено 1000 однотипных ламп. За 3000 ч отказало 80 ламп, а за интервал от 3000 до 4000 ч отказало еще 50 ламп. Определить вероятность безотказной работы р(t), вероятность отказа q(t) для t = 3000 ч, 4000 ч и интенсивность отказов λ(t) для t = 3000 ч.
13. Общее количество изоляторов воздушных линий сетевого участка 200 000 шт. Наблюдение показало, что из взятых под наблюдение в начале года изоляторов в первом квартале вышли из строя 4000, во втором – 3000, в третьем – 2000, в четвертом – 1000. Рассчитать по этим данным и построить характеристику безотказности р(t).
14. Определить показатели надёжности для автоматического выключателя в РУ 6кВ кустовой насосной станции.
Класс изделия — 3;
Группа надёжности — I;
Режим — оперативный;
Ограничение длительности использования — вынужденное.
Статистические методы оценки, анализа и контроля надежности
Задание:
Найти наименьшее число испытаний, при котором со статистической вероятностью β = 0,99 разность относительной частоты и вероятности отказа не превышает |ε|< 0,01. Статистические значения вероятности отказа и безотказной работы соответственно равны q = 0,02; р = 0,98. Распределение случайной величины статистической вероятности β считать нормальным.
Решение:
Если известна статистическая вероятность отклонения частоты и вероятности отказа β, то по таблице интеграла вероятности или приближенно по рисунку 5 следует их найти из:
|
|
|
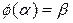т.е. при β = 0.99 α = 2.58. Далее по формуле [2]:
Задание:
Найти вероятность β того, что разность относительно частоты
события m/n и его истинной вероятности р будет меньше ε при данном числе испытаний n.
Решение:
,
а затем
по таблице интеграла вероятностей.
Задание:
Найти максимальное отношение m/n от р при заданных β и n.
Решение:
Сначала по таблице интеграла вероятностей находят α
,
Затем находят ε по формуле:
Задания для самостоятельного решения:
1. Вероятность совершения данного события 0,96. Найти наименьшее число испытаний, при котором с вероятностью 0,95 разность относительной частоты и вероятности события не превышает 0,04?
2. Определить вероятность того, что максимальное отклонение относительной частоты события m/n от вероятности 0,98 будет меньше 0,007 при числе испытаний 2000.
3. Найти максимальное отклонение Е относительной частоты события от вероятности 0,95, имеющее при числе испытаний 1500 вероятность 0,97?
Вероятностные модели для оценки надежности
Структурная надежность
Задание
Какова вероятность безотказной работы машины постоянного тока, структурная схема надежности которой состоит из коллекторно-щеточного (рк = 0,92) и подшипникового (рп = 0,95) узлов, обмоток якоря (ря = 0,99) и возбуждения (рв = 0,99). Все данные приведены для t = 5 000 ч.
Решение.
При выходе из строя любого из перечисленных узлов будет иметь место отказ всей машины. Значит, структурная схема надежности представляет собой четыре последовательно включенных блока. Согласно формуле результирующая надежность будет равна
Задание
Определить вероятность безотказной работы схемы электроснабжения
| n | |||||
| р | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 |
Решение
Для того чтобы определить вероятность безотказной работы заданной структурной схемы, преобразуем ее в 1 блок, и определим вероятность безотказной работы этого блока.
Структурная схема первого блока и ее преобразования представлены на рисунке
|
|
|
Рис. Структурная схема системы электроснабжения.
Из данной схемы видно, что 2 и 3 элементы соединены последовательно, тогда вероятность безотказной работы 2 и 3 блока можно определить по формуле:
,
где р2 и р3 – вероятность безотказной работы второго и третьего элемента структурной схемы соответственно
Тогда:
;
Исходя из того, что 1 и 23 элементы соединены параллельно, вероятность безотказной работы можно определить по формуле:
,
где q1 и q23 – вероятность того, что элемент находится в нерабочем состоянии, которая определяется по формуле:
,
Тогда:
;
Основываясь на то, что элементы 123 и 4 соединены последовательно, вычислим вероятность безотказной работы 123 и 4 блока по раннее используемой формуле:
,
;
Вероятность безотказной работы схемы и блока 1 найдем, используя формулу параллельного сложения 1234 и 5 блоков:
,
.
Задание
Дана структурная схема блока пускорегулирующей аппаратуры (рис.). Известны вероятности безотказной работы входящих в нее элементов (указаны на рисунке). Требуется найти вероятность безотказной работы всей системы.
Решение. Система состоит из двух параллельных цепей ABC и D различной надежности. Разберем цепочку ABC, которая состоит из трех блоков. На основании формулы определим надежность блока А:
где N– количество блоков в последовательном соединении
M– количество параллельных цепочек
Блок В нерезервируемый и имеет надежность РВ = 0,8. Вероятность безотказной работы блока С вычисляется по формуле:
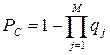
тогда вероятность безотказной работы цепочки ABC определяется
Результирующая вероятность безотказной работы всей резервированной системы будет равна
|
|
|
