 |
Модели надёжности с применением простейших потоков отказов и восстановлений
|
|
|
|
Задание
Определить показатели надёжности кабельной линии 6 кВ при следующих исходных данных (данные реальные): λ = 0,2 год-1, τ = 24часа t=l год
Решение
Время восстановления функционирования:
τ = 24ч =1/365 г
Интенсивность потока восстановления:
μ = 365год -1 = 1/τ
Коэффициент готовности:
Вероятность безотказной работы:
Наработка на отказ:
лет
Задание
1. На рисунке приведены схемы питания однотрансформаторных подстанций.
рисунок
1- Разъединитель λ = 0.02 1/год.
2- Масляный выключатель λ = 0.01 1/год.
3- Воздушная линия 6 кВ, λ = 1 1/год.
4- Предохранитель 6 кВ, λ = 0.02 1/год.
5- Отделитель, λ = 0.01 1/год.
6- Короткозамыкатель λ = 0.01 1/год.
7- Трансформатор 6/0,4 кВ λ = 0.01 1/год.
Найти среднюю частоту погашения трансформаторных подстанций по каждой из четырёх схем. Определить коэффициент готовности схемы, если
τ1, =2ч; τ 2 =6ч; τ 3 = 40ч; τ 4 =2 ч; τ 5 =2ч; τ 6 = 2ч; τ 7 =10ч.
Решение
Средняя частота погашения трансформаторных подстанций:
а) 
год-1
б) 
год-1
в) 
год-1
г) 
год-1
Наработка на отказ:
а) 
год.
б) 
год.
Общее τ для разных схем:
а) 
ч
б) 
ч
в) 
ч
г) 
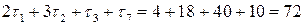ч
Коэффициент готовности:
а) 
б)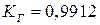 
в) 
г)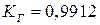
Следует отметить, что наибольшее влияние на показатели надёжности оказывает ВЛ 6 кВ, у неё наибольшая частота отзывов и наибольшее время восстановления τ.
Задание
Дано РУ 6 кВ, от которого питается 21 отходящая линия. Частота отзывов для выключателей λ = 0.003год-1, частота отзывов для линии λ = 0.03 год-1.
картинка
Найти частоту кратковременного погашения РУ 6 кВ из-за отказов линии и выключателей. Найти коэффициент готовности, если μру=182.5 1год.
Решение
Частота кратковременного погашения РУ 6 кВ складывается из λ и Xmin.
|
|
|
год
Коэффициент готовности:
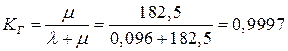
Случайные величины
Графическое представление интеграла вероятности
Рис.
Значения функции интеграла вероятностей Ф(х) для нормального закона распределения
Задание
Среднее значение времени наработки на отказ изделия составляет 12 тыс. часов. Считаем, что отклонение от среднего значения для наработки на отказ подчиняется нормальному закону распределения с дисперсией 250 тыс.ч2. Найти вероятность того, что для некоторого испытуемого изделия наработка на отказ будет находиться в пределах 12.500... 13.000 ч.
Решение
Вероятность того, что величина t будет находиться в пределах t1 < t < t2
находится по выражению:
где t2 - верхний предел заданного диапазона;
t1 - нижний предел заданного диапазона;
а - математическое ожидание случайной величины;
- среднеквадратическое отклонение случайной величины X;
D - дисперсия;
ϕ(х) - табулированный интеграл нормального распределения [1...5]. В данной работе интеграл вероятностей ϕ (х) представлен в несколько приближенном виде на рис.
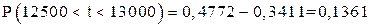
Задание
В течение 5 месяцев объём электропотребления завода (W) и число отклонений в системе автоматики (N) имели следующие значения:
| Месяцы | |||||
| W, тыс.кВт.ч. | |||||
| N, шт. |
Найти коэффициент корреляции между W и N, составить уравнение регрессии между ними. Определить (если это допустимо) возможное число отключений, если план электропотребления на некоторый месяц определён 1450 тыс.кВт.ч.
Решение
Математическое ожидание электропотребления:
, тыс.кВт.ч;
Математическое ожидание числа отклонений в системе автоматики:
, шт.
Среднеквадратическое отклонение электропотребления:
тыс.кВт.ч.;
Аналогично среднеквадратическое отклонение числа отклонений в системе автоматики 
шт.
|
|
|
Следует обратить внимание, что сумма квадратов отклонений делится по условию применения оценки среднеквадратического отклонения, то есть не на 5, а на 4, что связано с явной малостью объема выборки [2].
Коэффициент корреляции:
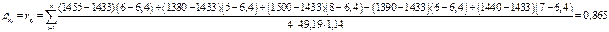
Снова используем оценку коэффициента корреляции, то есть делим на n-1=4, а не на n=5.
Уравнение регрессии:
, шт.
Коэффициент корреляции составляет 0.865, то есть достаточно высок, поэтому при заданном плане электропотребления 1450 тыс. кВт.ч, значение которого входит в интервал изменения величины W, допустимо определить возможное число отключений N:
, шт.
Случайные функции
Задание
Для района обслуживания релейной защиты и автоматики в течение пяти суток наблюдалось следующее число отказов РЗиА в характерные часы суток.
| Сутки | Часы | ||||
Доказать допустимость прогнозирования числа отказов в 19ч некоторых суток, если произошло 12 отказов в 10ч утра тех же суток. Найти математическое ожидание этого числа отказов в 19ч (если возможно).
Решение
Прежде всего, надо примерно построить график случайной функции, естественные значения в каждые сутки - это реализация, а проявления в часы суток - это сечение.
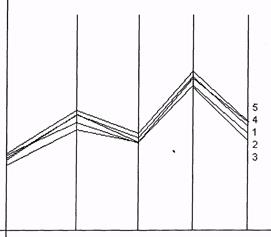
4 10 16 19 24
Процесс не имеет ярко выраженной тенденции. Он может оказаться стационарным, т.е. прогнозирование допустимо. Проверим это.
Считаем mt и σt, по сечениям (учитывая, что для σt считаются оценки).
Математическое ожидание числа отказов РЗиА:
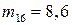
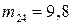
Среднеквадратическое отклонение числа отказов РЗиА:
Коэффициенты корреляции:
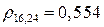
Заносим данные в расчётную таблицу:
| 4 | |||||
| 0,68 | 0,468 | 0,428 | 0,501 | ||
| 0,928 | 0,89 | 0,735 | |||
| 0,868 | 0,554 | ||||
| 0,892 | |||||
| тх | 5,2 | 11,4 | 8,6 | 17,8 | 9,8 |
| σх | 0,837 | 1,14 | 0,893 | 0,837 | 1,31 |
В таблице выделены те коэффициенты, которые позволяют построить линейное уравнение регрессии.
Для начала всё же построим корреляционную функцию (нормированную).
Она, конечно, не марковская, но монотонно убывает до определённого значения. Значит, прогнозирование можно как для стационарного процесса (но не эргодического, естественно).
|
|
|
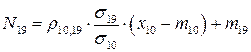
это уравнение вида Ах+В, при х=12 (по условию задачи)
отказов.
Задания для самостоятельного решения:
1. Потребитель питается от двух независимых источников, один из которых включен постоянно, а другой включается действием устройства автоматического ввода резерва (АВР). Вероятность безотказной работы источника в течение времени между плановыми остановками блока равна 0.90. Вероятность застать резервный источник в работоспособном состоянии в любой момент времени между плановыми остановками равна 0.99. Вероятность отказа в отключении равна 0.05 и во включении 0.01. Определить вероятность безотказной работы системы электроснабжения в течение времени между плановыми остановками с учетом возможности использования резервного источника, считая, что вероятностью его отказа за время восстановления рабочего источника можно пренебречь.
2. Определить вероятность безотказной работы схемы электроснабжения
| Номер элемента | 1,8 | 2,4 | 5,6 | 9,10 | ||
| р | 0,9 | 0,85 | 0,7 | 0,8 | 0,75 | 0,95 |
3. Определить вероятность безотказной работы и вероятность отказа электромагнитного контактора напряжением 0,4 кВ для момента времени t = 6 лет, зная, что интенсивность отказов по справочным данным составляет λ = 0,0005 1/год.
4. Определить вероятность безотказной работы кабельной линии напряжением 10 кВ для момента времени t = 5 лет для двух вариантов: а) среднее время восстановления составляет τ = 24 ч; б) линия не подлежит восстановлению. Параметр потока отказов по справочным данным составляет ω = 0,20 1/год,
5. При испытании пяти однотипных электрических ламп зарегистрировано время наработки до отказа: t1 = 250 сут., t2 = 295 сут., t3 = 340 сут., t4 = 210 сут., t5 =190 сут. Определить среднее время безотказной работы, интенсивность отказов и вероятность безотказной работы элементов в течение 2 лет.
6. Производятся последовательные независимые испытания пяти приборов на надёжность. Следующий прибор испытывается в том случае, если предыдущий оказался надёжным. Построить ряд распределения случайного числа испытанных приборов, если вероятность выдержать испытание для каждого из них равна 0,9. Найти математическое ожидание и дисперсию.
|
|
|
7. Аппаратура содержит 2000 одинаково надёжных элементов, вероятность отказа для каждого из которых равна 0,0005. Какова вероятность отказа аппаратуры, если он наступает при отказе хотя бы одного элемента?
8. В течение пяти суток объем электропотребления нефтепромысла (W) и число отключений в технологической системе (N) имели следующие значения:
Сутки
1 2 3 4 5
W, тыс.кВт.ч 1455 1380 1500 1390 1440
N, шт. 54 49 58 48 53
Найти коэффициент корреляции между W и N, составить уравнение регрессии между ними. Определить (если это допустимо) возможное число отключений, если план электропотребления на сутки определен 1540, тыс.кВт.ч.
9. В течение ряда лет среднее число механизированных скважин на предприятии по добыче нефти, остановленных по причине аварии в системе электроснабжения в характерные месяцы (январь, апрель, июль, октябрь и декабрь) составляли:
-----------------------------------------------------------------------------
Годы 1 Число остановленных скважин по причине аварий
1 в системе электроснабжения n, шт.
1-------------------------------------------------------------------
1Январь Апрель Июль Октябрь Декабрь
-----------------------------------------------------------------------------
1992 13 11 11 12 13
1993 12 12 12 14 11
1994 13 11 12 11 13
1995 11 12 12 12 12
1996 12 13 12 13 12
1997 13 12 11 12 12
Найти вероятное значение числа остановленных скважин в июле 1998 года, если в январе 1998 года оно составляло 15. Допустимо ли определить по январскому значению n на октябрь и декабрь.
Экономико-математические модели оптимизации надежности
Задание:
При частичном ограничении со стороны системы потребляемая предприятием максимальная мощность Рмакс = 1000 кВт снижается до величины Рогр = 850 кВт.
Определить ущерб от нарушения электроснабжения предприятия по следующим данным: Т=10 лет при параметре потока отказов λ = 1/1 год, времени восстановления питания tвосст = 10 ч.
Решение:
Среднее значение дефицита мощности:
кВт
Коэффициет вероятности дефицита мощности:
Количество недополученной электроэнергии:
кВтч
Ущерб от недополученной электроэнергии при у=0,3 тыс.руб./(кВтч):
тыс. руб.
Задание:
Электроснабжение потребителя осуществляется по одной цепи. В результате его аварийных отключений среднегодовой ущерб ΔУ1 = 10 млн.руб. Сооружение второй цепи оценивается в ΔК2 = 65млн.руб., ее эксплуатация ΔЭ2 = 2,5 млн.руб./год (при среднем сроке службы 20 лет), а средний ущерб при этом снижается до ΔУ2 = 1 млн.руб.
|
|
|
Оценить экономическую целесообразность описанного варианта повышения надежности с учетом риска, если среднеквадратическое отклонение ущерба для первого варианта (без резервирования) σ1(У) = 3 млн.руб., а для второго (с резервированием) σ2 (У) = 0,5 млн.руб.
Законы распределения ущерба считать близкими к нормальному, а уровень достоверности результата не ниже 0,999.
рн – нормативный коэффициент эффективности капитальных вложений К (в энергетике рн = 0,12).
Решение:
Первоначально сравним экономичность указанных вариантов без учета степени риска – по формуле:
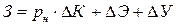
- для первого варианта:
млн.руб.
- для второго варианта:
млн.руб.
Если не учитывать цену риска, второй вариант на 10% дороже первого, т.е. экономически нецелесообразен.
Пользуясь формулой
,
определим приведенные годовые затраты с учетом риска.
Если считать случайную величину ущерба распределенной по нормальному закону, то при σ (У) ≤ 0,3У с достоверностью 0,999 можно принять Цр = 3
Тогда для первого варианта:
млн.руб.
- для второго варианта:
млн.руб.
Как видно из результатов расчета, с учетом риска второй вариант становится более привлекательным.
Задание
В энергосистеме имеется 10 генераторов по 100 МВт каждый. График нагрузок энергосистемы представляется упорядоченной диаграммой в следующем виде:
картинка
Р - нагрузка, МВт t* - время, отн.ед.
В соответствии с графиком нагрузок имеющиеся генераторы в нормальном режиме покрывают всю нагрузку энергосистемы.
Вероятность безотказной работы каждого генератора р=0,98, вероятность отказа q=0,02.
Определить есть ли необходимость в покупке дополнительных генераторов и если есть, то сколько необходимо дополнительных генераторов, если затраты на каждый резервный генератор составляет 1 у.е. в год, а удельный ущерб от недоотпуска составил 0,6 у.е.
Решение
Сразу следует сказать, что если бы генераторы имели вероятность безотказной работы р=1, то никаких новых генераторов бы не потребовалось. Однако, при не единичной вероятности безотказной работы могут возникнуть ситуации, когда вся электрическая нагрузка потребителей может быть не обеспечена.
1 этап. Без покупки дополнительных генераторов.
Дефицит мощности возникает, когда при данной ступени нагрузки выйдет из строя определенное число генераторов.
Найдем вероятность выхода из строя одного генератора из десяти:
Двух:
Трех:
Дефицит мощности в 100 МВт возникает, когда при I ступени (нагрузка в 1000 МВт) откажет один генератор, при II ступени (900 МВт) откажет два генератора, при III ступени - 800 МВт - откажет три генератора.
Вероятность дефицита в 100 МВт
Возможен дефицит и в 200 МВт. Это когда при I ступени откажут два генератора и при II ступени - три.
Крайне редко, но может возникнуть дефицит и в 300 МВт, когда при I ступени нагрузки откажут 3 генератора.
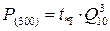
Математическое ожидание дефицита мощности:
МВт
Математическое ожидание дефицита электроэнергии умножим на число часов в году
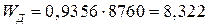млн.кВт.ч.
Математическое ожидание ущерба от недоотпуска электроэнергии
у.е./год
Купили один дополнительный генератор.
Тогда если откажет 1 генератор, дефицита мощности не будет.
Вероятность отказа двух из 11:
Трех:
Четырех:
Дефецит в 100 МВт возникает, если во время действия I ступени откажут два генератора, и при II ступени нагрузки откажут 3 генератора.
Вероятность дефецита в 200 МВт:
Математическое ожидание дефицита мощности:
МВт
Математическое ожидание дефицита эл.энергии:
млн. квт.ч
Математическое ожидание ущерба от недоотпуска электроэнергии
у.е./год
С умма затрат и ущербов по этому варианту (это возможно раз все приведено к одному к одному промежутку времени - году!)
у.е.
| Y | |||
| I | 4,993 | 4,993 | |
| II | 0,469 | 1,469 | |
| III | >0 | >2 |
Вариант с покупкой двух агрегатов смысла не имеет, т.к. затраты на два агрегата даже без всякого ущерба выше (2 млн.) чем по варианту с покупкой одного агрегата.
Т.е. оптимально необходимо купить 1 дополнительный агрегат.
Задания для самостоятельного решения:
1. При частичном ограничении со стороны системы потребляемая предприятием максимальная мощность Рмакс = 2000 кВт снижается до величины Рогр = 1850 кВт.
Определить ущерб от нарушения электроснабжения предприятия по следующим данным: Т=8 лет при параметре потока отказов λ = 1/1 год, времени восстановления питания tвосст = 12 ч.
2. Электроснабжение потребителя осуществляется по одной цепи. В результате аварийных отключений его среднегодовой ущерб составляет 10 млн руб. Сооружение второй цепи стоит 50 млн руб., ее эксплуатация – 2,5 млн руб. в год. Средний ущерб при этом снижается до 1 млн руб. в год.
Оценить экономическую целесообразность для электроснабжающей организации описанного варианта повышения надежности, если норма дисконта Е = 0,15.
3. Автономная электростанция для питания вычислительного центра состоит из восьми аккумуляторов мощностью 400 Вт каждый. Вероятность рабочего состояния аккумулятора P=0,9, аварийного соответственно Q=1-P. Нагрузка потребителя в период максимума составляет 3,2 кВт, то есть полностью покрывается мощностью. График нагрузки потребителя моделируется в виде ступеней 3,2 - 2,8 - 2,4 - 2,0 МВт длиной соответственно 0,06 – 0,12 – 0,12 -0,12 относительных единиц в долях от общего периода действия нагрузки. Требуется определить число дополнительных аккумуляторов на электростанции, если ущерб от недоотпуска электроэнергии составляет 0,812, руб/кВт. ч, а расчетные затраты на установку дополнительного аккумулятора составляют 3500, руб.
|
|
|
