Функция распределения двумерной случайной величины и ее свойства

СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН

Мы рассматривали случайные величины, возможные значения которых определялись одним числом, так называемые одномерные случайные величины. Однако в практических задачах очень часто приходится сталкиваться с экспериментами, в которых измеряют две, три,..., п характеристик, образующих комплекс или систему. Подобные эксперименты называются многомерными. Для характеристики таких экспериментов вводится понятие системы случайных величин или многомерной случайной величины.

ОПРЕДЕЛЕНИЕ МНОГОМЕРНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Систему нескольких случайных величин определенных на вероятностном пространстве , будем обозначать . Случайные величины называются составляющими или компонентами многомерной случайной величины.

Пример 3.1. Пусть вероятностный эксперимент состоит в изготовлении установочных колец токарным автоматом. Тогда каждому элементарному событию — изготовление i-го кольца - можно поставить в соответствие следующие числа:

толщина кольца;

диаметр отверстия;

предел прочности;

масса кольца.

Следовательно, эксперимент описывается 4-мерной случайной величиной: .

Для геометрической интерпретации системы случайных величин используют понятие случайной точки, или случайного вектора. Например, систему двух случайных величин рассматривают при этом как случайную точку на плоскости с координатами Х и Y, т. е. А (X;Y) или случайный вектор, направленный из начала координат в точку (X, Y) на плоскости ХОY; система трех случайных величин - случайная точка А(Х, Y, Z) или случайный вектор в трехмерном пространстве и т. д.

Пусть на вероятностном пространстве задано п случайных величин: . Совокупность этих величин называется многомерной (п-мерной) случайной величиной. Обозначим множество возможных значений п -мерной случайной величины . Любое подмножество назовем событием. Тогда множество подмножеств, которые получают из множеств путем применения конечного или счетного числа операций объединения, пересечения и дополнения, образуют -алгебру . В зависимости от того, являются ли случайные величины дискетными или непрерывными, вводится вероятность событий из .

Если случайная величина двумерная (X, Y), то множество ее возможных значений обозначается 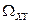; -алгебру образует система подмножеств (событий), каждое из которых может быть получено из множества вида путем применения конечного или счетного числа операций объединения, пересечения и дополнения. Вероятность любого события А вводится таким образом, чтобы она была равна вероятности наступления события, являющегося его прообразом:

.

В итоге получим распределение вероятностей двумерной случайной величины (X, Y), так как каждому событию ставится в соответствие неотрицательное число , удовлетворяющее аксиомам Колмогорова.

Тогда , где 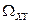- множество возможных значений двумерной случайной величины; -алгебра числового множества. - распределение вероятностей двумерной случайной величины, на­зывается вероятностным пространством двумерной случайной величины (Х,Y).

Если (X, Y) - дискретная двумерная случайная величина (т. е. когда множество 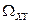конечно или счетно), то -алгебру образуют из множеств (со­бытий) вида 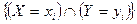. Для непрерывной двумерной случайной величины (X, Y) систему подмножеств строят из множеств (событий) вида .

 

Вопросы для самопроверки

1. С какой целью вводится многомерная случайная величина?

2. Сформулируйте определение многомерной случайной величины.

3. Что является множеством значений многомерной случайной величины?

4. Какие множества образут алгебру ?

5. Как задается распределение вероятностей многомерной случайной величины?

 

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ И ЕЕ СВОЙСТВА

 

Рассмотрим двумерную случайную величину (X, Y), множество возмож­ных значений которой .

Определение 3.1. Функцией распределения системы двух случайных вели­чин , рассматриваемой как функция переменных 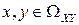называется вероятность появления события :

F(x,y) = P{(X<x) (Y<y)}. (3.1)

С геометрической точки зрения функция распределения есть вероятность попадания случайной точки (X, Y) в бесконечный квадрант с вершиной в точ­ке (х, у), лежащей левее и ниже ее (рис. 3.1).

 

 

Рис. 3.1.

Рассмотрим свойства функции распределения.

1 °. Значения функции распределения удовлетворяют неравенству

0 F(x,y) 1, .

Д о к а з а т е л ь с т в о. Свойство следует из определения функции распределения как вероятности появления события { (X < х) ( < у)}, так как вероятность всегда неотрицательное число, не превышающее единицу.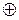

2 °. Функция распределения двумерной случайной величины F(x, у) -неубывающая функция по каждому аргументу, т. е.

;

 

.

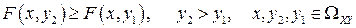Д о к а з а т е л ь с т в о. Докажем, что F(x, у) — неубывающая функция по аргументу х. Событие, состоящее в том, что составляющая X примет значение, меньшее , и при этом составляющая < у, можно разделить на сле­дующие два события:

1) X принимает значение, меньшее , при этом < у, с вероятностью

;

2) X принимает значение, удовлетворяющее неравенству х₁ Х < х₂, при этом , с вероятностью .

Согласно аксиоме 3 Колмогорова,

= + .

Отсюда

или

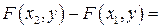
Так как вероятность — число положительное, то

.

3 °. Для функции распределения имеют место предельные соотношения:

 

Рис.3.2 Рис.3.3

 

Д о к а з а т е л ь с т в о. Так как — вероятность события , то такое событие невозможно, поскольку невозможно со­бытие следовательно, вероятность этого события равна нулю и т.д. F() есть вероятность события X < ) (Y < )}. Такое событие до­стоверно, вероятность его равна единице.

4 . При одном из аргументов, стремящихся к бесконечности (), функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:

,

где и — соответственно функции распределения случайных величин X и Y (рис. 3.2).

 

Рис.3.2 Рис.3.3

 

Д о к а з а т е л ь с т в о. Так как событие достоверно, то F(x, ) определяет вероятность события {X < х}, т. е. представляет собой функцию составляющей X. Аналогично событие {X < } достоверно и F( , у) определя­ет вероятность события 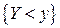, т. е. является функцией F₂(y).

Геометрически функция F₁ (x) (F₂(y)) случайной величины X () есть вероятность попадания случайной точки в полуплоскость, ограниченную спра­ва абсциссой х (сверху ординатой у).

5 °. Функция распределения F(x, у) системы двух случайных величин непрерывна слева по каждому аргументу.

Свойства 1°— 5° — характеристические. Это значит, что каждая функция F(x,y), удовлетворяющая указанным свойствам, является функцией распре­деления двумерной случайной величины (X, Y).

Функция распределения F (х, у) однозначно определяет распределение ве­роятностей P_XY(A), так как всякое событие можно представить в виде конечного либо счетного числа операций объединения, пересечения и дополнения событий .

Свойства 1°—5° функции распределения F(х, у) позволяют вычислять ве­роятности попадания двумерной случайной величины (X, Y) в любые прямо­угольные области, т. е. справедливы теоремы, приведенные ниже.

Теорема 3.1. Вероятность попадания случайной точки в бесконечную полу­полосу равна приращению функции распределения по одному из аргументов (рис. 3.3, 3.4):

 

= (3.2)

 

= (3.3)

Рис.3.4 Рис.3.5

 

Д о к а з а т е л ь с т в о. Пользуясь геометрической интерпретацией функ­ции распределения двумерной случайной величины (X, Y), легко видеть, что событие можно представить в виде объединения несов­местных событий , где

Тогда, согласно аксиоме Колмогорова 3,

= +

или по определению 3.1

,

откуда и следует выражение (3.2).

Аналогично выводится и равенство (3.3).

Теорема 3.2. Вероятность попадания случайной точки (X, ) в прямоугольник вычисляется по формуле

(3.4)

Эта вероятность находится следующим образом: из вероятности попада­ния случайной точки в полуполосу АВ вычитается вероятность попадания слу­чайной точки в полуполосу CD (рис. 3.5).

Пример 3.2. Двумерная случайная величина задана функцией распределения

Найти вероятность попадания случайной величины в квадрат, вершины которого имеют следующие координаты: (0,0); (0,1); (1, 0) и (1,1).

 

Р е ш е н и е. Искомая вероятность вычисляется по формуле (3.4):

Вопросы для самопроверки

1. Почему значения функции распределения находятся в пределах от 0 до 1?

2. Перечислите свойства функции распределения .

3. Как вычислить вероятность попадания случайной величины в прямоугольные области?

 

 

123	Поделиться:

Воспользуйтесь поиском по сайту: