 |
Распределение вероятностей двумерных дискретных случайных величин
|
|
|
|
Рассмотрим дискретную двумерную случайную величину (X, Y), т.е. величину, составляющие которой дискретны и определены на одном и том же пространстве элементарных событий 
.
Множество возможных значений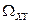 
такой случайной величины содержит конечное или счетное число точек 
:
Множество подмножеств 
образуемиз множеств вида 
.
Тогда вероятностью любого события 
назовем числовую функцию вида 
, удовлетворяющую аксиомам Колмогорова, 
и 
. Числовую функцию 
называют функцией вероятности.
Если функция вероятности задана, то на основании аксиомы 3 Колмогорова вероятность любого события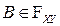 
вычисляется по формуле
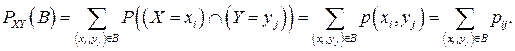. (3.5)
Определение 3.2. Законом распределения или распределением дискретной двумерной случайной величины (X, Y) называют перечень возможных значений этой величины (т.е. пар чисел 
и их вероятностей 
, характеризующих вероятность того, что составляющая Х примет значение 
и одновременно с этим составляющая Y примет значение 
.
Закон распределения или распределение дискретной двумерной случайной величины (X, Y) задают в виде табл. 3.1. Первая строка содержит все возможные значения составляющей X; первый столбец - все возможные значения составляющей Y.
Таблица 3.1
| 
| 
| … |
| … |
| 
| 
| … | 
| … |
| 
| 
| … | 
| … |
| … | … | … | … | … | … |
| 
| 
| … | 
| … |
| … | … | … | … | … | … |
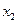
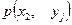
Так как события 
образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы, равна единице: 
.
Зная закон распределения двумерной случайной величины, можно найти законы распределения каждой составляющей. Например, события 
, 
,…, 
несовместны, поэтому вероятность 
того, что Х примет значение согласно аксиоме 3 Колмогорова,
|
|
|
Следовательно, распределение вероятностей составляющей Х двумерной случайной величины (X, Y), называемое маргинальным распределением, может быть задано в виде таблицы:
|
|
| … |
| … |
| 
| 
| … | 
| … |
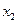
Чтобы найти вероятность 
, необходимо сложить вероятности строки 
(см. табл. 2.1):
Тогда маргинальное распределение составляющей Y двумерной случайной величины (X, Y) имеет вид:
|
|
| … | 
| … |
| 
| 
| … | 
| … |
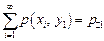
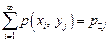
Аналогично можно определить распределение вероятностей 
- мерной случайной величины:
.
Из формулы (3.1) следует, что если двумерная случайная величина 
дискретная, то функция распределения 
имеет вид
где суммирование выполняется по всем точкам 
, для которых одновременно выполняются неравенства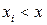 
и 
Пример 3.3. Передаются два сообщения, каждое из которых может быть независимо от другого принято с искажением или без искажения. Вероятность того, что первое (второе) сообщение принято с искажением, равна 0,1 (0,15). Рассмотрим двумерную случайную величину (X, Y), составляющие которой имеют следующие множества значений:
и 
,
где 
Найти распределение двумерной случайной величины (X, Y) и функцию распределения F(х,у).
Р е ш е н и е. Составляющие двумерной случайной величины (X, Y) дискретны. Поэтому распределение дискретной двумерной случайной величины (X, Y) определяется вероятностями:
Соответствующая таблица имеет вид:
|
| ||
| 0,765 | 0,085 | |
| 0,135 | 0,015 |
.
Согласно формуле (3.6), функцию распределения дискретной двумерной случайной (X, Y) можно записать:
Вопросы для самопроверки
1. Как вычисляется вероятность любого события 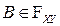при рассмотрении двумерной дискретной случайной величины?
2. Сформулируйте определение закона распределения двумерной дискретной случайной величины.
3. Как задаются маргинальные распределения составляющих двумерной дискретной случайной величины.
4. Как определяется функция распределения двумерной дискретной случайной величины.
|
|
|
|
|
|
