 |
Плотность распределения непрерывной двумерной случайной величины и ее свойства
|
|
|
|
Функцию распределения можно определить для систем любых случайных величин, как дискретных, так и непрерывных. Распределение системы непрерывных величин (т. е. величин, составляющие которых непрерывны), имеющих важное значение, обычно характеризуется плотностью распределения вероятностей.
Пусть имеется система двух непрерывных случайных величин (X, Y), которая интерпретируется случайной точкой на плоскости ХО Y. Рассмотрим на этой плоскости прямоугольник 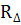 со сторонами
со сторонами  х и
х и  у, примыкающий к точке с координатами (х, у) (рис. 3.6).
у, примыкающий к точке с координатами (х, у) (рис. 3.6).

Рис. 3.6
Вероятность попадания случайной точки (X, У) в прямоугольник  вычисляется по формуле (3.4):
вычисляется по формуле (3.4):
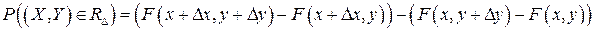 .
.
Разделим вероятность попадания случайной точки (X,Y) в прямоугольник 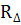 на площадь этого прямоугольника и перейдем к пределу при
на площадь этого прямоугольника и перейдем к пределу при  и
и  :
:

=  (3.7)
(3.7)
Предполагая, что  непрерывная и дифференцируемая функция, и применив теорему Лагранжа к числителю правой части равенства (3.7), получим
непрерывная и дифференцируемая функция, и применив теорему Лагранжа к числителю правой части равенства (3.7), получим
Р((х  Х< х +
Х< х +  )
) 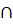 (у
(у  Y < у +
Y < у +  у)) =
у)) =  ,
,
где точка  расположена между точками
расположена между точками 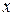 и
и  , а точка η — между
, а точка η — между 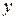 и
и  . Тогда
. Тогда
 , (3.8)
, (3.8)
так как при  и
и 
 а
а  .
.
Определение 3.3. Функция р(х, у), равная пределу отношения вероятности попадания двумерной случайной величины (X, Y) в прямоугольник со сторонами  х и
х и  у к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к нулю, называется плотностью распределения вероятностей.
у к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к нулю, называется плотностью распределения вероятностей.
Из выражения (3.8) следует, что  во всех точках, где существует смешанная производная.
во всех точках, где существует смешанная производная.
Геометрически функция z = р(х, у) - поверхность, которую называют поверхностью распределения. Если пересечь поверхность распределения плоскостью, параллельной плоскости хОу, и спроектировать полученное сечение на плоскость XOY, будем иметь кривую, в каждой точке которой плотность распределения постоянна. Такие кривые называют кривыми равной плотности.
|
|
|
Как и в одномерном случае, введем понятие элемента вероятности. Для этого воспользуемся формулой

где  при
при  х
х  0,
0,  у
у  0, которая следует из формулы (3.8) в силу определения предела.
0, которая следует из формулы (3.8) в силу определения предела.
Определение 3.4. Элементом вероятности системы двух случайных величин (X, Y) называется выражение р(х, у)  х
х  у, которое определяет вероятность попадания случайной точки (X, Y) в элементарный прямоугольник со сторонами
у, которое определяет вероятность попадания случайной точки (X, Y) в элементарный прямоугольник со сторонами  х,
х,  у, примыкающий к точке (х,у).
у, примыкающий к точке (х,у).
Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью  и опирающегося на элементарный прямоугольник
и опирающегося на элементарный прямоугольник  .
.
Вычислим теперь вероятность попадания непрерывной двумерной случайной величины (X, У) в произвольную область  Для этого разобьем область D на
Для этого разобьем область D на  элементарных прямоугольников
элементарных прямоугольников  и выберем в каждом из них точки
и выберем в каждом из них точки  . Как было сказано выше, вероятность попадания случайной точки (X, Y) в
. Как было сказано выше, вероятность попадания случайной точки (X, Y) в 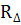 приближенно равна элементу вероятности
приближенно равна элементу вероятности  Тогда вероятность попадания непрерывной двумерной случайной величины
Тогда вероятность попадания непрерывной двумерной случайной величины  в область D приближенно равна сумме вероятностей попадания этой случайной величины в элементарные прямоугольники
в область D приближенно равна сумме вероятностей попадания этой случайной величины в элементарные прямоугольники  , т. е.
, т. е.  . Переходя к пределу при max
. Переходя к пределу при max 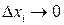 , max
, max  , получаем
, получаем
 . (3.9)
. (3.9)
С геометрической точки зрения, вероятность попадания случайной точки (X, У) в область D численно равна объему цилиндрического тела, ограниченного сверху поверхностью z = р(х,у) и опирающегося на область D.
Из формулы (3.9) получаем вероятность попадания случайной точки в прямоугольнике R:  :
:
P((X,Y)  R)=
R)=  . (3.10)
. (3.10)
Так как функция распределения есть вероятность попадания в бесконечный квадрант, то, воспользовавшись выражением (3.10), получим
F(x,y) =  (3.11)
(3.11)
Из формул (3.8) и (3.11) следует, что плотность вероятностей и функция распределения однозначно выражаются одна через другую. Следовательно, плотность вероятностей  и функция распределения
и функция распределения  полностью определяют непрерывную случайную величину.
полностью определяют непрерывную случайную величину.
|
|
|
Сформулируем свойства плотности распределения непрерывной случайной величины.
1 °.Плотность распределения двумерной случайной величины (X, Y) есть
функция неотрицательная: р(х,у)  0.
0.
Д о к а з а т е л ь с т в о. Действительно, так как плотность распределения — это предел отношения двух неотрицательных величин, то отрицательной она быть не может. 
2 °. Двойной несобственный интеграл с бесконечными пределами от плотности вероятностей равен единице:
 (x,y)dxdy= 1. (3.12)
(x,y)dxdy= 1. (3.12)
Д о к а з а т е л ь с т в о. Свойство 2 ° следует из того, что интеграл (3.12) есть не что иное, как вероятность попадания случайной точки (X, Y) на всю плоскость XOY, а это достоверное событие. 
Пример 3.4. Двумерная случайная величина  распределена с постоянной плотностью внутри квадрата R, вершины которого имеют координаты: (0; 0), (0; 2), (2; 0), (2; 2).
распределена с постоянной плотностью внутри квадрата R, вершины которого имеют координаты: (0; 0), (0; 2), (2; 0), (2; 2).
Найти плотность вероятностей  и функцию распределения
и функцию распределения  .
.
Р е ш е н и е. Плотность вероятностей двумерной случайной величины  , согласно условию задачи, можно записать:
, согласно условию задачи, можно записать:
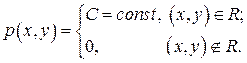

Постоянную С определим, воспользовавшись свойством 2  плотности вероятностей:
плотности вероятностей:
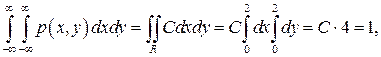
откуда С =  . Таким образом,
. Таким образом, 
Функцию распределения найдем по формуле (3.11):
а) пусть х  0 или
0 или 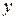
 0, тогда
0, тогда
F(x,y)=P((X<x) 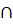 (Y< y))=
(Y< y))=  ,
,
так как 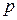 (ξ, η) = 0 при (ξ, η)
(ξ, η) = 0 при (ξ, η)  R;
R;
б) пусть 0< 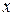
 2 и 0
2 и 0  2, тогда
2, тогда

 =
=
= 
в) пусть 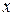 >2 и 0<
>2 и 0< 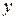
 2, тогда
2, тогда

 =
= 

г) пусть 0 < 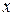
 2 и
2 и 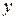
 , тогда
, тогда

 =
= 
д) пусть х > 2и у > 2, тогда

 =
= 
Таким образом, функция распределения двумерной случайной величины  имеет вид
имеет вид


Пример 3.5. Функция распределения двумерной случайной величины задана выражением
F(x,y) = 
Вычислить вероятность P((0  X
X  1)
1) 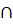 (0
(0 

 1)).
1)).
Р е ш е н и е. Искомую вероятность определим по формуле (3.9):
Р((0  Х
Х  1)
1) 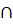 (0
(0 

 1)) =
1)) =  dy
dy  (x,y)dx,
(x,y)dx,
где плотность вероятностей 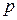 (х, у) определим по формуле (3.8):
(х, у) определим по формуле (3.8):


Тогда 

 =
= 
Вопросы для самопроверки
- Сформулируйте определение плотности распределения вероятностей
 .
. - Как вычислить плотность, если задана функция распределения?
3. Сформулируйте определение элемента вероятностей системы двух случайных величин.
- Перечислите свойства плотности распределения вероятностей.
|
|
|
3.5. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ, ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
ВЕРОЯТНОСТЕЙ СОСТАВЛЯЮЩИХ ДВУМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.
УСЛОВНЫЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И УСЛОВНЫЕ ПЛОТНОСТИ
РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
Зная закон распределения системы двух случайных величин, можно определить законы распределения отдельных величин, входящих в систему. В § 3.1 мы показали, что если один из аргументов стремится к  , а другой остается переменным, то функция распределения F(x, у) системы случайных величин (X, Y) становится функцией распределения одной из составляющих:
, а другой остается переменным, то функция распределения F(x, у) системы случайных величин (X, Y) становится функцией распределения одной из составляющих:  =
=  .
.
Если двумерная случайная величина (X, Y) - непрерывная и ее функция распределения задана плотностью вероятностей р (х, у), т. е.
F(x,y)= 
то функции распределения составляющих X и Y определяются по формулам:
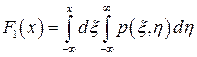 (3.13)
(3.13)
 =
=  . (3.14)
. (3.14)
Дифференцируя выражения (3.13) и (3.14) по соответствующим переменным, согласно теореме о дифференцировании определенного интеграла по переменному верхнему пределу, получим выражение для плотностей распределения вероятностей составляющих X и Y:

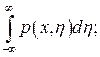 (3.15)
(3.15)
 . (3.16)
. (3.16)
Зная функцию распределения системы, по формулам (3.13) —(3.16) можно определить функции распределения отдельных величин, входящих в систему. Но обратную задачу в общем случае решить нельзя, т. е., зная только функции распределения отдельных случайных величин, входящих в систему, не всегда можно найти функцию распределения системы. Нужно знать также зависимость между величинами, входящими в систему. Эта зависимость может быть охарактеризована с помощью условных законов распределения.
Определение 3.5. Условным законом распределения или условным распределением составляющей X ( ), входящей в систему (X, Y), называется ее распределение, вычисленное при условии, что другая случайная величина Y (X) приняла определенное значение у (х).
), входящей в систему (X, Y), называется ее распределение, вычисленное при условии, что другая случайная величина Y (X) приняла определенное значение у (х).
Определим выражение для условной функции распределения составляющей X ( ) непрерывной двумерной случайной величины (X, Y):
) непрерывной двумерной случайной величины (X, Y):
 .
.
Для этого введем в рассмотрение два события А = {X < х) и 
 .
.
Вероятность события АВ ={(Х < х) 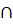 (у
(у  Y < у +
Y < у +  у)} на основании теоремы умножения двух событий А и В равна:
у)} на основании теоремы умножения двух событий А и В равна:
|
|
|
P((X<x) 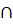 (y
(y  Y<y+
Y<y+  y)}=P(y
y)}=P(y  Y<y+
Y<y+  y)P((X <x
y)P((X <x  y<Y<y+
y<Y<y+  y)),
y)),
откуда по формуле (3.10) при условии, что Р(у  Y < у +
Y < у +  у) > 0, получим
у) > 0, получим
P((X<x 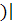 (y
(y  Y<y +
Y<y +  y))=
y))= 
 . (3.17)
. (3.17)
Разделив в равенстве (3.17) числитель и знаменатель правой части на  у и предположив, что плотность р(х, у) непрерывна в рассматриваемой области, согласно теореме о среднем,
у и предположив, что плотность р(х, у) непрерывна в рассматриваемой области, согласно теореме о среднем,
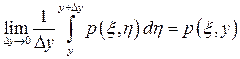 .
.
Тогда

или
 (3.18)
(3.18)
где 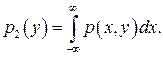
Аналогично
F(y  =
=  (3.19)
(3.19)
где

Дифференцируя условные функции распределения F(x  ) и F(y
) и F(y  ) по х и у соответственно, получаем формулы для вычисления условных плотностей распределения вероятностей составляющих X и Y непрерывной двумерной случайной величины (X, Y):
) по х и у соответственно, получаем формулы для вычисления условных плотностей распределения вероятностей составляющих X и Y непрерывной двумерной случайной величины (X, Y):

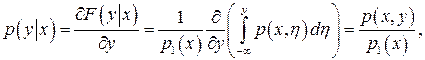
откуда следует теорема умножения плотностей вероятностей.
Теорема 3.3. Плотность распределения непрерывной двумерной случайной величины (X, Y) равна плотности распределения одной из величин, входящих в систему, умноженной на условную плотность распределения другой величины, вычисленную при условии, что первая величина приняла заданное значение:
 или
или  .
.
Рассмотрим дискретную двумерную случайную величину (X, Y), составляющие которой определены на одном пространстве элементарных событий, и обозначим их значения: 
Пусть случайная величина (X,  ) приняла некоторое значение
) приняла некоторое значение  ; при этом другая случайная величина X может принимать любое из значений
; при этом другая случайная величина X может принимать любое из значений  , …
, …
Тогда условная вероятность события А =  , если наблюдалось событие В =
, если наблюдалось событие В =  , согласно формуле Р(А | В) =
, согласно формуле Р(А | В) =  , равна
, равна
P((X=  )
)  Y =
Y =  )=
)=  .
.
Обозначая эту вероятность р (  ) получаем
) получаем
р (  )=
)=  .
.
Совокупность условных вероятностей р(х1  ), р(х2
), р(х2  ),..., р(
),..., р(  )…, отвечающих условию Y =
)…, отвечающих условию Y =  называют условным распределением составляющей X при Y =
называют условным распределением составляющей X при Y =  дискретной двумерной случайной величины (X, Y).
дискретной двумерной случайной величины (X, Y).
Аналогично условное распределение составляющей Y при  дискретной двумерной случайной величины (X, Y) — это совокупность условных вероятностей p (
дискретной двумерной случайной величины (X, Y) — это совокупность условных вероятностей p ( отвечающих условию
отвечающих условию  ,
,
где 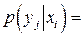
 .
.
Отметим, что сумма вероятностей условного распределения равна единице.
Действительно,

Аналогично 
Условная функция распределения F(x  ) или F(y
) или F(y  ) дискретной случайной двумерной величины, заданной табл. 3.1, имеет вид:
) дискретной случайной двумерной величины, заданной табл. 3.1, имеет вид:
F(x  ) =P((X<x)
) =P((X<x)  Y=y))=
Y=y))=  =
= 

или

 =
= 

Пример 3.6. Случайная величина (X, Y) распределена с постоянной плотностью p(х, y) = const = С внутри квадрата R (рис. 3.7),

Рис.3.7
вершины которого имеют координаты (-2; 0), (0; 2), (2; 0) и (0; -2). Определить плотность распределения случайной величины (X, Y) и условные плотности распределения вероятностей р (х | у), р (у  ) составляющих.
) составляющих.
Р е ш е н и е. Плотность распределения вероятностей двумерной случайной величины (X, У) в силу свойства 
|
|
|
 т.е. p(x,y)=
т.е. p(x,y)= 
Определим плотности 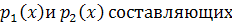 X и Y двумерной случайной величины (X,Y):
X и Y двумерной случайной величины (X,Y):

Аналогично

Компактнее плотности  и
и 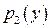 записать в виде:
записать в виде:


Пусть 
 =
= 
Если  , то
, то
 =
= 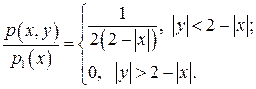
Вопросы для самопроверки
1. Укажите формулы для вычисления функций распределения и плотностей распределения вероятностей составляющих двумерной случайной величины.
2. Сформулируйте определения условных законов распределения составляющих двумерной случайной величины.
3. По каким формулам вычисляются условные функции распределения, условные законы распределения составляющих двумерной случайной величины?
|
|
|


