 |
Порядок проведения занятия
|
|
|
|
Задание 1
Определите значение параметра Rz шероховатости поверхности по приведенным результатам обработки профилограмм с учетом коэффициента вертикального увеличения профилографа. Выберите ближайшее большее стандартное значение параметра шероховатости по справочным данным, приведенным в прил. Д.
Таблица 9.1
| Расстояние от базовой линии до низших точек выступов, мм | Вариант | |||||||||
| h1 | ||||||||||
| h2 | ||||||||||
| h3 | ||||||||||
| h4 | ||||||||||
| h5 | ||||||||||
| h6 | ||||||||||
| h7 | ||||||||||
| h8 | ||||||||||
| h9 | ||||||||||
| h10 | ||||||||||
| Вертикальное увеличение | 103 | 2×103 | 20×103 | 104 | 2×104 | 103 | 2×103 | 20×103 | 104 | 2×104 |
Окончание табл. 9.1
| Расстояние от базовой линии до низших точек выступов, мм | Вариант | |||||||||
| h1 | ||||||||||
| h2 | ||||||||||
| h3 | ||||||||||
| h4 | ||||||||||
| h5 | ||||||||||
| h6 | ||||||||||
| h7 | ||||||||||
| h8 | ||||||||||
| h9 | ||||||||||
| h10 | ||||||||||
| Вертикальное увеличение | 103 | 2×103 | 20×103 | 104 | 2×104 | 103 | 2×103 | 20×103 | 104 | 2×104 |
|
|
|
Задание 2
Выбрать параметр шероховатости Ra соответствующий номинальному диаметру и полю допуска вала, приведенным в табл. 4.3. Для этого необходимо определить предельные отклонения вала и рассчитать допуск. Следует помнить, что величину параметра Rz рекомендуется назначать не более 0,33 от величины допуска на размер, а значение параметра Ra примерно в четыре раза меньше чем значение параметра Rz.
Таблица 4.3
| Варианты | ||||||||||
| Номинальный размер и поле допуска | 40h7 | 120g8 | 80f7 | 130js6 | 50e7 | 70d8 | 120m7 | 10s6 | 36k7 | 45p6 |
Окончание табл. 4.3
| Варианты | ||||||||||
| Номинальный размер и поле допуска | 20f8 | 60t7 | 125n6 | 70k8 | 35m8 | 135g6 | 80t9 | 25p8 | 75e8 | 85js7 |
Задание 3
Получить у преподавателя рабочий чертеж детали. Провести анализ простановки шероховатости на чертеже. Отметить и расшифровать правильное обозначение. Указать на имеющиеся недостатки
Оформление отчета
Отчет должен содержать:
1. Название темы и цель работы.
2. Выполненные задания 1-3 и оформленные по форме, приведенной в табл. 9.2.
Таблица 9.2
| Задание №1 | |
| Расчет значения параметра шероховатости Rz | |
| Стандартное значение параметра шероховатости Rz | |
| Задание №2 | |
| Значение предельных отклонений и величина допуска | |
| Расчет параметра Rz | |
| Значение параметра шероховатости Ra | |
| Задание №3 | |
| Анализ простановки шероховатости на чертеже |
9.3. Контрольные вопросы
1. Почему невозможно получить идеально ровную поверхность?
2. Дайте определение «базовая длина».
3. Какие параметры для оценки высоты неровностей Вы знаете?
4. Как определяется параметр Rz?
5. Когда применяют для обозначения шероховатости поверхности знак  ?
?
6. Когда базовая длина не ставится в обозначении шероховатости поверхности?
|
|
|
7. В каких единицах указываются в условном обозначении высотные параметры шероховатости поверхности?
Модуль 3. Взаимозаменяемость типовых соединений
Допуски угловых размеров, конических соединений
Цель занятия: Изучить основы взаимозаменяемости угловых размеров и конических соединений. Научиться нормировать и обозначать на чертежах допуски и посадки для углов и конусов.
Основные положения.
При конструировании машин наиболее часто используют нормальные углы, которые можно разделить на три группы:
1) нормальные углы общего назначения;
2) нормальные углы специального применения;
3) специальные углы, размеры которых связаны с расчетными зависимостями и которые нельзя округлить до нормальных углов.
Размеры углов первой группы приведены в табл. 10.1 и 10.2. Пример углов второй группы показан в табл. 10.3.
Таблица 10.1
Размеры и ряды нормальных углов общего назначения
| Р я д | ||||||||
| 00 | 00 0030¢ 10 20 30 | 00 0015¢ 0030¢ 0045 10 1030¢ 20 2030¢ 30 40 | 150 | 150 200 | 150 180 200 220 250 | 600 | 600 750 | 600 650 700 750 800 850 |
| 300 | 300 | 300 350 400 | 900 | 900 | 900 1000 1100 | |||
| 50 | 50 80 | 50 60 70 80 90 100 120 | 450 | 450 | 450 500 550 | 1200 | 1200 | 1200 1350 1500 1800 2700 3600 |
| При выборе углов 1-й ряд следует предпочитать 2-му, 2-й — 3-му. |
Таблица 10.2
Углы конусов и уклонов нормальных конусностей
                  
d D С = С – конусность; a – угол конуса; D – диаметр большого основания конуса; a / 2 – угол уклона; L d – диаметр малого основания конуса
| |||||||||
| Конус- ность | Угол конуса a | Угол уклона a/2 | Конус- ность | Угол конуса a | Угол уклона a/2 | ||||
| Градус | Радиан | Градус | Радиан | Градус | Радиан | Градус | Радиан | ||
| 1:200 | 17¢11,3² | 0,00500 | 8¢35,6² | 0,002500 | 1:7 | 8°10¢16 | 0,142615 | 4°5¢8 | 0,071307 |
| 1:100 | 34¢22,6² | 0,010000 | 17¢11,3² | 0,005000 | 1:5 | 11°25¢16 | 0,199337 | 5°42¢38 | 0,099669 |
| 1:50 | 1°8¢45 | 0,019990 | 34¢22,6² | 0,010000 | 1:3 | 18°55¢28 | 0,330297 | 9°27¢44 | 0,165149 |
| 1:30 | 1°54¢34 | 0,033330 | 57¢17,5²1 | 0,016665 | 1:1,866 | 30° | 0,523599 | 15° | 0,261799 |
| 1:20 | 2°51¢51 | 0,049990 | °25¢55 | 0,024995 | 1:1,207 | 45° | 0,785398 | 22°30¢ | 0,392699 |
| 1:15 | 3°49¢5 | 0,066642 | 1°54¢32 | 0,033321 | 1:0,866 | 60° | 1,047198 | 30° | 0,523299 |
| 1:12 | 4°46¢18 | 0,083285 | 2°23¢9 | 0,041643 | 1:0,652 | 75° | 1,308997 | 37°30¢ | 0,654498 |
| 1:10 | 5°43¢29 | 0,099915 | 2°51¢44 | 0,049957 | 1:0,500 | 90° | 1,570796 | 45° | 0,785398 |
| 1:8 | 7°9¢9 | 0,124838 | 3°34¢34 | 0,062419 | 1:0,289 | 120° | 2,094395 | 60° | 1,047198 |
|
|
|
Таблица 10.3
Углы конусов и уклонов конусностей специального назначения
| Конус- | Угол конуса a | Угол уклона a2 | Конус Морзе | |||
| ность | Градус | Радиан | Градус | Радиан | № | Диаметр, мм |
| 1:19,212 | 2058¢54² | 0,052039 | 1°29¢27² | 0,026020 | 9,045 | |
| 1:20,047 | 2051¢26² | 0,049872 | 1°25¢43² | 0,024936 | 12,065 | |
| 1:20,020 | 2051¢41² | 0,049940 | 1°25¢50² | 0,024970 | 17,780 | |
| 1:19,922 | 2052¢32² | 0,050185 | 1°26¢16² | 0,025093 | 23,825 | |
| 1:19,254 | 2058¢31² | 0,051926 | 1°29¢16² | 0,025963 | 31,267 | |
| 1:19,002 | 3000¢53² | 0,052614 | 1°30¢27² | 0,026307 | 44,399 | |
| 1:19,180 | 2059¢12² | 0,052126 | 1°29¢36² | 0,026063 | 63,348 |
Допуском угла  (от англ. Angle Tolerance) называют разность между наибольшим
(от англ. Angle Tolerance) называют разность между наибольшим  и наименьшим
и наименьшим  предельными углами (рис.10.1). Допуски угловых размеров назначают по ГОСТу 8908 в зависимости от длины
предельными углами (рис.10.1). Допуски угловых размеров назначают по ГОСТу 8908 в зависимости от длины  меньшей стороны угла.
меньшей стороны угла.
Допуск угла может выражаться:
- в угловых единицах радианной и градусной мер  (точное значение);
(точное значение);
- в округленном значении градусной меры  ;
;
- в линейных единицах  - длиной противолежащего отрезка на перпендикуляре к стороне угла на расстоянии
- длиной противолежащего отрезка на перпендикуляре к стороне угла на расстоянии  от вершины (рис.10.1).
от вершины (рис.10.1).

Рис. 10.1. Схема допуска угла
Связь между допусками в угловых и линейных единицах выражается следующей зависимостью:
 (10.1)
(10.1)
где  - мкм;
- мкм; 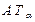 - мкрад;
- мкрад;  - мм.
- мм.
Напоминаем, что 1 мкрад (микрорадиан) = 10-6 радиан. Соотношения между градусом и радианом следующие:
1° = 2p / 360 = 0,017453 рад = 17453 мкрад, (10.2)
1¢ = 0,00029088 рад» 291 мкрад; (10.3)
1рад = 360° / 2p = 57° 17¢ 44,8². (10.4)
При малых углах (  < 10°) синус и тангенс угла практически равен величине угла, выраженного в радианах.
< 10°) синус и тангенс угла практически равен величине угла, выраженного в радианах.
|
|
|



 = 2 tg a/2, где
= 2 tg a/2, где