Разбивка главных точек круговых кривых

В плане ось дороги представляет собой сочетание прямых и кривых участков. В каждой вершине поворота трассы две смежные линии ее сопрягаются кривой. Кривые могут иметь форму круговой или суммарной кривой. Суммарная кривая состоит из двух переходных кривых и круговой кривой.

Рассмотрим круговую кривую (рисунок 3.1). Круговая кривая – это дуга окружности, вписанная в угол, образованный двумя смежными линиями трассы. Круговая кривая имеет три главные точки и шесть элементов.

Главными точками круговой кривой являются начало круговой кривой (НКК), конец круговой кривой (ККК) и середина круговой кривой (СКК).

На плане и на местности эти точки могут быть получены, если известны следующие элементы кривой:

 

Рисунок 3.1 – Элементы круговой кривой

1 – угол поворота трассы φ;

2 – радиус круговой кривой R;

3 – расстояние от вершины угла поворота ВУП до начала или конца кривой, которое называется тангенс Т;

4 – длина кривой, расстояние от ее начала до ее конца К;

5 –расстояние от вершины угла поворота до середины кривой, которое называется биссектриса кривой Б;

6 – домер, показывающий, на сколько путь от начала до конца кривой по касательной больше, чем по кривой Д.

Угол поворота трассы (φ) измеряют при трассировании, а величину радиуса кривой (R) выбирают в соответствии с техническими условиями.

Остальные элементы круговой кривой могут быть определены из прямоугольного треугольника (О – НКК – ВУП) на рисунке 3.2 по следующим формулам:

 

Т - дорожный тангенс, м:

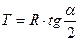, (3.1)

где R - радиус кривой,м.

a - угол поворота трассы, град.

 

K - длина круговой кривой, м:

, (3.2)

Б –биссектриса угла поворота, м:

 

(3.3)

 

Д – домер, м:

Д = 2∙Т – К. (3.4)

 

Определим значение пикетажа основных точек кривой (начало круговой кривой НКК и конец круговой кривой):

 

 

ВУП №1 = ПК 11+00,00 α =43°, R = 200 м.

ВУП №2 = ПК 31+50,00 α =24°, R = 1000 м.

 

Определим пикетажные значения начала и конца круговой кривой для:

 

ВУП №1 ПК 1 + 00,00 ВУП №2 ПК 31 +50,00

- Т 0 + 88,78- Т 0 +212,55

НКК1 ПК 10 + 11,22 ПК 29 + 37,45

+ К 117 + 40,00+ К + 418,66

ККК1 ПК 11+ 28,62 ККК1 ПК 33 + 56,11

 

 

Значения пикетажа круговой кривой совпадают в обоих случаях, значит расчет выполнен верно.

Пикетаж разбиваем до вершины угла поворота, затем в вершине угла поворота разбиваем круговую кривую, после чего продолжаем разбивку пикетажа. Аналогично производим расчет для второй круговой кривой. Результаты расчетов элементов прямых и кривых в плане, для всех вершин, представлены в таблице 3.1.

Поскольку радиус кривой довольно мал, что приводит к резкому возрастанию центробежной силы на участках поворота трассы, то следует сопрячь прямой участок и круговую кривую переходной кривой. Наличие переходной кривой обеспечивает плавность хода на повороте дороги.

Рисунок 3.2 – Разбивка хода с симметричными переходами (клотоидными кривыми)

 

Круговая кривая содержит следующие элементы проектирования.

 

Рассчитаем первую круговую кривую с радиусом 200 метров.

Найдём разбивочный угол β:

рад. (3.5)

 

где – длина переходной кривой;

l_пк= 10 м - длина переходной кривой,

R – радиус круговой кривой.

 

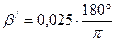= 1°43¢

Проверяем возможность разбивки переходной кривой:

 

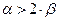(3.6)

 

где α- угол поворота.

 

43°>1°43¢*2

Так как условие выполняется, разбиваем переходную кривую.

Находим сдвижку круговой кривой (р):

 

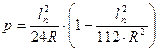, (3.7)

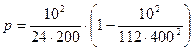=0,019 м.

 

Определяем длину сокращенной круговой кривой для угла 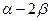(К₁), полную длину закругления (К₂), домер (Д).

 

(3.8)

 

 

Для первой переходной кривой имеем:

α =64° (право)

R =200 м,

Т₁ =Т+t = 78,88+ 9,9= 88,78 м, (3.9)

Б₁ = Б+ Р = 15,05+0,019 = 15,069,

К = 200*3,14*(43°-2*1°43¢)/180 = 97,4 м,

К₁ = 97,4 + 2*10 = 117,40 м

Д₁ = 2*7,535 – 15,07= 0 м.

Данные о кривых в плане заносим в таблицу 3.1.

 

 

Таблица 3.1 – Данные о кривых в плане

ВУ	Угол поворота	кривая	прямая
ПК ВУ	Лево	Право	Элементы кривой, м	ПКНЗ	ПККЗ	Прямая вставка Р, м	Румб, г
R	L	T	K	Б	Д
1 ВАРИАНТ	1011,22	ЮЗ 220
ВУ1	ПК11+0	-	430			88,78	117,40	15,07	38,49	ПК10+11,22	ПК11+28,62
1808,83	ЮЗ 650
ВУ2	ПК31+50	-	240		-	212,55	418,66	53,82	22,34	ПК29+37,45	ПК33+56,11
943,89	СЗ 850
2 ВАРИАНТ	1581,02	ЮЗ 700
ВУ1	ПК16+0	8˚	-			22,43	22,43	1,5	0,63	ПК15+81,02	ПК16+3,45
309,08	СЗ 600
ВУ2	ПК20+0	100	-		-	174,44	174,44	3,91	4,8	ПК19+12,53	ПК20+86,47
1813,53	ЮЗ 950

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: