 |
|дисперсионным. |равенстве средних. |нормально распределены, их дисперсии равны. |фактором. |отвергается. |принимается. |однофакторный и многофакторный
|
|
|
|
|дисперсионным
|дискриминантным
~При дисперсионном анализе проверяется нулевая гипотеза о:
|равенстве среднего некоторому значению
|равенстве дисперсий
|равенстве средних
|различии средних
|различии дисперсий
~Вид нулевой гипотезы «Н0» при дисперсионном анализе:
| 
~Вид альтернативной гипотезы «Н1» при дисперсионном анализе:
| 
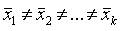
~Дисперсионный анализ может применяться, если для выборок выполнены условия:
|равномерно распределены, их дисперсии равны
|нормально распределены, их дисперсии неравны
|равномерно распределены, их дисперсии неравны
|нормально распределены, их дисперсии равны
|показательно распределены, их дисперсии равны
~Показатель, который оказывает влияние на конечный результат, называется:
|фактором
|аргументом
|откликом
|уровнем
|признаком
~Фактор - это:
| показатель, который оказывает влияние на конечный результат
|показатель, который не оказывает влияния на конечный результат
|значение измеряемого признака
|значение групповой средней
|показатель, который оказывает влияние на промежуточный результат
~Отклик на фактор - это:
| значение измеряемого признака
|показатель, который оказывает влияние на конечный результат
|показатель, который не оказывает влияния на конечный результат
|значение групповой средней
|показатель, который оказывает влияние на промежуточный результат
~Значение измеряемого признака в дисперсионном анализе называется:
|фактором
| откликом
|аргументом
|уровнем
|признаком
~При дисперсионном анализе если фактор оказывает воздействие на величину отклика, то нулевая гипотеза о равенстве средних:
|отвергается
|
|
|
|принимается
|игнорируется
|формулируется заново
|не рассматривается
~При дисперсионном анализе если фактор не оказывает воздействия на величину отклика, то нулевая гипотеза о равенстве средних:
|отвергается
|игнорируется
|формулируется заново
|не рассматривается
|принимается
~В зависимости от количества изучаемых действий на явления дисперсионный анализ делится на:
|простой и сложный
|одинарный и множественный
|однофакторный и многофакторный
|дискретный и непрерывный
|парный и двухвыборочный
~Выборочные данные для однофакторного дисперсионного анализа оформляют в виде:
|диаграммы
|рисунка
|таблицы
|формулы
|схемы
~При дисперсионном анализе общая дисперсия разбивается на:
|простую и сложную
|дискретную и непрерывную
| факторную и остаточную
|абсолютную и относительную
|постоянную и переменную
~Формула факторной дисперсии:
| 
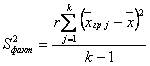
~Формула остаточной дисперсии:
| 
| 
++++++++
| 
| 
| 
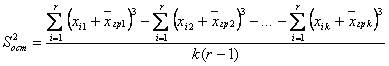
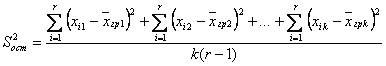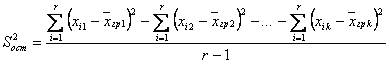
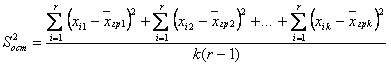
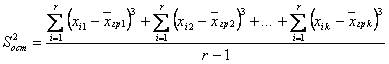
~ Формула общей дисперсии:
| 
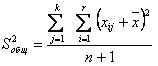
~Дисперсия, которая соответствует влиянию фактора на изменение средних значений выборки, называется:
|остаточной
|общей
|факторной
|средней
|простой
~Дисперсия, возникающая по случайными причинами и не влияющая на изменение средних значений выборки, называется:
|остаточной
|факторной
|общей
|средней
|простой
~Сумма факторной и остаточной дисперсий называется:
|частичной
|положительной
|отрицательной
|общей
|выборчной
~При дисперсионном анализе используется критерий:
|Стьюдента
|Пирсона
|Фишера
|Колмогорова-Смирнова
|Манна-Уитни
~Критерий Fрасч, используемый при дисперсионном анализе, определяется по формуле:
| 
| 
| 
+++
| 
| 
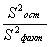
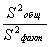
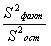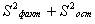
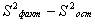
~Аналогом однофакторного дисперсионного анализа является критерий:
|
|
|
