 |
|Ч. Спирменом. |Ф. Гальтон. |парную, множественную. |прямую, обратную. |y=f(x1, x2,…, xn). |линейное. |параболическое. |гиперболическое
|
|
|
|
|Ч. Спирменом
~Коэффициент ранговой корреляции Спирмена:
| 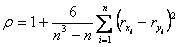
| 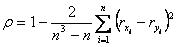
| 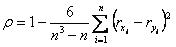
| 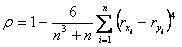
| 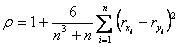
~ 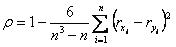 :
:
|линейный коэффициент корреляции Пирсона
|коэффициент контингенции Пирсона
|коэффициент сопряженности Чупрова
|коэффициент ранговой корреляции Спирмена+
|коэффициент ассоциации Юла
~Коэффициент ранговой корреляции Спирмена принимает значения в промежутке:
|[0; 1]
|[-1; 0]
|[-1; 1]
|[-10; 10]
|[1; 10]
~Коэффициент ранговой корреляции Спирмена используется для определения тесноты связей как между …, так и между … признаками.
|относительными, абсолютными
|простыми, сложными
|базовыми, цепными
|количественными, качественными+
|экстенсивными, интенсивными
~Коэффициент ранговой корреляции Спирмена применяется, если объемы выборок удовлетворяют условию:
|1≤ n1, 2≤ 50
|5≤ n1, 2≤ 40
|5≤ n1, 2≤ 30
|4≤ n1, 2≤ 40
|3≤ n1, 2≤ 40
~Термин «регрессия» ввел:
|Ф. Гальтон
|Р. Фишер
|К. Пирсон
|А. Кетле
|В. Уэлдон
~Метод статистической обработки данных, позволяющий измерить связь между одной или несколькими причинами и следствием - это … анализ.
|регрессионный +
|дисперсионный
|дискриминантный
|корреляционный
|статистический
~По количеству признаков различают регрессию:
|простую, сложную
|парную, множественную
|слабую, сильную
|прямую, обратную
|постоянную, переменную
~По направлению связи различают регрессию:
|парную, множественную
|простую, сложную
|прямую, обратную
|слабую, сильную
|постоянную, переменную
~Если результативный признак рассматривается как функция от одного аргумента, то регрессия:
|одинарная
| парная+
|множественная
|простая
|линейная
~Если результативный признак рассматривается как функция от нескольких аргументов, то регрессия:
|
|
|
|парная
|одинарная
| множественная
|простая
|линейная
~Общий вид уравнения парной регрессии:
|y=f(x1, x2, …, xn)
|y=f(x)+
|y=ax+b
|y=a+b/x
|y= axb
~Общий вид уравнения множественной регрессии:
|y=f(x1, x2, …, xn)
|y=ax+b
|y=a+b/x
|y= axb
|y=f(x)
~Линейное уравнение парной регрессии:
|y=eax+b
|y=a+b/x
|y=a+b1x+b2x2
|у=a+bx+
|y=abx
~Экспоненциальное уравнение парной регрессии:
|у=a+bx
|y=a+b/x
|y=eax+b+
|y=a+b1x+b2x2
|y=abx
~Гиперболическое уравнение парной регрессии:
|y=a+b/x+
|y=eax+b
|у=a+bx
|y=a+b1x+b2x2
|y=abx
~Параболическое уравнение парной регрессии:
|y=a+b/x
|y=eax+b
|у=a+bx
|y=a+b1x+b2x2
|y=abx
~Показательное уравнение парной регрессии:
|y=a+b1x+b2x2
|y=abx
|y=a+b/x
|y=eax+b
|у=a+bx
~у=a+bx - … уравнение парной регрессии.
|экспоненциальное
|линейное
|гиперболическое
|параболическое
|показательное
~y=a+b1x+b2x2 - … уравнение парной регрессии.
|линейное
|экспоненциальное
|гиперболическое
|показательное
|параболическое
~y=a+b/x - … уравнение парной регрессии.
|показательное
|гиперболическое
|параболическое
|линейное
|экспоненциальное
~y=eax+b - … уравнение парной регрессии.
|параболическое
|линейное
|экспоненциальное
|гиперболическое
|показательное
~y=abx - … уравнение парной регрессии.
|экспоненциальное
|гиперболическое
|параболическое
|линейное
| показательное
~Построение уравнения регрессии сводится к оценке:
|независимой переменной
|коэффициентов
|результативного признака
|факторного признака
|зависимой переменной
~Коэффициенты уравнения регрессии определяются с помощью метода:
|наименьших квадратов
|доверительных интервалов
|корреляционного анализа
|статистического наблюдения
|дисперсионного анализа
~Суть метода наименьших квадратов:
| 
~Формула определения свободного коэффициента линейного уравнения парной регрессии:
|
|
|
| 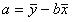
~Формулы определения коэффициентов линейного уравнения парной регрессии:
|
| 
~Для оценки статистической значимости коэффициентов регрессии используется критерий:
|Фишера
|Пирсона
|Стьюдента
|Манна-Уитни
|Колмогорова-Смирнова
~Нулевая гипотеза критерия Стьюдента при проверке значимости коэффициентов регрессии имеет вид:
| 
| 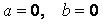 ++
++
| 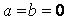
| 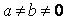
| 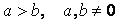
~Альтернативная гипотеза критерия Стьюдента при проверке значимости коэффициентов регрессии имеет вид:
| 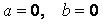
|  ++
++
| 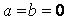
| 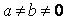
| 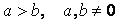
~Проверка значимости уравнения регрессии проводится с помощью критерия:
| Фишера
|Пирсона
|Стьюдента
|Манна-Уитни
|Колмогорова-Смирнова
~При проверке значимости уравнения регрессии определяется:
| 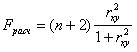
| 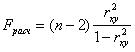 ++
++
| 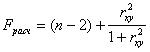
| 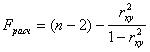
| 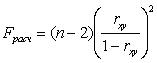
~Коэффициент детерминации принимает значения в промежутке:
|[-1; 1]
|[-1; 0]
|[0; 1]
|[-10; 10]
|[1; 10]
~Коэффициент … показывает, какая доля признака «у» учтена в анализе и вызвана влиянием на нее факторов, включенных в анализ.
|
|
|


