 |
|Крускала-Уоллиса. |рангов. |χ2-Пирсона. |Ж. Кювье. |корреляционный. |Чеддока. |прямую и обратную. |прямая . |обратная
|
|
|
|
|Крускала-Уоллиса
|Манна-Уитни
|Пирсона
|Фишера
|Колмогорова-Смирнова
~Непараметрический критерий, используемый для сравнения трех и более независимых групп:
| Крускала-Уоллиса
|Манна-Уитни
|Пирсона
|Фишера
|Колмогорова-Смирнова
~Критерий Крускала-Уоллиса рассчитывается с помощью:
|частот
|рангов
|вариантов
|дисперсии
|среднего
~Критерий Крускала-Уоллиса асимптотически приближается к распределению:
|t-Стьюдента
|F-Фишера
|χ 2-Пирсона
|Ф-Лапласа
|W-Уилкоксона
~ При критерии Крускала-Уоллиса проверяется нулевая гипотеза о:
|равенстве среднего некоторому значению
|равенстве дисперсий
|равенстве средних
|различии средних
|различии дисперсий
Вид нулевой гипотезы «Н0» критерия Крускала-Уоллиса:
| 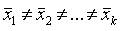
|  ++
++
| 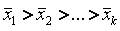
| 
| 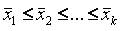
~ Вид альтернативной гипотезы «Н1» критерия Крускала-Уоллиса имеет вид:
| 
| 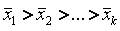
| 
| 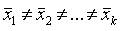 +++
+++
| 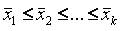
~Формула критерия Крускала-Уоллиса:
| 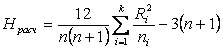
~При двухфакторном дисперсионном анализе формулируется … пары гипотез.
|3
|4
|2
|1
|5
~Для количественной оценки факторов риска развития заболевания используется … анализ.
|регрессионный
|дискриминантный
|кластерный
|корреляционный
|дисперсионный
~Термин «корреляция» ввел:
|Ф. Гальтон
|К. Пирсон
|Р. Фишер
|Ж. Кювье
|Ч. Дарвин
~В статистике термин «корреляция» первым стал использовать:
|Ж. Кювье +
|К. Пирсон
|Ф. Гальтон
|Р. Фишер
|Ч. Дарвин
~Количественный метод определения тесноты и направления связи между двумя и более случайными величинами - это... анализ.
|регрессионный
|дискриминантный
|кластерный
|дисперсионный
|корреляционный
~Показатель, характеризующий силу связи и ее направление:
|
|
|
|коэффициент детерминации
|ошибка аппроксимации
|коэффициент вариации
|коэффициент корреляции+
|размах вариации
~Коэффициент корреляции характеризует:
| силу и направление связи между признаками
|степень разброса случайной величины от ее среднего значения
|разность между максимальным и минимальным значениями признака
|среднее отклонение расчетных значений от фактических
|среднее значение случайной величины
~ Для оценки силы связи в теории корреляции применяется шкала:
|Чеддока
|Спирмена
|Пирсона
|Фишера
|Стьюдента
~Линейный коэффициент корреляции принимает значения в промежутке:
|[-1, 1]
|[0, 1]
|[-1, 0]
|[0, 10]
|[-10, 0]
~По направлению корреляционную связь различают:
|прямую и обратную
|сильную и слабую
|первичную и вторичную
|абсолютную и относительную
|зависимую и независимую
~Корреляционная связь, при которой увеличение среднего значения одной переменной влечет увеличение среднего значения другой переменной:
|обратная
|сильная
|прямая
|слабая
|умеренная
~ Корреляционная связь, при которой увеличение среднего значения одной переменной влечет уменьшение среднего значения другой переменной:
|прямая
|сильная
|обратная
|слабая
|умеренная
~При прямой связи коэффициент корреляции принимает значения:
|от -1 до 0
|от -1 до 1
|от -10 до 10
|от 0 до 1
|от 0 до 10
~При обратной связи коэффициент корреляции принимает значения:
|от 0 до 1
|от -1 до 1
|от -10 до 10
|от -1 до 0
|от 0 до 10
~Если коэффициент корреляции равен 0, то связь между явлениями:
|присутствует
|частичная
|отсутствует
|функциональная
|обратная
~Если коэффициент корреляции равен «+1» или «–1», то связь между явлениями:
|функциональная
|отсутствует
|присутствует
|частичная
|обратная
~Если 0, 1< rxy< 0, 3, то связь:
|
|
|


