 |
Основные свойства пределов.
|
|
|
|
Программный объем темы
1. Предел, непрерывность функции, основные свойства пределов, бесконечно малые и бесконечно большие. Замечательные пределы. Сравнение бесконечно малых. Эквивалентные бесконечно малые. Вычисление пределов с различными видами неопределенностей.
2. Определение производной, ее геометрический и механический смысл. Непрерывность и дифференцируемость. Основные правила нахождения производных. Дифференциал функции. Производные и дифференциалы высших порядков.
3. Применение пределов и производных к исследованию функций и построению их графиков. Правило Лопиталя и его применение к вычислению пределов.
3.1. ВВЕДЕНИЕ В АНАЛИЗ
Пусть функция f (x) определена в окрестности некоторой точки х = а,за исключением, быть может, самой точки а.
Определение (на языке « »). Число А называется пределом функции f(x) при
»). Число А называется пределом функции f(x) при  ,если для любого
,если для любого  >0 можно указать такое
>0 можно указать такое  > 0, что для всех х, удовлетворяющих соотношениям
> 0, что для всех х, удовлетворяющих соотношениям  , имеет место неравенство
, имеет место неравенство  .
.
Тот факт, что А есть предел f(х) при  , записывают в виде
, записывают в виде 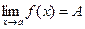 .
.
Если х<а (х > а) и  , то пишут
, то пишут  –0 (
–0 ( +0). В первом случае говорят, что X стремится к а слева, во втором случае – справа.
+0). В первом случае говорят, что X стремится к а слева, во втором случае – справа.
Определение (на языке « »). Число A называется пределом функции f(х) при
»). Число A называется пределом функции f(х) при  –0, если для любого
–0, если для любого  > 0 найдется такое
> 0 найдется такое  > 0, что для всех X, удовлетворяющих соотношениям
> 0, что для всех X, удовлетворяющих соотношениям  ,имеет место неравенство
,имеет место неравенство  .
.
Аналогично определяется предел функции f(х) при  справа. Тот факт, что функция f(х) при
справа. Тот факт, что функция f(х) при  слева и справа имеет своими пределами числа А –и A +;записывают в виде
слева и справа имеет своими пределами числа А –и A +;записывают в виде  ,
,  .
.
Данные пределы обозначают также символами f (а –0), f (а +0).
Пусть функция f(х) определена для всех х, достаточно больших по абсолютной величине ( ).
).
Определение (на языке « »). Число А называется пределом функции f(x) при
»). Число А называется пределом функции f(x) при  , если для любого
, если для любого  > 0 можно указать число М (М>К), такое, что для всех | х | > М выполняется неравенство
> 0 можно указать число М (М>К), такое, что для всех | х | > М выполняется неравенство  .
.
|
|
|
Обозначение:  .Подобным образом вводятся пределы при
.Подобным образом вводятся пределы при  ,
,  .
.
По аналогии со случаями конечных пределов (А - конечно) можно ввести пределы:
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
Например,  обозначает, что при любом заданном отрицательном числе N существует такое число M >0,что f (x)< N, если x > M.
обозначает, что при любом заданном отрицательном числе N существует такое число M >0,что f (x)< N, если x > M.
Основные свойства пределов.
Пусть 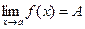 ,
,  , где А и В - конечные числа.
, где А и В - конечные числа.
Тогда
1.  ,
,
2. 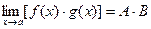 ,
,
3.  (при условии, что
(при условии, что 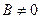 ).
).
При решении задач полезно помнить таблицу простейших пределов:
 ,
,  ,
,
 ,
,  ,
,
 ,
, 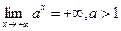 ,
,
 ,
, 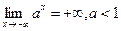 ,
,
 ,
, 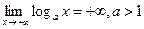 .
.
В таблице а>0,  .
.
Технически проще всего находится предел элементарной функции f(x)при 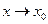 , если x0 принадлежит области определения этой функции. Такой предел равен f(x0). Ниже приведены основные положения, объясняющие этот результат.
, если x0 принадлежит области определения этой функции. Такой предел равен f(x0). Ниже приведены основные положения, объясняющие этот результат.
Определение. Класс функций, включающий в себя многочлены, рациональные функции, показательные, степенные, логарифмические, тригонометрические и обратные тригонометрические функции, а также функции, получающиеся из перечисленных с помощью четырех арифметических действий и суперпозиций (образование сложной функции), примененных конечное число раз, называют элементарными функциями.
Например,  ,
,  ,
, 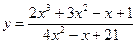 , y=tglncos3x2 принадлежат к классу элементарных функций.
, y=tglncos3x2 принадлежат к классу элементарных функций.
Теорема. Любая элементарная функция непрерывна в каждой точке своей области определения.
Теорема. Под знаком непрерывной в данной точке Х0 функции f(х) возможен предельный переход в этой точке:  .
.
Пример. 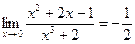 .
.
При вычислении пределов необходимо уметь раскрывать (решать) неопределенности.
Определение. Выражения вида  ,
,  ,
, 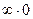 ,
, 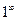 ,
, 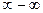 принято называть неопределенностями и обозначать, заключая в квадратные скобки:
принято называть неопределенностями и обозначать, заключая в квадратные скобки: 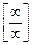 ,
,  ,
, 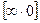 ,
, 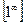 ,
, 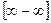 .
.
Далее на примерах рассматриваются приемы раскрытия основных типов неопределенностей.
При отыскании предела отношения двух целых многочленов относительно хпри  полезно предварительно разделить оба члена отношения на хn, где п - наивысшая степень этих многочленов.
полезно предварительно разделить оба члена отношения на хn, где п - наивысшая степень этих многочленов.
|
|
|
Пример.

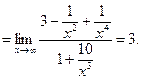
Пример.
 .
.
Пример.
 .
.
Пример.
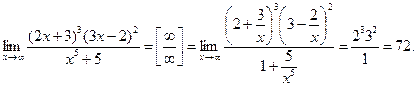
Аналогичный прием во многих случаях можно применять и для дробей, содержащих иррациональности.
Пример. 
Если P (x) и Q (x) – многочлены и P (a)= Q (a)=0, то при отыскании предела 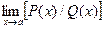 рекомендуется разделить один или несколько раз числитель и знаменатель на (x-a).
рекомендуется разделить один или несколько раз числитель и знаменатель на (x-a).
Пример.


Выражения, содержащие иррациональности, во многих случаях приводятся к рациональному виду путем введения новой переменной.
Пример. Найти 
Введем новую переменную 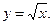
Тогда 
Другим приемом нахождения предела от иррационального выражения является перевод иррациональности из числителя в знаменатель или, наоборот, из знаменателя в числитель.
Пример. Найти 
Умножим числитель и знаменатель на выражение  , сопряженное с числителем.
, сопряженное с числителем.
Первый замечательный предел удобно представить в виде 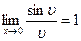 , где
, где  – функция независимой переменной x и
– функция независимой переменной x и  - при
- при  .
.
Первый замечательный предел может быть использован для раскрытия неопределенностей вида 
Пример. Найти предел 
Учитывая формулу  , находим:
, находим:
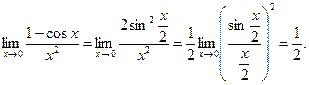
Пример. Найти предел 
Введем новую переменную z: z =arcsin2 x. Тогда sin z =2 x, 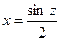 и
и 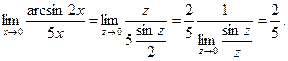
Второй замечательный предел запишем в виде  , если
, если  при
при  ; или
; или 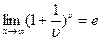 , если
, если  при
при  . Здесь
. Здесь  – функция независимой переменной x. Полезно также помнить пределы
– функция независимой переменной x. Полезно также помнить пределы  ,
, 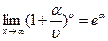 , где
, где 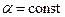 .
.
Второй замечательный предел может быть использован для раскрытия неопределенности 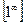 .
.
Пример. 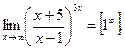
Используем известный прием деления «уголком» многочлена x +5 на многочлен x -1.

Значит,  .
.

Пример. Найти 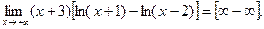
Учитывая свойства логарифмов, находим

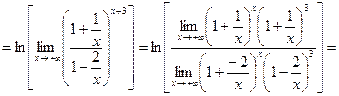

Замечание. Если существует и положителен 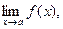 то
то 
Полезно также помнить и другие замечательные пределы.



Пример. 
Введя замену переменной y =cos2 x, находим:
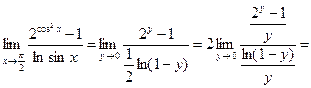

Пример. 


Определение.
Функция  называется бесконечно малой при
называется бесконечно малой при  , если
, если 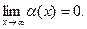
Пусть  и
и  являются бесконечно малыми функциями при
являются бесконечно малыми функциями при  . Если при этом их отношение стремится к единице
. Если при этом их отношение стремится к единице  , то бесконечно малые
, то бесконечно малые  и
и  называют эквивалентными малыми и пишут
называют эквивалентными малыми и пишут  ~
~  (
( ).
).
Примеры эквивалентных бесконечно малых функций при  :
:


m =const.
При отыскании предела отношения двух бесконечно малых функций каждую из них можно заменить эквивалентной бесконечно малой функцией.
|
|
|
Пример. 

Пример. 
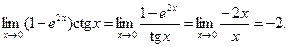
3.2. Дифференциальное исчисление функции
одной переменной
Определение. Предел отношения приращения функции  к приращению аргумента
к приращению аргумента  при произвольном стремлении
при произвольном стремлении  к нулю называется производной функции y = f (x) в точке x и обозначается одним из следующих символов: y ’, f ’(x),
к нулю называется производной функции y = f (x) в точке x и обозначается одним из следующих символов: y ’, f ’(x),  .
.

Если указанный в формуле (1) предел существует, то функцию f(x) называют дифференцируемой в точке x, а операцию нахождения производной y’ – дифференцированием.
Пример. Найти производную функции 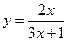 , воспользовавшись определением производной.
, воспользовавшись определением производной.
Решение. При любом приращении D х имеем:



Так как 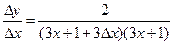 , то
, то

Справедливы следующие правила дифференцирования, где С –постоянное число, U(x) и V(x) –некоторые дифференцируемые функции.
1. (C)’=0;
2. (x)’=1;
3. (U 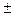 V)= U ’
V)= U ’ 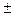 V ’;
V ’;
4. (C × U)’= C × U ’;
5. (U × V)’= U ’× V + U × V ’;
6.  ;
;
7. 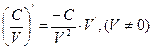 .
.
8. Если 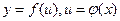 , т.е.
, т.е.  – сложная функция, составленная из дифференцируемых функций, то
– сложная функция, составленная из дифференцируемых функций, то
 или
или 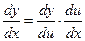 ;
;
9. Если для функции 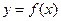 существует обратная дифференцируемая функция,
существует обратная дифференцируемая функция,  и
и 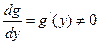 , то
, то  .
.
На основании определения производной и правил дифференцирования можно составить таблицу производных основных элементарных функций:
1.  ; 2.
; 2. 
3.  4.
4. 
5.  6.
6. 
7. 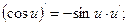 8.
8. 
9.  10.
10. 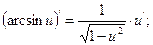
11.  12.
12. 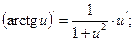
13.  14.
14. 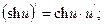
15.  16.
16. 
17. 
Примеры.
а) 



б) 


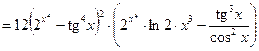
Если зависимость между переменными y и x задана в неявном виде f (x, y)=0, то для нахождения производной в простейших случаях достаточно продифференцировать обе части уравнения f (x, y)=0, y, считая функцией от x, и из полученного уравнения, линейного относительно  , найти производную.
, найти производную.
Логарифмической производной функции y=f (x) называется производная от логарифма этой функции, т.е.

Последовательное применение логарифмирования и дифференцирования функций называют логарифмическим дифференцированием.
Пример. Найти производную функцию  , если
, если

Решение. Дифференцируем обе части данного уравнения, считая y функцией от x:



Пример. Найти производную функции 
Решение. Логарифмируя данную функцию, получаем

Дифференцируя обе части последнего равенства по x,

отсюда



Производной второго порядка или второй производной функции y=f (x) называется производная от ее первой производной, т.е.  .
.
|
|
|
Обозначается вторая производная одним из следующих символов: 
Производной n –го порядка функции y=f (x) называется производная от производной (n–1)–го порядка данной функции.
Если зависимость функции y от аргумента x задана в параметрическом виде уравнениями x=x(t), y=y(t), то: 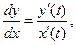
 где штрих обозначает производную по t.
где штрих обозначает производную по t.
Пример. Найти производную второго порядка функции 
Решение.

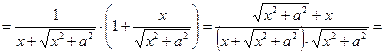


Пример. Найти производную функции, заданной параметрическими уравнениями: x=lnt, 
Решение.

Геометрически производная функции f(x) в т. x0 равна тангенсу угла наклона касательной, проведенной к графику функции в точке с абсциссой x0 с положительным направлением оси О x.
 .
.
Так как  называется угловым коэффициентом касательной, то можно записать
называется угловым коэффициентом касательной, то можно записать  , т.е.
, т.е.  Тогда уравнение касательной, как уравнение прямой, проходящей через т.
Тогда уравнение касательной, как уравнение прямой, проходящей через т.  с угловым коэффициентом
с угловым коэффициентом 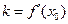 , может быть записано в виде
, может быть записано в виде  .
.
Пример. Составить уравнение касательной к гиперболе 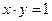 в т.
в т.  .
.
Решение. Здесь  ,
, 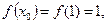

 Подставим найденные значения в уравнение касательной
Подставим найденные значения в уравнение касательной 
 .
.
Уравнение нормали (перпендикуляра) к кривой 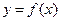 в точке
в точке  имеет вид
имеет вид 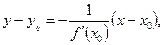
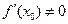 (если
(если 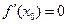 , уравнение нормали имеет вид
, уравнение нормали имеет вид  ).
).
Пример. Записать уравнение нормали к кривой 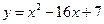 в т. с абсциссой x=1.
в т. с абсциссой x=1.
Решение. 


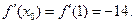
Тогда 

Рассмотрим применение производной к вычислению некоторых пределов.
Правило Лопиталя.
Пусть функции  и
и  непрерывны и дифференцируемы на некотором отрезке
непрерывны и дифференцируемы на некотором отрезке  и обращаются в нуль в т.
и обращаются в нуль в т.  , т.е.
, т.е.  , тогда, если существует предел отношения
, тогда, если существует предел отношения  при
при  , то существует и
, то существует и 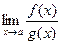 , причем
, причем  .
.
Пример. 
При необходимости это правило может быть применено многократно.
Пример. 
Правило Лопиталя применимо и для раскрытия неопределенностей вида 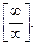
Пример. 
Пусть тело движется по прямой по закону  . За промежуток времени
. За промежуток времени  (от момента
(от момента  до момента
до момента  ) оно пройдет некоторый путь
) оно пройдет некоторый путь  . Тогда отношение
. Тогда отношение  есть средняя скорость движения за промежуток времени
есть средняя скорость движения за промежуток времени  .
.
Скоростью движения тела в данный момент времени  называется предел отношения приращения пути
называется предел отношения приращения пути  к приращению времени
к приращению времени  , когда приращение времени стремится к нулю:
, когда приращение времени стремится к нулю:

Следовательно, производная пути  по времени
по времени  равна скорости прямолинейного движения тела в данный момент времени
равна скорости прямолинейного движения тела в данный момент времени  :
:

Скорость протекания физических, химических и других процессов также выражается с помощью производной.
Рассмотрим произвольную функцию 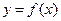 . Дадим
. Дадим 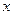 приращение
приращение  , тогда приращение функции равно
, тогда приращение функции равно  Отношение
Отношение  - называется средней скоростью изменения этой функции на отрезке
- называется средней скоростью изменения этой функции на отрезке  .
.
Скоростью изменения функции 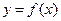 в точке
в точке 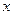 называется предел отношения приращения функции
называется предел отношения приращения функции  к приращению аргумента
к приращению аргумента  , когда приращение аргумента стремится к нулю:
, когда приращение аргумента стремится к нулю:
|
|
|

Итак, скорость изменения функции в точке 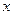 равна производной функции в этой точке.
равна производной функции в этой точке.
Если тело движется прямолинейно по закону  , то вторая производная пути
, то вторая производная пути  по времени
по времени  равна ускорению движения тела в данный момент времени
равна ускорению движения тела в данный момент времени  :
:

Таким образом, первая производная характеризует скорость некоторого процесса, а вторая - ускорение того же процесса.
Пусть функция 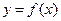 непрерывна при рассматриваемых значениях
непрерывна при рассматриваемых значениях 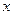 и имеет производную
и имеет производную

Из этого следует, что 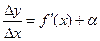 , где
, где  - бесконечно малая величина при
- бесконечно малая величина при  . Отсюда находим, что
. Отсюда находим, что 
Дифференциалом функции 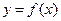 называется главная часть ее приращения, линейная относительно приращения
называется главная часть ее приращения, линейная относительно приращения  независимой переменной.
независимой переменной.
I. Дифференциал функции 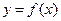 обозначается
обозначается  .
.
Итак, 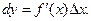
Положив  , получим
, получим  , и поэтому
, и поэтому

При достаточно малом  приращение функции приближенно равно ее дифференциалу,
приращение функции приближенно равно ее дифференциалу, 
Таким образом, 
Эта формула позволяет использовать дифференциал функции для приближенных вычислений значений функций.
|
|
|


